Giải Toán 8 trang 66 Tập 1 (Chân trời sáng tạo)

Với giải SGK Toán 8 Chân trời sáng tạo trang 66 chi tiết trong Bài 2: Tứ giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Nội dung bài viết

Thực hành 2 trang 66 Toán 8 Tập 1
Vận dụng 2 trang 66 Toán 8 Tập 1
Bài 1 trang 66 Toán 8 Tập 1
Bài 2 trang 66 Toán 8 Tập 1

Giải Toán 8 trang 66 Tập 1 (Chân trời sáng tạo)

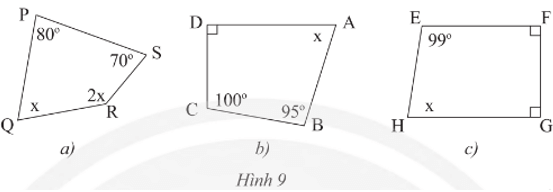
Thực hành 2 trang 66 Toán 8 Tập 1: Tìm x trong mỗi tứ giác sau:

Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác (ảnh 9)

Lời giải:

• Hình 9a):

Xét tứ giác PQRS có: 80° + 70° + 2x + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra 3x = 360° – (80° + 70°) = 210°

Do đó x = 70°.

• Hình 9b):

Xét tứ giác ABCD có: x + 95° + 100° + 90° = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (95° + 100° + 90°) = 75°.

• Hình 9c):

Xét tứ giác EFGH có: 99° + 90° + 90° + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (99° + 90° + 90°) = 81°.

Vận dụng 2 trang 66 Toán 8 Tập 1: Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

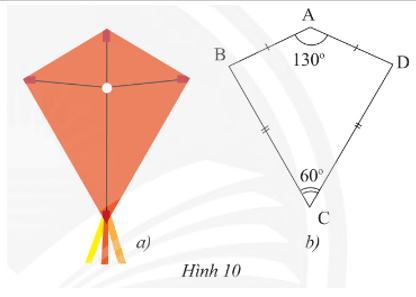
Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác (ảnh 10)

Lời giải:

Vận dụng 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\hat{B} = \hat{D}$ (hai góc tương ứng).

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $130 ° + \hat{B} + 60 ° + \hat{B} = 360 °$

Hay $2 \hat{B} = 360 ° - (130 ° + 60 °) = 170 °$ .

Do đó $\hat{B} = 85 °$ .

Vậy $\hat{B} = \hat{D} = 85 °$ .

Bài tập

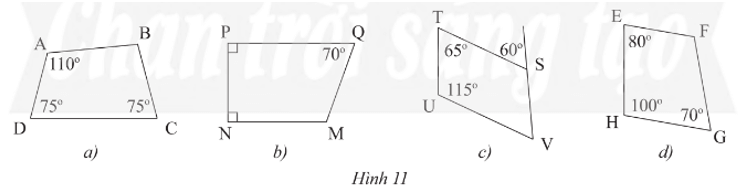
Bài 1 trang 66 Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác (ảnh 12)

Lời giải:

• Hình 11a):

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{B} = 360 ° - (\hat{A} + \hat{C} + \hat{D})$

Hay $\hat{B} = 360 ° - (110 ° + 75 ° + 75 °) = 100 °$ .

• Hình 11b):

Xét tứ giác MNPQ có: $\hat{M} + \hat{N} + \hat{P} + \hat{Q} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{M} = 360 ° - (\hat{N} + \hat{P} + \hat{Q})$

Hay $\hat{M} = 360 ° - (90 ° + 90 ° + 70 °) = 110 °$ .

• Hình 11c):

Ta có $\hat{T S V} = 180 ° - 60 ° = 120 °$ (do $\hat{T S V}$ kề bù với góc có số đo bằng 60°)

Xét tứ giác STUV có: $\hat{T S V} + \hat{T} + \hat{U} + \hat{V} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{V} = 360 ° - (\hat{T S V} + \hat{T} + \hat{U})$

Hay $\hat{V} = 360 ° - (120 ° + 65 ° + 115 °) = 60 °$ .

• Hình 11d):

Xét tứ giác EFGH có: $\hat{E} + \hat{F} + \hat{G} + \hat{H} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{F} = 360 ° - (\hat{E} + \hat{G} + \hat{H})$

Hay $\hat{F} = 360 ° - (80 ° + 70 ° + 100 °) = 110 °$ .

Bài 2 trang 66 Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

Hãy tính tổng số đo bốn góc ngoài của tứ giác ABCD ở Hình 12.

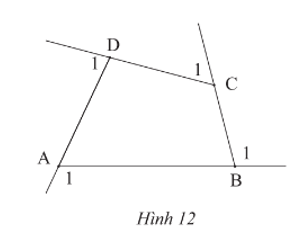
Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác (ảnh 13)

Lời giải:

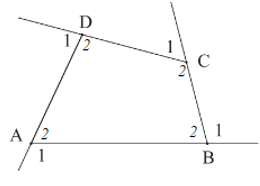
Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác (ảnh 14)

Xét tứ giác ABCD có: ${\hat{A}}_{2} + {\hat{B}}_{2} + {\hat{C}}_{2} + {\hat{D}}_{2} = 360 °$ (định lí tổng các góc của một tứ giác)

Mặt khác: ${\hat{A}}_{1} + {\hat{A}}_{2} = 180 °$ (hai góc kề bù)

Tương tự: ${\hat{B}}_{1} + {\hat{B}}_{2} = 180 °; {\hat{C}}_{1} + {\hat{C}}_{2} = 180 °; {\hat{D}}_{1} + {\hat{D}}_{2} = 180 °$

Suy ra

$({\hat{A}}_{1} + {\hat{A}}_{2}) + ({\hat{B}}_{1} + {\hat{B}}_{2}) + ({\hat{C}}_{1} + {\hat{C}}_{2}) + ({\hat{D}}_{1} + {\hat{D}}_{2}) = 180 ° + 180 ° + 180 ° + 180 °$