Với giải SGK Toán 11 Cánh Diều trang 47 chi tiết trong Bài 1: Dãy số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 47 Tập 1 (Cánh Diều)
Hoạt động 5 trang 47 Toán 11 Tập 1: Cho dãy số (un) với un = 1+ . Khẳng định un ≤ 2 với mọi n ∈ ℕ* có đúng không?
Lời giải:
Xét hiệu un – 2 = 1+ - 2 = -1
Vì n ∈ ℕ* nên n ≥ 1 suy ra ≤ 1 do đó: -1≤ 0 .
Vậy un – 2 ≤ 0 hay un ≤ 2.
Luyện tập 5 trang 47 Toán 11 Tập 1: Chứng minh rằng dãy số (un) với là bị chặn.
Lời giải:
Ta có: .
Ta lại có: >0
Do đó 0<.
Vì vậy dãy số (un) bị chặn.
Bài tập
Bài 1 trang 47 Toán 11 Tập 1: Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát un cho bởi công thức sau:
a) un = 2n2 + 1;
b) un = ;
c) un = ;
d) un = .
Lời giải:
a) Ta có: 5 số hạng đầu tiên của dãy (un) là: u1 = 2.12 + 1 = 3; u2 = 2.22 + 1 = 9; u3 = 2.32 + 1 = 19; u4 = 2.42 + 1 = 33; u5 = 2.52 + 1 = 51.
b) Ta có 5 số hạng đầu của dãy un = là:
c) Ta có 5 số hàng đầu của dãy un = là:
u1 = = 2 ; u2 = =4; u3 = = 8 ; u4 = = 16 ; u5 = = 32 .
d) Ta có 5 số hạng đầu của dãy un = là:
u1 = = 2; u2 = ; u3 = ; u4 = ; u5 = .
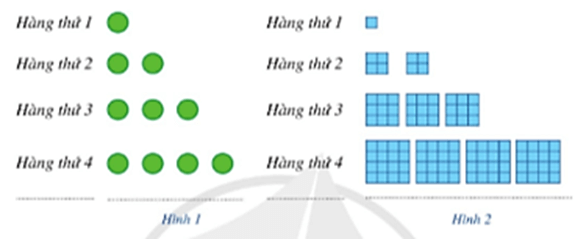
Bài 2 trang 47 Toán 11 Tập 1: a) Gọi un là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức số hạng tổng quát cho dãy số (un).
b) Gọi vn là tổng diện tích của các hình tô màu ở hàng thứ n trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số (vn).
Lời giải:
a) Số chấm ở hàng thứ nhất là: u1 = 1;
Số chấm ở hàng thứ hai là: u2 = 2;
Số chấm ở hàng thứ ba là: u3 = 3;
Số chấm ở hàng thứ tư là: u4 = 4;
Vậy số chấm ở hàng thứ n là: un = n.
b) Diện tích của các ô màu ở hàng thứ nhất là: v1 = 1 = 13;
Diện tích của các ô màu ở hàng thứ hai là: v2 = 8 = 23;
Diện tích của các ô màu ở hàng thứ ba là: v3 = 27 = 33;
Diện tích của các ô màu ở hàng thứ tư là: v4 = 64 = 43;
Vậy diện tích của các ô màu ở hàng thứ n là: vn = n3.
Xem thêm các bài giải Toán 11 Cánh Diều hay, chi tiết khác:
Câu hỏi khởi động trang 43 Toán 11 Tập 1: Một số loài hoa có số lượng cánh hoa luôn là một số cố định. Số cánh hoa trong các bông hoa thường xuất hiện nhiều theo những con số 1, 1, 2, 3, 5, 8, 13, 21,...
Hoạt động 1 trang 43 Toán 11 Tập 1: Một vật chuyển động đều với vận tốc 20 m/s. Hãy viết các số chỉ quãng đường (đơn vị: mét) vật chuyển động được lần lượt trong thời gian 1 giây, 2 giây, 3 giây, 4 giây, 5 giây theo hàng ngang.
Luyện tập 1 trang 44 Toán 11 Tập 1: Hàm số u(n) = n3 xác định trên tập hợp M = {1; 2; 3; 4; 5} là một dãy số hữu hạn. Tìm số hạng đầu, số hạng cuối và viết dãy số trên dưới dạng khai triển.
Hoạt động 2 trang 44 Toán 11 Tập 1: Cho hàm số u(n) = , n ∈ ℕ*. Hãy viết các số u1; u2; ...; un; ... theo hàng ngang.
Luyện tập 2 trang 44 Toán 11 Tập 1: Cho dãy số (un) = n2. a) Viết năm số hạng đầu và số hạng tổng quát của dãy số (un).
Hoạt động 3 trang 45 Toán 11 Tập 1: Xét mỗi dãy số sau: ● Dãy số: 1; 4; 9; 16; 25; 36; 49; 64; 81; 100 (1)
Luyện tập 3 trang 46 Toán 11 Tập 1: Cho dãy số (un) với . Tìm u33, u333 và viết dãy số dưới dạng khai triển.
Hoạt động 4 trang 46 Toán 11 Tập 1: Cho dãy số (un) với un = n2. Tính un+1. Từ đó, hãy so sánh un+1 và un với mọi n ∈ ℕ*.
Luyện tập 4 trang 46 Toán 11 Tập 1: Chứng minh rằng dãy số (vn) với vn = là một dãy số giảm.
Hoạt động 5 trang 47 Toán 11 Tập 1: Cho dãy số (un) với un = 1+ . Khẳng định un ≤ 2 với mọi n ∈ ℕ* có đúng không?
Luyện tập 5 trang 47 Toán 11 Tập 1: Chứng minh rằng dãy số (un) với là bị chặn.
Bài 1 trang 47 Toán 11 Tập 1: Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát un cho bởi công thức sau: un = 2n2 + 1;
Bài 2 trang 47 Toán 11 Tập 1: a) Gọi un là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức số hạng tổng quát cho dãy số (un).
Bài 3 trang 48 Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (un), biết:
a) ;
Bài 4 trang 48 Toán 11 Tập 1: Trong các dãy số (un) được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?
Bài 5 trang 48 Toán 11 Tập 1: Cho dãy số thực dương (un). Chứng minh rằng dãy số (un) là dãy số tăng khi và chỉ khi >1 với mọi n ∈ ℕ*.
Bài 6 trang 48 Toán 11 Tập 1: Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau. Lần đầu chị gửi 100 triệu động. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi Pn (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng.
