Toptailieu.vn giới thiệu Vở bài tập trang 127,128, 129, 130 Bài 6: Thể tích của hình lăng trụ đứng chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc
Vở bài tập trang 127,128, 129, 130 Bài 6: Thể tích của hình lăng trụ đứng
Câu hỏi Vở bài tập Toán 8 trang 127 - 130: Hình lăng trụ đứng tam giác có các cạnh bên, cạnh đáy đều bằng nhau và có độ dài bằng (h.83).
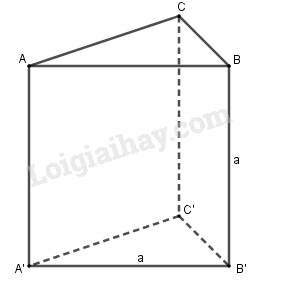
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng.
a) Với , thể tích của hình lăng trụ đứng (lấy đến chữ số thập phân) là:
A. B.
C. D.
b) Với , thể tích của hình lăng trụ đứng (lấy đến chữ số thập phân) là:
A. B.
C. D.
c) Với , thể tích của hình lăng trụ đứng (lấy đến chữ số thập phân) là:
A. B.
C. D.
Phương pháp giải: Sử dụng công thức tính thể tích hình lăng trụ đứng với là diện tích đáy, là chiều cao
Lời giải:
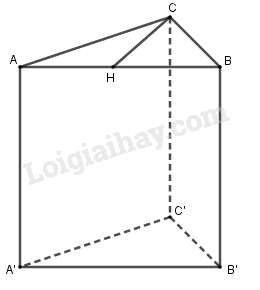
Kẻ .
đều nên là đường cao, đường trung tuyến.
Tam giác vuông tại có:
(Py-ta-go)
.
Diện tích tam giác là:
.
Thể tích hình lăng trụ đứng là:
.
a) Với , thể tích hình lăng trụ đứng là:
Chọn A.
b) Với , thể tích hình lăng trụ đứng là:
Chọn B.
c) Với , thể tích hình lăng trụ đứng là:
Chọn C.
Vở bài tập Toán 8 trang 127 - 130 Bài 21:
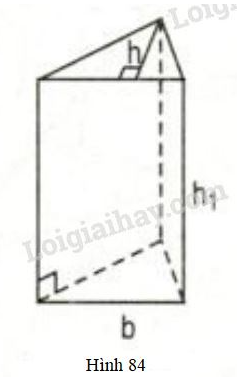
Quan sát hình 84 rồi điền số thích hợp vào các ô bảng sau:
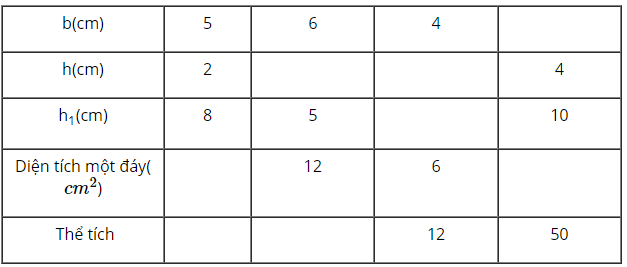
Phương pháp giải:
Áp dụng các công thức :
Thế tích: , trong đó là diện tích đáy, là chiều cao hình lăng trụ
Diện tích đáy : với là chiều cao ứng với cạnh đáy
Lời giải:
Ta có : Diện tích đáy: .
Thể tích
+ Ở cột 2 :
+ Ở cột 3 :
+ Ở cột 4:
+ Ở cột 5:
Vậy có kết quả sau khi điền vào bảng sau là:
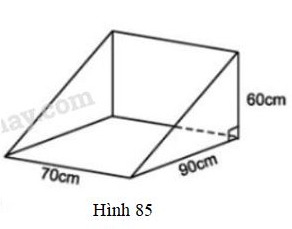
Vở bài tập Toán 8 trang 127 - 130 Bài 22:Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác (h.85). Hãy tính dung tích của thùng
Phương pháp giải:
Áp dụng công thức :
Thể tích lăng trụ: , trong đó là diện tích đáy, là chiều cao lăng trụ.
Đáy là tam giác vuông nên diện tích đáy : , trong đó là độ dài hai cạnh góc vuông.
Lời giải:
Thùng đựng là lăng trụ đứng tam giác. Đáy là tam giác vuông có hai cạnh góc vuông là và . Chiều cao của lăng trụ đứng là .
Vậy dung tích của thùng là:
.
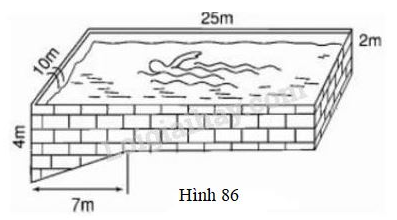
Vở bài tập Toán 8 trang 127 - 130 Bài 23: Các kích thước của một bể bơi được cho trên hình 86 ( mặt nước có dạng hình chữ nhật ). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước ?
Phương pháp giải:
- Bể bơi được chia thành hai phần: phần hình hộp chữ nhật với các kích thước là và phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là và chiều cao .
- Tính thể tích hình hộp chữ nhật: , trong đó là các kích thước của hình hộp chữ nhật.
- Thể tích lăng trụ: , trong đó là diện tích đáy, là chiều cao.
Lời giải:
Khi tháo hết nước đi, bể bơi có dạng như hình 86. Bể bơi gồm hai phần:
- Phần nông là một hình hộp chữ nhật có các kích thước là và .
- Phần nước sâu là một lăng trụ đứng tam giác có đáy là tam giác vuông với hai cạnh góc vuông là và , đường cao là (chiều rộng của bể bơi).
Do đó ta có:
Thể tích hình hộp chữ nhật
Thể tích hình lăng trụ đứng
Khi đầy ắp nước trong bể, số mét khối nước là:
.
Vở bài tập Toán 8 trang 127 - 130 Bài 24: Điền số thích hợp vào các ô trống ở bảng sau:
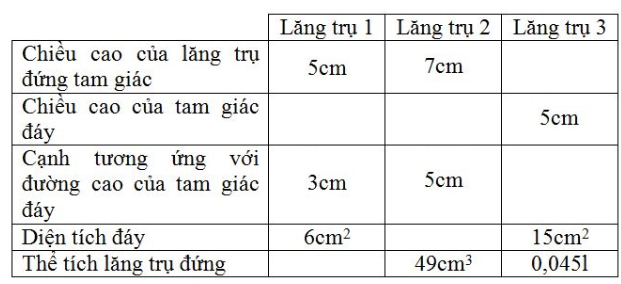
Phương pháp giải:
+) và ;
+) và ,
Trong đó là thể tích của lăng trụ, là diện tích đáy, là chiều cao của lăng trụ đứng tam giác, là chiều cao của tam giác đáy, là cạnh tương ứng với đường cao của tam giác đáy.
Lời giải:
Với là thể tích của lăng trụ, là diện tích đáy, là chiều cao của lăng trụ đứng tam giác, là chiều cao của tam giác đáy, là cạnh tương ứng với đường cao của tam giác đáy.
+) Lăng trụ 1 :
+) Lăng trụ 2:
+) Lăng trụ 3:
Ta có
Điền vào bảng, ta được kết quả sau:
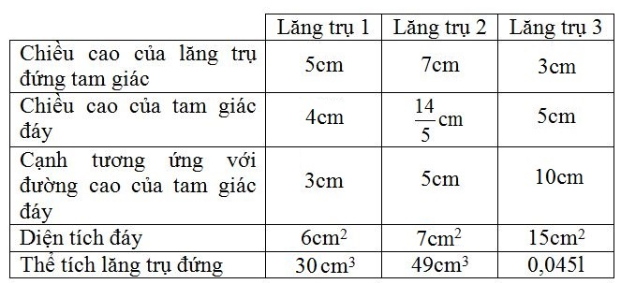
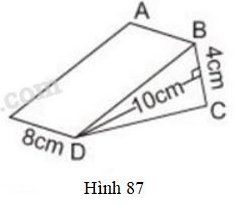
Vở bài tập Toán 8 trang 127 - 130 Bài 25: Hình 87 biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng, là một tam giác cân.
Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết:
a) song song với những cạnh nào?
b) Tính thể tích lưỡi rìu?
c) Tính khối lượng của lưỡi rìu, biết khối lượng riêng của sắt là (phần cán gỗ bên trong lưỡi rìu là không đáng kể).
Phương pháp giải:
- Thể tích lăng trụ , trong đó là diện tích đáy, là chiều cao lăng trụ.
- Khối lượng lưỡi rìu = khối lượng riêng thể tích lưỡi rìu.
Lời giải:
a, Vẽ nét khuất vào hình rồi điền chữ vào các đỉnh , ta có:
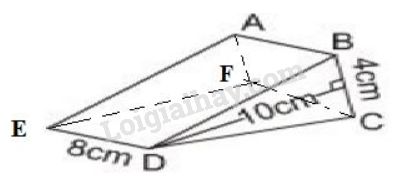
Trong , .
Trong , .
b) Thể tích của lưỡi rìu là:
c) Khối lượng của lưỡi rìu là:
Vở bài tập Toán 8 trang 127 - 130 Bài 26: Hình 88 là một lăng trụ đứng, đáy là hình thang vuông.
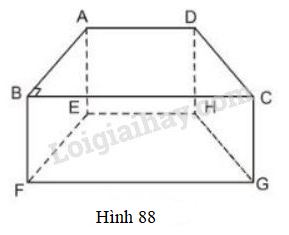
Hãy kể tên:
a) Các cạnh song song với cạnh .
b) Cạnh song song với
c) Các đường thẳng song song với mặt phẳng
d) Các đường thẳng song song với mặt phẳng .
Phương pháp giải: Dựa vào tính chất của hình lăng trụ đứng và giả thiết đề bài cho đáy là hình thang vuông.
Lời giải:
a) Các cạnh song song với là: .
b) Các cạnh song song với là: .
c) Các đường thẳng song song với mặt phẳng là: và .
d) Các đường thẳng song song với mặt phẳng là: .




