Toptailieu.vn biên soạn và giới thiệu Bất phương trình logarit: Phương pháp giải và bài tập hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Bất phương trình logarit , từ đó học tốt môn Toán.

Bất phương trình logarit: Phương pháp giải và bài tập hay, chi tiết

I. LÝ THUYẾT

1. Định nghĩa

Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.

2. Phương trình và bất phương trình lôgarit cơ bản: cho a,  b>0,  a≠1

Bất phương trình lôgarit cơ bản có dạng:  

logaf(x)>b;  logaf(x)≥b;  logaf(x)<b;  logaf(x)≤blogaf(x)>b;logaf(x)≥b;logaf(x)<b;logaf(x)≤b

3. Phương pháp giải phương trình và bất phương trình lôgarit

+ Đưa về cùng cơ số

Nếu a>1 thì logaf(x)>logag(x)

⇔{g(x)>0f(x)>g(x)

Nếu 0<a<1 thì logaf(x)>logag(x)

⇔{f(x)>0f(x)<g(x)

+ Đặt ẩn phụ

+ Mũ hóa

+ Phương pháp hàm số và đánh giá

II. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Bất phương trình logarit cơ bản

A. Phương pháp giải

Ta có BPT

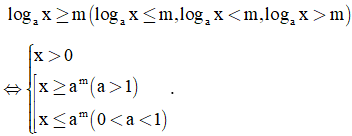
B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình ${\log }_3\left({\log }_{\frac{1}{2}}x\right)<1$ là:

A. $\left(0;1\right).$

B. $\left(\frac{1}{8};1\right).$

C. $\left(1;8\right).$

D. $\left(\frac{1}{8};3\right).$

Hướng dẫn giải

$$\begin{gathered} {\log }_3\left({\log }_{\frac{1}{2}}x\right)<1\iff 0<{\log }_{\frac{1}{2}}x<3 \\ \iff 1>x>{\left(\frac{1}{2}\right)}^3\iff \frac{1}{8}<x<1 \end{gathered}$$

Vậy tập nghiệm của BPT $\left(\frac{1}{8};1\right).$

Chọn B.

Câu 2: Bất phương trình ${\log }_2\left(x^2-2x+3\right)>1$ có tập nghiệm là

A. $ℝ\backslash \left\{1\right\}$

B. $ℝ$

C. $\left\{1\right\}$

D. $\varnothing$

Hướng dẫn giải

Chọn A.

$$\begin{gathered} {\log }_2\left(x^2-2x+3\right)>1 \\ \iff x^2-2x+3>2^1 \\ \iff x^2-2x+1>0 \\ \iff {\left(x-1\right)}^2>0\iff x\ne 1 \end{gathered}$$

Vậy tập nghiệm $S=ℝ\backslash \left\{1\right\}$

Câu 3: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left(2x-1\right)>-1$ là:

A. $\left(1;\frac{3}{2}\right)$

B. $\left(\frac{3}{2};+\infty \right)$

C. $\left(\frac{1}{2};\frac{3}{2}\right)$

D. $\left(-\infty ;\frac{3}{2}\right)$

Hướng dẫn giải

Chọn C.

Ta có:

$$\begin{gathered} {\log }_{\frac{1}{2}}\left(2x-1\right)>-1 \\ \iff \left\{\begin{array}{c}2x-1<2\\ 2x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{c}x<\frac{3}{2}\\ x>\frac{1}{2}\end{array}\right.\iff \frac{1}{2}<x<\frac{3}{2}. \end{gathered}$$

Vậy tập nghiệm của BPT là: $S=\left(\frac{1}{2};\frac{3}{2}\right)$

Câu 4: Điều kiện xác định của bất phương trình $\ln \frac{x^2-1}{x}<0$ là:

A. $\left[\begin{array}{l}-1<x<0\\ x>1\end{array}\right.$

B. $x>-1$

C. $x>0$

D. $\left[\begin{array}{l}x<-1\\ x>1\end{array}\right.$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện:

$\frac{x^2-1}{x}>0\iff \left[\begin{array}{l}-1<x<0\\ x>1\end{array}\right.$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính $\ln \frac{X^2-1}{X}$

Nhấn CALC và cho $X=-0,5$ (thuộc đáp án A và B) máy tính hiển thị 0,4054651081. Vậy loại đáp án C và  D.

Nhấn CALC và cho $X=0,5$(thuộc đáp án B) máy tính không tính được. Vậy loại B,

Chọn A.

Câu 5: Bất phương trình ${\log }_{\frac{2}{3}}\left(2x^2-x+1\right)<0$ có tập nghiệm là:

A. $S=\left(0;\frac{3}{2}\right)$

B. $S=\left(-1;\frac{3}{2}\right)$

C. $S=\left(-\infty ;0\right)\cup \left(\frac{1}{2};+\infty \right)$

D. $S=\left(-\infty ;1\right)\cup \left(\frac{3}{2};+\infty \right)$

Hướng dẫn giải

[Phương pháp tự luận]

$$\begin{gathered} {\log }_{\frac{2}{3}}\left(2x^2-x+1\right)<0 \\ \iff 2x^2-x+1>1\iff \left[\begin{array}{l}x<0\\ x>\frac{1}{2}\end{array}\right. \end{gathered}$$

Vậy tập nghiệm của BPT $S=\left(-\infty ;0\right)\cup \left(\frac{1}{2};+\infty \right)$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính ${\log }_{\frac{2}{3}}\left(2X^2-X+1\right)$

Nhấn CALC và cho $X=-5$ (thuộc đáp án A và D) máy tính hiển thị – 9,9277….

Vậy loại đáp án A và B.

Nhấn CALC và cho $X=1$ (thuộc đáp án C) máy tính hiển thị – 1,709511291.

Chọn C.

Câu 6: Tập nghiệm của bất phương trình ${\log }_3\frac{4x+6}{x}\le 0$ là:

A. $S=\left[-2;-\frac{3}{2}\right)$

B. $S=\left[-2;0\right)$

C. $S=\left(-\infty ;2\right]$

D. $S=ℝ\backslash \left[-\frac{3}{2};0\right]$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

$$\begin{gathered} {\log }_3\frac{4\text{x}+6}{x}\le 0\iff \left\{\begin{array}{l}\frac{4\text{x}+6}{x}>0\\ \frac{4\text{x}+6}{x}\le 1\end{array}\right. \\ \iff \left\{\begin{array}{l}x<-\frac{3}{2}\vee x>0\\ -2\le x<0\end{array}\right. \\ \iff -2\le x<-\frac{3}{2} \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left[-2;-\frac{3}{2}\right)$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính ${\log }_3\frac{4X+6}{X}$

Nhấn CALC và cho $X=1$ (thuộc đáp án C và D) máy tính hiển thị 2,095903274. Vậy loại đáp án C và D.

Nhấn CALC và cho $X=-1$ (thuộc đáp án B) máy tính không tính được. Vậy loại B

Dạng 2. Phương pháp đưa về cùng cơ số

A. Phương pháp giải

Xét bất phương trình ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$ $(a>0,a\ne 1)$

Nếu $a>1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)>g\left(x\right)$ (cùng chiều khi a > 1)

Nếu $0<a<1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)<g\left(x\right)$ (ngược chiều khi $0<a<1$)

Nếu a chứa ẩn thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff \left\{\begin{array}{l}f\left(x\right)>0;g\left(x\right)>0\\ (a-1)\left[f\left(x\right)-g\left(x\right)\right]>0\end{array}\right.$(hoặc chia 2 trường hợp của cơ số)

B. Ví dụ minh họa

Câu 1: Điều kiện xác định của bất phương trình ${\log }_{\frac{1}{2}}(4x+2)-{\log }_{\frac{1}{2}}(x-1)>lo{g}_{\frac{1}{2}}x$ là:

A. $x>-\frac{1}{2}$

B. $x>0$

C. $x>1$

D. $x>-1$

Hướng dẫn giải

Chọn C.

BPT xác định khi:

$$\begin{gathered} \left\{\begin{array}{l}x>0\\ 4x+2>0\\ x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>0\\ x>-\frac{1}{2}\\ x>1\end{array}\right.\iff x>1 \end{gathered}$$

Câu 2: Điều kiện xác định của bất phương trình ${\log }_2(x+1)-2{\log }_4(5-x)<1-{\log }_2(x-2)$ là:

A. $2<x<5$

B. $1<x<2$

C. $2<x<3$

D. $-4<x<3$

Hướng dẫn giải

Chọn A.

BPT xác định khi:

$$\begin{gathered} \left\{\begin{array}{l}x+1>0\\ 5-x>0\\ x-2>0\end{array}\right.\iff \left\{\begin{array}{l}x>-1\\ x<5\\ x>2\end{array}\right. \\ \iff 2<x<5 \end{gathered}$$

Câu 3: Điều kiện xác định của bất phương trình ${\log }_5(x-2)+{\log }_{\frac{1}{5}}(x+2)>{\log }_{5}x-3$ là:

A. $x>3$

B. $x>2$

C. $x>-2$

D. $x>0$

Hướng dẫn giải

Chọn B.

[Phương pháp tự luận]

Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}x-2>0\\ x+2>0\\ x>0\end{array}\right.\iff \left\{\begin{array}{l}x>2\\ x>-2\\ x>0\end{array}\right. \\ \iff x>2 \end{gathered}$$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_5(X-2)+{\log }_{\frac{1}{5}}(X+2)-{\log }_{5}X+3$

Nhấn CALC và cho $X=1$ máy tính không tính được. Vậy loại đáp án C và D.

Nhấn CALC và cho $X=\frac{5}{2}$(thuộc đáp án B) máy tính hiển thị 1,065464369.

Câu 4: Điều kiện xác định của bất phương trình ${\log }_{0,5}(5\text{x}+15)\le {\log }_{0,5}\left(x^2+6\text{x}+8\right)$ là:

A. $x>-2$

B. $\left[\begin{array}{l}x<-4\\ x>-2\end{array}\right.$

C. $x>-3$

D. $-4<x<-2$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}5x+15>0\\ x^2+6\text{x}+8>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>-3\\ \left[\begin{array}{l}x>-2\\ x<-4\end{array}\right.\end{array}\right. \\ \iff x>-2 \end{gathered}$$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{0,5}(5X+15)-{\log }_{0,5}(X^2+6\text{X}+8)$

Nhấn CALC và cho $X=-3,5$ máy tính không tính được. Vậy loại đáp án C và  D.

Nhấn CALC và cho $X=-5$ (thuộc đáp án B) máy tính không tính được.

Vậy loại B,

Chọn A.

Câu 5: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\left(x^2-6x+5\right)+{\log }_3\left(x-1\right)\ge 0$ là:

A. $S=\left[1;6\right]$

B. $S=\left(5;6\right]$

C. $S=\left(5;+\infty \right)$

D. $S=\left(1;+\infty \right)$

Hướng dẫn giải

[Phương pháp tự luận]

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{\frac{1}{3}}\left(X^2-6\text{X}+5\right)+{\log }_3\left(X-1\right)$

Nhấn CALC và cho $X=2$ (thuộc đáp án A và D) máy tính không tính được. Vậy loại đáp án A và D.

Nhấn CALC và cho $X=7$ (thuộc đáp án C) máy tính hiển thị – 0,6309297536.

Vậy loại C,

Chọn B.

Câu 6: Nghiệm nguyên nhỏ nhất của bất phương trình ${\log }_{0,2}x-{\log }_5\left(x-2\right)<{\log }_{0,2}3$ là:

A. $x=6$

B. $x=3$

C. $x=5$

D. $x=4$

Hướng dẫn giải

[Phương pháp tự luận]

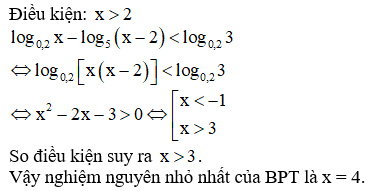
[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{0,2}X-{\log }_5\left(X-2\right)-{\log }_{0,2}3$

Nhấn CALC và cho $X=3$  (nhỏ nhất) máy tính hiển thị 0. Vậy loại đáp án B.

Nhấn CALC và cho $X=4$ máy tính hiển thị -0.6094234797.

Chọn D.

Dạng 3. Phương pháp đặt ẩn phụ

A. Phương pháp giải

Tương tự với phương pháp giải phương trình logarit bằng phương pháp đặt ẩn phụ nhưng lưu ý tới chiều biến thiên của hàm số.

B. Ví dụ minh họa

Câu 1 : Nghiệm nguyên lớn nhất của bất phương trình ${\log }_2^{4}x-{\log }_{\frac{1}{2}}^2\left(\frac{x^3}{8}\right)+9{\log }_2\left(\frac{32}{x^2}\right)<4{\log }_{2^{-1}}^2\left(x\right)$ là:

A. $x=7$

B. $x=8$

C. $x=4$

D. $x=1$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

Điều kiện: x >0

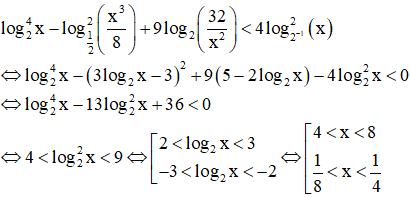
Vậy giá trị nguyên lớn nhất của x thỏa mãn ĐK trên là: x = 7.

[Phương pháp trắc nghiệm]

Lần lượt thay $x=7;x=8;x=4;x=1$ thấy $x=7$ đúng.

Câu 2: Bất phương trình ${\log }_{0,2}^{2}x-5{\log }_{0,2}x<-6$ có tập nghiệm là:

A. $S=\left(\frac{1}{125};\frac{1}{25}\right)$

B. $S=\left(2;3\right)$

C. $S=\left(0;\frac{1}{25}\right)$

D. $S=\left(0;3\right)$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

Điều kiện: $x>0$

$$\begin{gathered} {\log }_{0,2}^2-5{\log }_{0,2}x<-6 \\ \iff 2<{\log }_{0,2}x<3 \\ \iff \frac{1}{125}<x<\frac{1}{25} \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left(\frac{1}{125};\frac{1}{25}\right)$.

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\left({\log }_{0,2}^{}X\right)}^2-5{\log }_{0,2}X+6$

Nhấn CALC và cho $X=2,5$ (thuộc đáp án B và D) máy tính hiển thị 9.170746391. Vậy loại đáp án B và D.

Nhấn CALC và cho $X=\frac{1}{200}$ (thuộc đáp án C) máy tính hiển thị 0,3773110048.

Câu 3: Nghiệm nguyên nhỏ nhất của bất phương trình ${\log }_{x}3-{\log }_{\frac{x}{3}}3<0$ là:

A. x = 3

B. x =1

C. x =2

D. x =4

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện: $x>0;x\ne 1;x\ne 3$

$$\begin{gathered} {\log }_{x}3-{\log }_{\frac{x}{3}}3<0 \\ \iff \frac{-1}{{\log }_{3}x.\left({\log }_{3}x-1\right)}<0 \\ \iff \left[\begin{array}{l}{\log }_{3}x<0\\ {\log }_{3}x>1\end{array}\right.\iff \left[\begin{array}{l}0<x<1\\ x>3\end{array}\right. \end{gathered}$$

Vậy nghiệm nguyên nhỏ nhất của BPT là x = 4.

[Phương pháp trắc nghiệm]

Loại B, A vì $x\ne 1;x\ne 3$

Loại C vì $x=2\Rightarrow {\log }_{2}3-{\log }_{\frac{2}{3}}3>0$

Chọn D.

Câu 4: Nếu đặt $t={\log }_3\frac{x-1}{x+1}$ thì bất phương trình ${\log }_4{\log }_3\frac{x-1}{x+1}<{\log }_{\frac{1}{4}}{\log }_{\frac{1}{3}}\frac{x+1}{x-1}$ trở thành bất phương trình nào?

A. $\frac{t^2-1}{t}<0$

B. $t^2-1<0$

C. $\frac{t^2-1}{t}>0$

D. $\frac{t^2+1}{t}<0$

Hướng dẫn giải

Điều kiện: $x\in (-\infty ;-1)\cup (1;+\infty )$

Sau khi đưa về cùng cơ số 4, rồi tiếp tục biến đổi về cùng cơ số 3 ta được bất phương trình

${\log }_3\frac{x-1}{x+1}-\frac{1}{{\log }_3\frac{x-1}{x+1}}<0$

Chọn A.

Dạng 4. Phương pháp mũ hóa

A. Phương pháp giải

Tương tự với giải phương trình logarit bằng phương pháp mũ hóa.

B. Ví dụ minh họa

Câu 1: Bất phương trình ${\log }_x\left({\log }_3\left(9^x-72\right)\right)\le 1$ có tập nghiệm là:

A. $S=\left[{\log }_3\sqrt{73};2\right]$

B. $S=\left({\log }_3\sqrt{72};2\right]$

C. $S=\left({\log }_3\sqrt{73};2\right]$

D. $S=\left(-\infty ;2\right]$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện $x>{\log }_3\sqrt{73}$

$$\begin{gathered} {\log }_x\left({\log }_3\left(9^x-72\right)\right)\le 1 \\ \iff {\log }_3\left(9^x-72\right)\le x \\ \iff 9^x-3^x-72\le 0 \\ \iff 3^x\le 9\iff x\le 2 \end{gathered}$$

Kết hợp với điều kiện ${\log }_3\sqrt{73}<x\le 2$

Vậy tập nghiệm của BPT là: $S=\left({\log }_3\sqrt{73};2\right]$

Chọn A.

[Phương pháp trắc nghiệm]

Thay $x={\log }_3\sqrt{73}$ (thuộc B, C, D) vào biểu thức ${\log }_x\left({\log }_3\left(9^x-72\right)\right)$ được ${\log }_x\left(0\right)$ không xác định, vậy loại B, C, D.

 Chọn A.

Câu 2: Điều kiện xác định của phương trình ${\log }_2\left[3{\log }_2\left(3x-1\right)-1\right]=x$ là:

A. $x>\frac{\sqrt[3]{2}+1}{3}$

B.  $x\ge \frac{1}{3}$

C. $x>0$

D. $x\in (0;+\infty )\backslash \text{{}1\}$

Hướng dẫn giải

[Phương pháp tự luận]

Biểu thức ${\log }_2\left[3{\log }_2\left(3x-1\right)-1\right]=x$ xác định khi và chỉ khi:

$$\begin{gathered} \left\{\begin{array}{l}3{\log }_2\left(3x-1\right)-1>0\\ 3x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}{\log }_2\left(3x-1\right)>\frac{1}{3}\\ x>\frac{1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}3x-1>2^{\frac{1}{3}}\\ x>\frac{1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x>\frac{2^{\frac{1}{3}}+1}{3}\\ x>\frac{1}{3}\end{array}\right. \\ \iff x>\frac{2^{\frac{1}{3}}+1}{3} \end{gathered}$$

[Phương pháp trắc nghiệm]

Thay $x=\frac{1}{3}$ (thuộc B, C, D) vào biểu thức ${\log }_2\left(3x-1\right)$ được ${\log }_2\left(0\right)$ không xác định, vậy loại B, C, D.

Chọn A.

Câu 3: Nghiệm nguyên lớn nhất của bất phương trình ${\log }_3\left({4.3}^{x-1}\right)>2x-1$ là:

A. $x=3$

B. $x=2$

C. $x=1$

D. $x=-1$

Hướng dẫn giải

[Phương pháp tự luận]

$$\begin{gathered} {\log }_3\left({4.3}^{x-1}\right)>2x-1 \\ \iff {4.3}^{x-1}>3^{2x-1} \\ \iff 3^{2x}-{4.3}^x<0 \\ \iff 0<3^x<4\iff x<{\log }_{3}4 \end{gathered}$$

Vậy nghiệm nguyên lớn nhất của BPT là: x = 1.

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_3\left({4.3}^{X-1}\right)-2X+1$

Nhấn CALC và cho $X=3$ (lớn nhất) máy tính hiển thị –1.738140493. Vậy loại đáp án    A.

Nhấn CALC và cho $X=2$ máy tính hiển thị – 0.7381404929. Vậy loại B.

Nhấn CALC và cho $X=1$ máy tính hiển thị 0.2618595071.

Chọn C.

Dạng 5. Phương pháp hàm số, đánh giá

A. Phương pháp giải

Cho hàm số $y=f\left(t\right)$ xác định và liên tục trên D:

Nếu hàm số $f\left(t\right)$ luôn đồng biến trên D và $\forall u,v\in D$ thì $f\left(u\right)>f\left(v\right)\iff u>v$

Nếu hàm số $f\left(t\right)$ luôn nghịch biến trên D và $\forall u,v\in D$ thì $f\left(u\right)>f\left(v\right)\iff u<v$

B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình ${\log }_2\left(x^2-4x+16\right)-{\log }_2\left(x\right)\le -5x^2+40x-74$ là:

A. $\left(-4;4\right)$

B. $\left(4;+\infty \right)$

C. $\left\{4\right\}$

D. $\left(-\infty ;4\right)$

Hướng dẫn giải

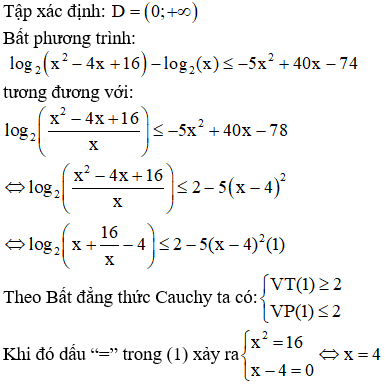
So với điều kiện xác định ta nhận nghiệm x= 4

So bốn đáp án, chỉ có đáp án C thỏa mãn.

Chọn C.

Câu 2: Cho bất phương trình ${\log }_2\left(\frac{x^2+2x+3}{x^2+3x+2}\right)\le -2x+2$. Phát biểu nào sau đây là Sai:

A. Bất phương trình đã cho có tập nghiệm là $T=\left(-\infty ;-2\right)\cup \left(\left.-1;1\right]\right.$

B. Bất phương trình đã cho có tập nghiệm là $T=\left(-\infty ;0\right)\cup \left(1;+\infty \right)$

C. Tập xác định của phương trình đã cho là $\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

D. Bất phương trình đã cho không có nghiệm nguyên.

Hướng dẫn giải

Bất phương trình :

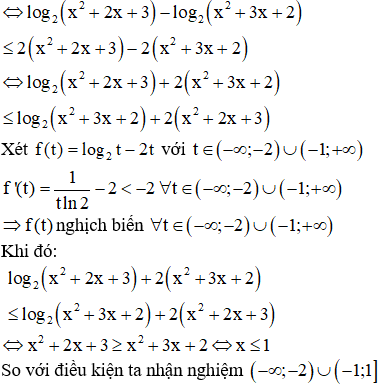
Chọn B.

Câu 3: Bất phương trình ${\log }_2(2^x+1)+{\log }_3(4^x+2)\le 2$ có tập nghiệm là:

A. $\text{[}0;+\infty )$

B. $(-\infty ;0)$

C. $(-\infty ;0]$

D. $\left(0;+\infty \right)$

Hướng dẫn giải

Chọn C.

Xét:

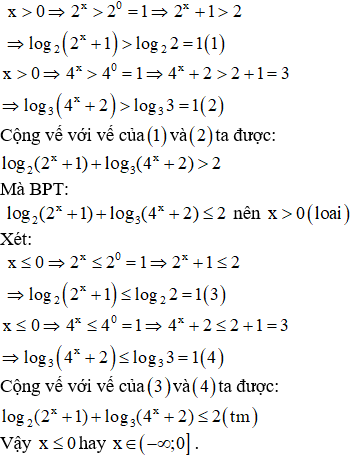
III. BÀI TẬP TỰ LUYỆN

Câu 1: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}{x}^2\ge -1$ là

A.  $\left[\sqrt{2};+\infty \right).$

B.  $\left[-\sqrt{2};0\right)\cup \left(0;\sqrt{2}\right].$

C.  $\left[-\sqrt{2};\sqrt{2}\right].$

D. $\left(0;\sqrt{2}\right].$

Câu 2: Tìm tập nghiệm S của bất phương trình: ${\log }_{\frac{1}{2}}\frac{2}{x-1}>2$

A. $S=\left(1;1+\sqrt{2}\right)$

B. $S=\left(1;9\right)$

C. $S=\left(1+\sqrt{2};+\infty \right)$

D. $S=\left(9;+\infty \right)$

Câu 3: Tìm tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left(x^2-3x+2\right)\ge -1$

A. $\left(-\infty ;1\right)$

B. $\left[0;1\right)\cup \left(2;3\right]$

C. $\left[0;2\right)\cup \left(3;7\right]$

D. $\left[0;2\right)$

Câu 4: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left(x-1\right)\ge 0$ là:

A. $\left(1;2\right)$

B. $\left(1;2\right]$

C. $\left(-\infty ;2\right]$

D. $\left[2;+\infty \right)$

Câu 5: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left({\log }_2\left(2x-1\right)\right)>0$ là:

A. $S=\left(1;\frac{3}{2}\right)$

B. $S=\left(0;\frac{3}{2}\right)$

C. $S=\left(0;1\right)$

D. $S=\left(\frac{3}{2};2\right)$

Câu 6: Tập nghiệm của bất phương trình ${\log }_2(x^2-3x+1)\le 0$ là:

A. $S=\left[0;\frac{3-\sqrt{5}}{2}\right)\cup \left(\frac{3+\sqrt{5}}{2};3\right]$

B. $S=\left(0;\frac{3-\sqrt{5}}{2}\right)\cup \left(\frac{3+\sqrt{5}}{2};3\right)$

C. $S=\left[\frac{3-\sqrt{5}}{2};\frac{3+\sqrt{5}}{2}\right]$

D. $S=\varnothing$

Câu 7: Tìm số nghiệm nguyên của bất phương trình ${\log }_{\sqrt{3}-1}\left(x^2-2x+1\right)>0.$

A. Vô số.

B. 0

C. 2

D. 1

Câu 8: Điều kiện xác định của bất phương trình ${\log }_{\frac{1}{2}}\left[{\log }_2(2-x^2)\right]>0$ là:

A. $x\in \text{[}-1;1]$

B. $x\in \left(-1;0\right)\cup \left(0;1\right)$

C. $x\in \left(-1;1\right)\cup \left(2;+\infty \right)$

D. $x\in \left(-1;1\right)$

Câu 9: Tìm tất cả các giá trị thực của tham số m để bất phương trình ${\log }_2(5^x-1)\le m$ có nghiệm $x\ge 1$?

A. $m\ge 2$

B. $m>2$

C. $m\le 2$

D. $m<2$

Câu 10: Tìm tất cả các giá trị thực của tham số m để phương trình  ${\log }_2\left(mx-x^2\right)=2$ vô nghiệm?

A. $m<4$

B. $-4<m<4$

C. $\left[\begin{array}{l}m>4\\ m<-4\end{array}\right.$

D. $m>-4$

Câu 11: Bất phương trình ${\log }_2\left(x^2-x-2\right)\ge {\log }_{0,5}\left(x-1\right)+1$ có tập nghiệm là:

A. $S=\left[1-\sqrt{2};+\infty \right)$

B. $S=\left[1+\sqrt{2};+\infty \right)$

C. $S=\left(-\infty ;1+\sqrt{2}\right]$

D. $S=\left(-\infty ;1-\sqrt{2}\right]$.

Câu 12: Tập nghiệm của bất phương trình ${\log }_4\left(2x^2+3x+1\right)>{\log }_2\left(2x+1\right)$ là:

A. $S=\left(\frac{1}{2};1\right)$

B. $S=\left(0;\frac{1}{2}\right)$

C. $S=\left(-\frac{1}{2};1\right)$

D. $S=\left(-\frac{1}{2};0\right)$

Câu 13: Bất phương trình ${\log }_{\frac{3}{4}}(2x+1)\ge {\log }_{\frac{3}{4}}(x+2)$ có tập nghiệm S là

A. $S=\left(-\frac{1}{2};1\right]$

B. $S=\left(-2;1\right)$

C. $S=\left[-\frac{1}{2};1\right]$

D. $S=\left(-\frac{1}{2};1\right)$

Câu 14: Xác định tập nghiệm S của bất phương trình $\ln x^2>\ln (4x-4)$

A. $S=\left(1;+\infty \right)\backslash \left\{2\right\}.$

B. $S=ℝ\backslash \left\{2\right\}.$

C. $S=\left(2;+\infty \right).$

D. $S=\left(1;+\infty \right).$

Câu 15: Tập nghiệm của bất phương trình $\log \left(x^2+25\right)>\log \left(10x\right)$ là

A. $\left(0;+\infty \right)$

B. $ℝ\backslash \left\{5\right\}$

C. $\left(0;5\right)\cup \left(5;+\infty \right)$

D. R.

Câu 16: Tìm tập nghiệm S của bất phương trình ${\log }_{\frac{1}{2}}\left(x+1\right)<{\log }_{\frac{1}{2}}\left(2x-1\right)$

A. $S=\left(2;+\infty \right)$

B. $S=\left(-\infty ;2\right)$

C. $S=\left(\frac{1}{2};2\right)$

D. $S=\left(-1;2\right)$

Câu 17: Tập nghiệm của bất phương trình ${\log }_{0,8}\left(x^2+x\right)<{\log }_{0,8}\left(-2x+4\right)$ là:

A. $\left(1;2\right)$

B. $\left(-\infty ;-4\right)\cup \left(1;2\right)$

C. $\left(-\infty ;-4\right)\cup \left(1;+\infty \right)$

D. $\left(-4;1\right)$

Câu 18: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\left(x^2-2x+1\right)<{\log }_{\frac{1}{3}}\left(x-1\right)$ là

A. $\left(3;+\infty \right).$

B.  $\left(1;+\infty \right).$

C.  $\left(1;2\right).$

D. $\left(2;+\infty \right).$

Câu 19: Nghiệm của bất phương trình ${\log }_2{x}^2+{\log }_{\frac{1}{2}}\left(x+2\right)<{\log }_2\left(2x+3\right)$ là

A. $x<-\frac{3}{2}$

B. $x>-\frac{3}{2}$

C. $-1<x<0$ hoặc $x>0$.

D. $-\frac{3}{2}<x\le -1$

Câu 20: Tìm tập nghiệm của bất phương trình ${\log }_2{x}^2+{\log }_{\frac{1}{2}}\left(x+2\right)\ge {\log }_{\sqrt{2}}\left(2x+3\right)$

A. $S=\left(-\frac{3}{2};-1\right]$

B. $S=\left(-\infty ;-\frac{3}{2}\right]$

C. $S=\left[-1;+\infty \right)$

D. $S=\left(-\frac{3}{2};+\infty \right)$

Câu 21: Tìm m để bất phương trình $1+{\log }_5\left(x^2+1\right)\ge {\log }_5\left(m{x}^2+4x+m\right)$ thoã mãn với mọi $x\in ℝ$

A. $-1<m\le 0$

B. $-1<m<0$

C. $2<m\le 3$

D. $2<m<3$

Câu 22: Tập nghiệm của bất phương trình $\left({16}^x-4^{x+1}-5\right)\cdot {\log }_4\left(4x-1\right)+{\log }_{\frac{1}{2}}32<{16}^{\frac{x+1}{2}}-{16}^x$ là:

A. $\left(\frac{1}{4};+\infty \right)$

B. $\left(\frac{5}{16};{\log }_{4}5\right)$

C. $\left(\frac{1}{4};{\log }_{4}5\right)\backslash \left\{\frac{5}{16}\right\}$

D.  $\left(\frac{1}{4};\frac{5}{16}\right)$

Câu 23: Tập nghiệm của bất phương trình $\left(9^x-3\cdot 3^x-4\right)\cdot {\log }_3\left(2x-1\right)+{\log }_{\frac{1}{3}}81<9^{\frac{x+1}{2}}-9^x$là:

A. $\left(\frac{1}{2};{\log }_{3}4\right)\backslash \left\{\frac{2}{3}\right\}$

B. $\left(\frac{2}{3};{\log }_{3}4\right)$

C. $\left(\frac{1}{2};\frac{2}{3}\right)$

D.  $\left(\frac{1}{2};+\infty \right)$

Câu 24: Tập nghiệm của bất phương trình $\left(4^x-2^x-2\right){\log }_2\left(x-1\right)+{\log }_{\frac{1}{2}}4<2^x-4^x\left(1\right)$

A. $T=\left(1;+\infty \right)$

B. $T=\left(-\infty ;\frac{3}{2}\right)$

C. $T=\varnothing$

D.  $T=\left(1;\frac{3}{2}\right)$

Câu 25: Cho a là số nguyên dương lớn nhất thỏa mãn $3{\log }_3\left(1+\sqrt{a}+\sqrt[3]{a}\right)>2{\log }_2\sqrt{a}$. Tìm phần nguyên của ${\log }_2\left(2017a\right)$.

A. 14.

B. 22.

C. 16.

D. 19.

ĐÁP ÁN

Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Phương trình lôgarit và cách giải các dạng bài tập

Bất phương trình mũ và cách giải các dạng bài tập

Các dạng toán về lãi suất ngân hàng và cách giải

Công thức lũy thừa đầy đủ, chi tiết nhất

Công thức logarit đầy đủ, chi tiết nhất