Toptailieu.vn biên soạn và giới thiệu lời Toán 11 (Kết nối tri thức) Bài 6: Cấp số cộng hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 11 Bài 6 từ đó học tốt môn Toán 11.

Toán 11 (Kết nối tri thức) Bài 6: Cấp số cộng

Giải Toán 11 trang 48

Mở đầu trang 48 Toán 11 Tập 1: Một nhà hát có 25 hàng ghế với 16 ghế ở hàng thứ nhất, 18 ghế ở hàng thứ hai, 20 ghế ở hàng thứ 3 và cứ tiếp tục theo quy luật đó, tức là hàng sau nhiều hơn hàng liền trước nó 2 ghế. Tính tổng số ghế của nhà hát đó.

Lời giải:

Sau bài học này ta sẽ giải quyết được bài toán trên như sau:

Số ghế ở mỗi hàng của nhà hát lập thành một cấp số cộng, gồm 25 số hạng, với số hạng đầu u₁ = 16 và công sai d = 2. Tổng các số hạng này là

S₂₅ = u₁ + u₂ + ... + u₂₅ = $\frac{25}{2}\left(2u_1+\left(25-1\right)d\right)=\frac{25}{2}\left(2.16+24.2\right)=1000$ .

Vậy nhà hát đó có tổng cộng 1 000 ghế.

1. Định nghĩa

HĐ1 trang 48 Toán 11 Tập 1: Cho dãy số (u­_n) gồm tất cả các số tự nhiên lẻ, xếp theo thứ tự tăng dần.

a) Viết năm số hạng đầu của dãy số.

b) Dự đoán công thức biểu diễn số hạng u_n theo số hạng u_{n – 1}.

Lời giải:

a) Năm số hạng đầu của dãy số (u_n) là năm số tự nhiên lẻ đầu tiên và đó là: 1; 3; 5; 7; 9.

b) Nhận thấy trong dãy số (u_n), số hạng sau hơn số hạng liền trước 2 đơn vị.

Do đó, ta dự đoán công thức biểu diễn số hạng u_n theo số hạng u_{n – 1} là u_n = u_{n – 1} + 2.

Câu hỏi trang 48 Toán 11 Tập 1: Dãy số không đổi a, a, a, ... có phải là một cấp số cộng không?

Lời giải:

Dãy số không đổi a, a, a, ... là một cấp số cộng với công sai d = 0.

2. Số hạng tổng quát

Giải Toán 11 trang 49

Luyện tập 1 trang 49 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = – 2n + 3. Chứng minh rằng (u_n) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này.

Lời giải:

Ta có: u_{n – 1} = – 2(n – 1) + 3 = – 2n + 2 + 3 = – 2n + 5

Do đó, u_n – u_{n – 1} = (– 2n + 3) – (– 2n + 5) = – 2, với mọi n ≥ 2.

Vậy dãy số (u_n) là cấp số cộng có số hạng đầu là u₁ = – 2 . 1 + 3 = 1 và công sai d = – 2.

HĐ2 trang 49 Toán 11 Tập 1: Cho cấp số cộng (u_n) với số hạng đầu u₁ và công sai d.

a) Tính các số hạng u₂, u₃, u₄, u₅ theo u₁ và d.

b) Dự đoán công thức tính số hạng tổng quát u_n theo u₁ và d.

Lời giải:

a) Ta có: u₂ = u₁ + d;

u₃ = u₂ + d = (u₁ + d) + d = u₁ + 2d;

u₄ = u₃ + d = (u₁ + 2d) + d = u₁ + 3d;

u₅ = u₄ + d = (u₁ + 3d) + d = u₁ + 4d.

b)Từ câu a, ta dự đoán công thức tính số hạng tổng quát u_n theo u₁ và d là

u_n = u₁ + (n – 1)d.

Luyện tập 2 trang 49 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = 4n – 3. Chứng minh rằng (u_n) là một cấp số cộng. Xác định số hạng đầu u₁ và công sai d của của cấp số cộng này. Từ đó viết số hạng tổng quát u_n­ dưới dạng u_n = u₁ + (n – 1)d.

Lời giải:

Ta có: u_n – u_{n – 1} = (4n – 3) – [4(n – 1) – 3] = 4n – 3 – (4n – 4 – 3) = 4, với mọi n ≥ 2.

Do đó, dãy số (u_n) là một cấp số cộng với số hạng đầu u₁ = 4 . 1 – 3 = 1 và công sai d = 4.

Số hạng tổng quát là: u_n = 1 + (n – 1) . 4

3. Tổng n số hạng đầu của một cấp số cộng

Giải Toán 11 trang 50

HĐ3 trang 50 Toán 11 Tập 1: Cho cấp số cộng (u_n) với số hạng đầu u₁ và công sai d.

Để tính tổng của n số hạng đầu

S_n = u₁ + u₂ + ... + u_{n – 1} + u_n,

hãy lần lượt thực hiện các yêu cầu sau:

a) Biểu diễn mỗi số hạng trong tổng S_n theo số hạng đầu u₁ và công sai d.

b) Viết S_n theo thứ tự ngược lại: S_n = u_n + u_{n – 1} + ... + u₂ + u₁ và sử dụng kết quả ở phần a) để biểu diễn mỗi số hạng trong tổng này theo u₁ và d.

c) Cộng từng vế hai đẳng thức nhận được ở a), b), để tính S_n theo u₁ và d.

Lời giải:

a) Ta có: u₂ = u₁ + d; ...; u_{n – 1} = u₁ + (n – 1 – 1)d = u₁ + (n – 2)d; u_n = u₁ + (n – 1)d.

S_n = u₁ + u₂ + ... + u_{n – 1} + u_n

= u₁ + (u₁ + d) + ... + [u₁ + (n – 2)d] + [u₁ + (n – 1)d]

b) S_n = u_n + u_{n – 1} + ... + u₂ + u₁

= [u₁ + (n – 1)d] + [u₁ + (n – 2)d] + ... + (u₁ + d) + u₁

c) Ta có:

S_n + S_n = {u₁ + (u₁ + d) + ... + [u₁ + (n – 2)d] + [u₁ + (n – 1)d]} + {[u₁ + (n – 1)d] + [u₁ + (n – 2)d] + ... + (u₁ + d) + u₁}

⇔ 2S_n = {u₁ + [u₁ + (n – 1)d]} + {(u₁ + d) + [u₁ + (n – 2)d]} + ... + {[u₁ + (n – 2)d] + (u₁ + d)} + {[u₁ + (n – 1)d] + u₁}

⇔ 2S_n = [2u₁ + (n – 1)d] + [2u₁ + (n – 1)d] + ... + [2u₁ + (n – 1)d] + [2u₁ + (n – 1)d]

⇔ 2S­_n = n . [2u₁ + (n – 1)d]

⇔ S_n = [2u₁ + (n – 1)d] .

Vận dụng trang 50 Toán 11 Tập 1: Anh Nam được nhận vào làm việc ở một công ty về công nghệ với mức lương khởi điểm là 100 triệu đồng một năm. Công ty sẽ tăng thêm lương cho anh Nam mỗi năm là 20 triệu đồng. Tính tổng số tiền lương mà anh Nam nhận được sau 10 năm làm việc cho công ty đó.

Lời giải:

Số tiền lương anh Nam nhận được mỗi năm lập thành một cấp số cộng, gồm 10 số hạng, với số hạng đầu u₁ = 100 và công sai d = 20.

Tổng 10 số hạng đầu của cấp số cộng này là

S₁₀ = u₁ + u₂ + ... + u₁₀ = $\frac{10}{2}\left(2u_1+\left(10-1\right)d\right)=\frac{10}{2}\left(2.100+9.20\right)=1900$ .

Vậy số tiền lương mà anh Nam nhận được sau 10 năm làm việc ở công ty này là 1 900 triệu đồng hay 1 tỷ 900 triệu đồng.

Bài tập

Giải Toán 11 trang 51

Bài 2.8 trang 51 Toán 11 Tập 1: Xác định công sai, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số cộng sau:

a) 4, 9, 14, 19, ...;

b) 1, – 1, – 3, – 5, ....

Lời giải:

a) Ta có: công sai của cấp số cộng đã cho là d = 9 – 4 = 5.

Số hạng đầu của cấp số cộng là u₁ = 4.

Số hạng thứ 5 của cấp số cộng là u₅ = u₁ + (5 – 1)d = 4 + 4 . 5 = 24.

Số hạng tổng quát của cấp số cộng là

u_n = u₁ + (n – 1)d = 4 + (n – 1) . 5 = 4 + 5n – 5 = 5n – 1 hay u_n = 5n – 1.

Số hạng thứ 100 của cấp số cộng là u₁₀₀ = 5 . 100 – 1 = 499.

b) Ta có: công sai của cấp số cộng đã cho là d = – 1 – 1 = – 2.

Số hạng đầu của cấp số cộng là u₁ = 1.

Số hạng thứ 5 của cấp số cộng là u₅ = u₁ + (5 – 1)d = 1 + 4 . (– 2) = – 7.

Số hạng tổng quát của cấp số cộng là

u_n = u₁ + (n – 1)d = 1 + (n – 1) . (– 2) = 1 – 2n + 2 = – 2n + 3 hay u_n = – 2n + 3.

Số hạng thứ 100 của cấp số cộng là u₁₀₀ = (– 2) . 100 + 3 = – 197.

Bài 2.9 trang 51 Toán 11 Tập 1: Viết năm số hạng đầu của mỗi dãy số (u_n) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của nó dưới dạng u_n = u₁ + (n – 1)d.

a) u_n = 3 + 5n;

b) u_n = 6n – 4;

c) u₁ = 2, u_n = u_{n – 1} + n;

d) u₁ = 2, u_n = u_{n – 1} + 3.

Lời giải:

a) u_n = 3 + 5n

+) Năm số hạng đầu của dãy số (u_n) là:

u₁ = 3 + 5 . 1 = 8;

u₂ = 3 + 5 . 2 = 13;

u₃ = 3 + 5 . 3 = 18;

u₄ = 3 + 5 . 4 = 23;

u₅ = 3 + 5 . 5 = 28.

+) Ta có: u_n – u_{n – 1} = (3 + 5n) – [3 + 5(n – 1)] = 5, với mọi n ≥ 2.

Do đó dãy số (u_n) là một cấp số cộng với số hạng đầu u₁ = 8 và công sai d = 5.

Số hạng tổng quát của cấp số cộng này là u_n = u₁ + (n – 1)d = 8 + (n – 1). 5.

b) u_n = 6n – 4

+) Năm số hạng đầu của dãy số (u_n) là:

u₁ = 6 . 1 – 4 = 2;

u₂ = 6 . 2 – 4 = 8;

u₃ = 6 . 3 – 4 = 14;

u₄ = 6 . 4 – 4 = 20;

u₅ = 6 . 5 – 4 = 26.

+) Ta có: u_n – u_{n – 1} = (6n – 4) – [6(n – 1) – 4] = 6, với mọi n ≥ 2.

Do đó dãy số (u_n) là một cấp số cộng với số hạng đầu u₁ = 2 và công sai d = 6.

Số hạng tổng quát của cấp số cộng này là u_n = u₁ + (n – 1)d = 2 + (n – 1). 6.

c) u₁ = 2, u_n = u_{n – 1} + n

+) Năm số hạng đầu của dãy số (u_n) là:

u₁ = 2;

u₂ = u₁ + 2 = 2 + 2 = 4;

u₃ = u₂ + 3 = 4 + 3 = 7;

u₄ = u₃ + 4 = 7 + 4 = 11;

u₅ = u₄ + 5 = 11 + 5 = 16.

Ta có: u_n = u_{n – 1} + n ⇔ u_n – u_{n – 1} = n, do n luôn thay đổi nên hiệu hai số hạng liên tiếp của dãy số (u_n) thay đổi.

Vậy dãy số (u_n) không phải là cấp số cộng.

d) u₁ = 2, u_n = u_{n – 1} + 3

+) Năm số hạng đầu của dãy số (u_n) là:

u₁ = 2;

u₂ = u₁ + 3 = 2 + 3 = 5;

u₃ = u₂ + 3 = 5 + 3 = 8;

u₄ = u₃ + 3 = 8 + 3 = 11;

u₅ = u₄ + 3 = 11 + 3 = 14.

Ta có: u_n = u_{n – 1} + 3 ⇔ u_n – u_{n – 1} = 3, với mọi n ≥ 2.

Do đó dãy số (u_n) là một cấp số cộng với số hạng đầu u₁ = 2 và công sai d = 3.

Số hạng tổng quát của cấp số cộng này là u_n = u₁ + (n – 1)d = 2 + (n – 1). 3.

Bài 2.10 trang 51 Toán 11 Tập 1: Một cấp số cộng có số hạng thứ 5 bằng 18 và số hạng thứ 12 bằng 32. Tìm số hạng thứ 50 của cấp số cộng này.

Lời giải:

Ta biểu diễn số hạng thứ 5 và số hạng thứ 12 theo số hạng thứ nhất u₁ và công sai d.

Ta có: u₅ = u₁ + (5 – 1)d hay 18 = u₁ + 4d.

u₁₂ = u₁ + (12 – 1)d hay 32 = u₁ + 11d.

Khi đó ta có hệ phương trình  .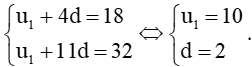

Số hạng thứ 50 của cấp số cộng là u₅₀ = u₁ + (50 – 1)d = 10 + 49 . 2 = 108.

Bài 2.11 trang 51 Toán 11 Tập 1: Một cấp số cộng có số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2 700?

Lời giải:

Cấp số cộng có u₁ = 5 và d = 2. Giả sử tổng của n số hạng đầu bằng 2 700. Khi đó ta có:

S_n = $\frac{n}{2}\left(2u_1+\left(n-1\right)d\right)=\frac{n}{2}\left(2.5+\left(n-1\right).2\right)=2700$ .

Do đó, $\frac{n}{2}\left(2.5+\left(n-1\right).2\right)=2700$

⇔ n(10 + 2n – 2) = 5 400

⇔ n(2n + 8) – 5 400 = 0

⇔ 2n² + 8n – 5 400 = 0

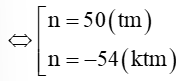
Vậy tổng của 50 số hạng đầu của cấp số cộng đã cho bằng 2 700.

Bài 2.12 trang 51 Toán 11 Tập 1: Giá của một chiếc xe ô tô lúc mới mua là 680 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc ô tô giảm 55 triệu đồng. Tính giá còn lại của chiếc xe sau 5 năm sử dụng.

Lời giải:

Giá của chiếc xe ô tô sau một năm sử dụng là 680 – 55 = 625 (triệu đồng)

Giá của chiếc xe ô tô sau mỗi năm sử dụng lập thành một cấp số cộng với số hạng đầu là u₁ = 625 và công sai d = – 55 (do giá xe giảm).

Do đó, giá của chiếc ô tô sau 5 năm sử dụng là

u₅ = u₁ + (5 – 1)d = 625 + 4 . (– 55) = – 405 (triệu đồng).

Bài 2.13 trang 51 Toán 11 Tập 1: Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba, và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với số ghế ở hàng liền kề trước nó). Nếu muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu bao nhiêu hàng ghế?

Lời giải:

Số ghế ở mỗi hàng của hội trường lập thành một cấp số cộng với số hạng đầu u₁ = 15 và công sai d = 3. Giả sử cần thiết kế tối thiếu n hàng ghế để hội trường có sức chứa ít nhất 870 ghế ngồi.

Ta có: S_n = $\frac{n}{2}\left(2u_1+\left(n-1\right)d\right)=\frac{n}{2}\left(2.15+\left(n-1\right).3\right)\ge 870$

Do đó, n(30 + 3n – 3) ≥ 1 740

⇔ n(3n + 27) – 17 40 ≥ 0

⇔ 3n² + 27n – 1 740 ≥ 0

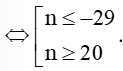
Vậy cần thiết kế tối thiểu 20 hàng ghế để thỏa mãn yêu cầu bài toán.

Bài 2.14 trang 51 Toán 11 Tập 1: Vào năm 2020, dân số của một thành phố là khoảng 1,2 triệu người. Giả sử mỗi năm, dân số của thành phố này tăng thêm khoảng 30 nghìn người. Hãy ước tính dân số của thành phố này vào năm 2030.

Lời giải:

Ta có: 1,2 triệu người = 1 200 nghìn người.

Dân số mỗi năm của thành phố từ năm 2020 đến năm 2030 lập thành một cấp số cộng, gồm 11 số hạng (2030 – 2020 + 1 = 11), với số hạng đầu u₁ = 1 200 và công sai d = 30.

Ta có: u₁₁ = u₁ + (11 – 1)d = 1 200 + 10 . 30 = 1 500.

Vậy dân số của thành phố này vào năm 2030 khoảng 1 500 nghìn người hay 1,5 triệu người.

Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 1

Bài 5: Dãy số

Bài 7: Cấp số nhân

Bài tập cuối chương 2

Bài 8: Mẫu số liệu ghép nhóm