Với giải Hoạt động 4 trang 30 Chuyên đề Toán lớp 11 Cánh Diều chi tiết trong Bài 2: Phép đồng dạng giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
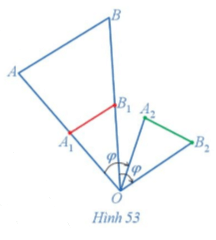
Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng: Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB
Hoạt động 4 trang 30 Chuyên đề Toán lớp 11: Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số 12;
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay φ = – 60°.
c) Nhận xét về mối liên hệ giữa độ dài các đoạn thẳng AB, A2B2.
Lời giải:
a) Nối O với A và O với B, lấy điểm A1 là trung điểm của đoạn thẳng OA, lấy điểm B1 là trung điểm của đoạn thẳng OB. Khi đó →OA1=12→OA, →OB1=12→OB .
Do đó, A1, B1 tương ứng là ảnh của A, B qua phép vị tự tâm O tỉ số 12 nên đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số 12.
b) Phép quay với góc quay φ = – 60° có chiều quay cùng chiều kim đồng hồ.
Theo chiều quay cùng chiều kim đồng hồ, dựng góc ^A1OA2=60° sao cho OA1 = OA2; dựng góc ^B1OB2=60° sao cho OB1 = OB2. Khi đó ta có A2, B2 tương ứng là ảnh của A1, B1 qua phép quay tâm O với góc quay φ = – 60° nên đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay φ = – 60°.
c) Vì đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số 12 nên A1B1=12AB.
Vì đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay φ = – 60° nên A2B2 = A1B1.
Từ đó suy ra A2B2 = 12AB.
Xem thêm các bài giải Chuyên đề Toán 11 Cánh diều hay, chi tiết khác:
Khởi động trang 26 Chuyên đề Toán lớp 11: Tranh Đông Hồ là một dòng tranh dân gian Việt Nam, xuất xứ từ làng Đông Hồ (xã Song Hồ, huyện Thuận Thành, tỉnh Bắc Ninh). Tranh được in trên giấy điệp, màu sắc được sử dụng là màu tự nhiên: màu đen từ than lá tre, màu xanh từ lá chàm, màu đỏ từ sỏi,... Nghề làm tranh dân gian Đông Hồ là di sản văn hóa phi vật thể cấp Quốc gia.
Hoạt động 1 trang 26 Chuyên đề Toán lớp 11: Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho (Hình 47).
Luyện tập 1 trang 27 Chuyên đề Toán lớp 11: Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số .
Hoạt động 2 trang 27 Chuyên đề Toán lớp 11: Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử A' = V(O, k)(A), B' = V(O, k)(B).
Hoạt động 3 trang 28 Chuyên đề Toán lớp 11: Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử A' = V(O, k)(A), B' = V(O, k)(B), C' = V(O, k)(C).
Luyện tập 2 trang 30 Chuyên đề Toán lớp 11: Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số .
Hoạt động 4 trang 30 Chuyên đề Toán lớp 11: Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:
Luyện tập 3 trang 31 chuyên đề Toán lớp 11: Người ta dùng một kính hiển vi có khả năng phóng to vật lên gấp 100 000 lần để quan sát một virus và đo được kích thước của virus là 2 mm. Hỏi kích thước thật của virus là bao nhiêu micromét (μm)?
Hoạt động 5 trang 31 chuyên đề Toán lớp 11: Quan sát Hình 54 và cho biết:
Luyện tập 4 trang 32 chuyên đề Toán lớp 11: Trong Ví dụ 8, chứng minh rằng hai hình OMGE và COEN đồng dạng với nhau.
Bài 1 trang 32 Chuyên đề Toán 11: Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
Bài 2 trang 32 Chuyên đề Toán 11: Phép biến hình nào trong các phép biến hình dưới đây không là phép đồng dạng?
Bài 3 trang 32 Chuyên đề Toán 11: Khẳng định nào dưới đây là đúng?
Bài 4 trang 32 Chuyên đề Toán 11: Trên bản đồ bay với tỉ lệ xích 1: 10 000 000, khoảng cách giữa Hà Nội và Tokyo đo được là 37,34 cm. Khoảng cách thực tế (tính theo đường chim bay) giữa Hà Nội và Tokyo là bao nhiêu kilômét?
Bài 5 trang 33 Chuyên đề Toán 11: >Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận). Vật sáng AB được đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn OA = 60 cm, qua thấu kính cho ảnh ảo A'B' (Hình 57). A'B' là ảnh của AB qua một phép vị tự tâm O tỉ số k.
Bài 6 trang 33 Chuyên đề Toán 11: Chứng minh rằng qua phép vị tự tâm O tỉ số k (k ≠ 0), ảnh của mọi đường thẳng đi qua tâm O là chính nó.
Bài 7 trang 33 Chuyên đề Toán 11: Cho tam giác nhọn ABC có trực tâm H. Xác định ảnh của tam giác ABC qua phép vị tự tâm H tỉ số k = .
Bài 8 trang 33 Chuyên đề Toán 11: Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Bài 9 trang 33 Chuyên đề Toán 11: Chứng minh rằng nếu phép đồng dạng F biến tam giác ABC thành tam giác A'B'C' thì F biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.
Bài 10 trang 33 Chuyên đề Toán 11: Chứng minh rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau.
Bài 11 trang 33 Chuyên đề Toán 11: Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (Hình 58). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.
Bài 12 trang 33 Chuyên đề Toán 11: Hình 59 mô tả một viên gạch trang trí hình tam giác đều. Chứng minh rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.
