Với giải HĐ2 trang 6 Chuyên đề Toán 11 Kết nối tri thức chi tiết trong Bài 1: Phép biến hình giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm M(x; y) thành điểm M'
HĐ2 trang 6 Chuyên đề Toán 11: Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm M(x; y) thành điểm M'(x + 1; y + 2).
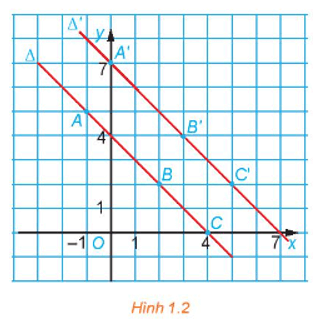
a) Xét các điểm A(– 1; 5), B(2; 2), C(4; 0) thuộc ∆: x + y – 4 = 0. Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu M(x0; y0) là điểm thuộc đường thẳng ∆: x + y – 4 = 0 thì ảnh M'(x0 + 1; y0 + 2) của nó thuộc đường thẳng ∆': x+ y – 7 = 0.
Lời giải:
a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm A'(– 1 + 1; 5 + 2) hay A'(0; 7).
Ảnh của điểm B(2; 3) qua phép biến hình f là điểm B'(2 + 1; 3 + 2) hay B'(3; 5).
Ảnh của điểm C(4; 0) qua phép biến hình f là điểm C'(4 + 1; 0 + 2) hay C'(5; 2).
b) Vì M(x0; y0) thuộc ∆: x + y – 4 = 0 nên x0 + y0 – 4 = 0 hay x0 + y0 = 4
⇔ x0 + y0 + 3 = 4 + 3
⇔ (x0 + 1) + (y0 + 2) = 7
⇔ (x0 + 1) + (y0 + 2) – 7 = 0
Suy ra M'(x0 + 1; y0 + 2) thuộc đường thẳng ∆': x + y – 7 = 0.
Xem thêm các bài giải Chuyên đề Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.