Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G

Ngọc Nguyễn Ngày: 01-07-2023 Lớp 11

345

Với giải Bài 2.11 trang 45 Chuyên đề Toán 11 Kết nối tri thức chi tiết trong Bài 9: Đường đi Euler và đường đi Hamilton giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G

Bài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n - 1}{2}$ ”.

Lời giải:

Cho đơn đồ thị G có 5 đỉnh như hình vẽ sau:

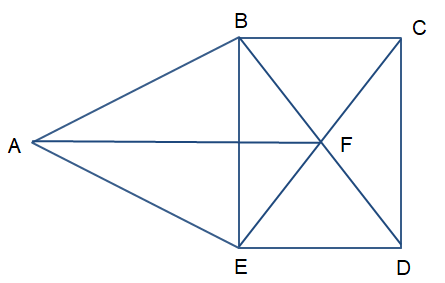
Chuyên đề Toán 11 (Kết nối tri thức) Bài 9: Đường đi Euler và đường đi Hamilton (ảnh 18)

Mỗi đỉnh của đồ thị này đều có bậc là 2 hoặc 3, đều không nhỏ hơn $\frac{5 - 1}{2} = 2$ , thỏa mãn điều kiện của định lí Dirac nếu thay điều kiện “bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ ” bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n - 1}{2}$ ”.

Định lí Dirac là một điều kiện đủ cho sự tồn tại chu trình Hamilton, nhưng đồ thị trên lại không có chu trình Hamilton. Do vậy, đây vì ví dụ cần đưa ra để chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n - 1}{2}$ ”.

Xem thêm các bài giải Chuyên đề Toán 11 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 41 Chuyên đề Toán 11: Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?

HĐ1 trang 41 Chuyên đề Toán 11: Nhận biết đường đi Euler

Luyện tập 1 trang 41 Chuyên đề Toán 11: Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.

HĐ2 trang 43 Chuyên đề Toán 11: Nhận biết đường đi Hamilton

Luyện tập 2 trang 44 Chuyên đề Toán 11: Đồ thị nào trong Hình 2.2.3 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamiton của nó.

Bài 2.7 trang 44 Chuyên đề Toán 11: Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton hay không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.

Bài 2.8 trang 44 Chuyên đề Toán 11: Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?

Bài 2.9 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.

Bài 2.10 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.

Bài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn ”.

Bài 2.12 trang 45 Chuyên đề Toán 11: a) Giả sử G là một đồ thị với n đỉnh và cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.