Toptailieu.vn xin giới thiệu Lý thuyết Các số đặc trưng đo xu thế trung tâm (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Các số đặc trưng đo xu thế trung tâm (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 11
Bài giải Bài 9: Các số đặc trưng đo xu thế trung tâm
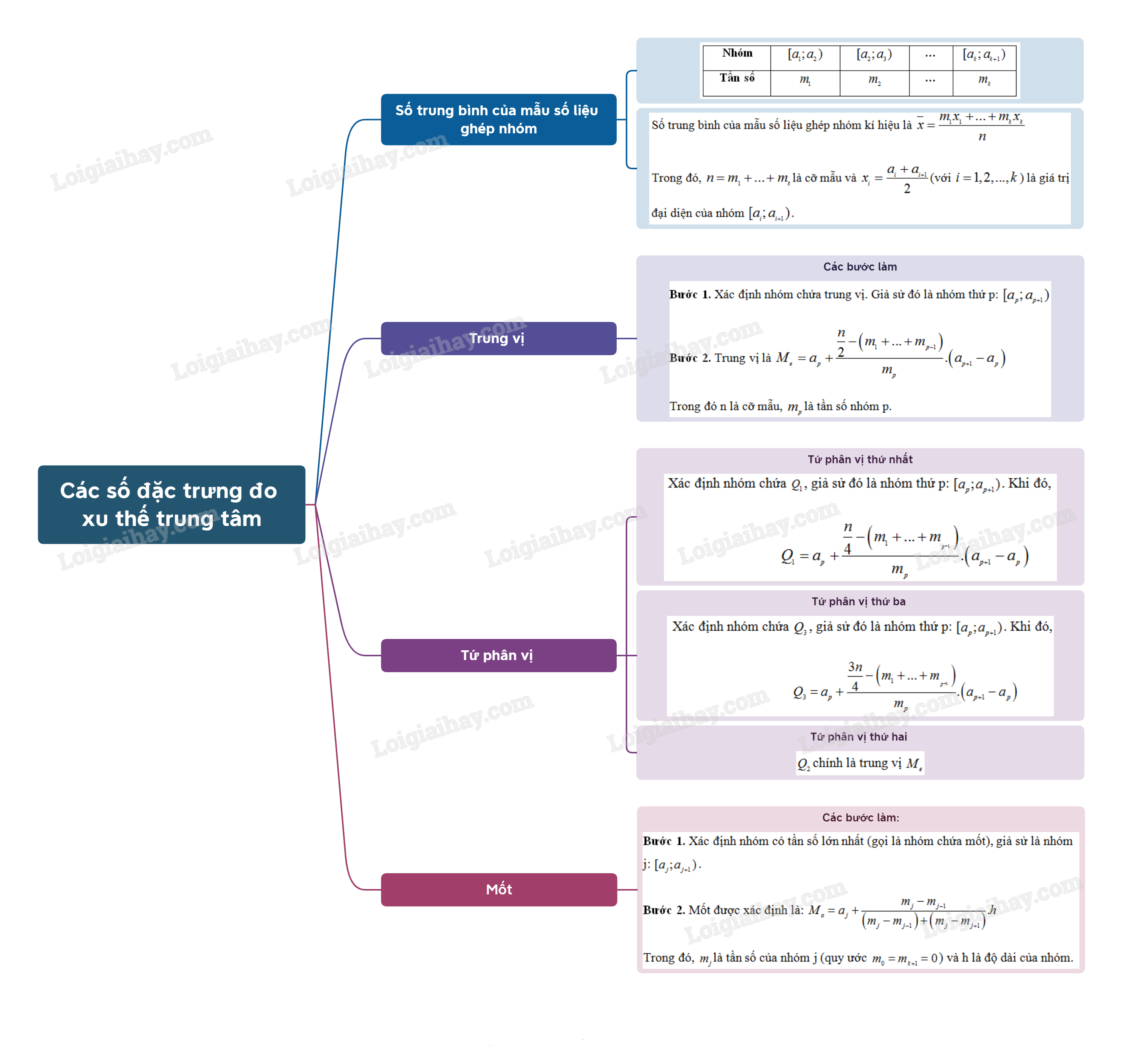
A. Lý thuyết Các số đặc trưng đo xu thế trung tâm
1. Số trung bình của mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là
Trong đó, là cỡ mẫu và (với ) là giá trị đại diện của nhóm .
2. Trung vị của mẫu số liệu ghép nhóm
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: .
Bước 2. Trung vị là
Trong đó n là cỡ mẫu, là tần số nhóm p.
Với , ta quy ước
3. Tứ phân vị của mấu số liệu ghép nhóm
Để tính tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa , giả sử đó là nhóm thứ p: . Khi đó,
Trong đó n là cỡ mẫu, là tần số nhóm p.
Với , ta quy ước
Để tính tứ phân vị thứ ba của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa , giả sử đó là nhóm thứ p: . Khi đó,
Trong đó n là cỡ mẫu, là tần số nhóm p. Với , ta quy ước
Tứ phân vị thứ hai chính là trung vị .
4. Mốt của mẫu số liệu ghép nhóm
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: .
Bước 2. Mốt được xác định là:
Trong đó, là tần số của nhóm j (quy ước ) và h là độ dài của nhóm.
Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.
Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thế trung tâm của mẫu số liệu.
B. Bài tập Các số đặc trưng đo xu thế trung tâm
Bài 1: Kết quả khảo sát cân nặng của 20 quả táo ở mỗi lô hàng A và B được cho bởi bảng sau:
|
Cân nặng (gam) |
[150; 155) |
[155; 160) |
[160; 165) |
[165; 170) |
[170; 175) |
|
Số quả táo lô hàng A |
1 |
4 |
10 |
3 |
2 |
|
Số quả táo lô hàng B |
2 |
3 |
12 |
2 |
1 |
a) Hãy ước lượng cân nặng trung bình của mỗi quả táo ở hai lô hàng trên.
b) Nếu so sánh theo số trung bình thì táo ở lô hàng nào nặng hơn?
Hướng dẫn giải
Trong mỗi khoảng cân nặng, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
|
Cân nặng (gam) |
152,5 |
157,5 |
162,5 |
167,5 |
172,5 |
|
Số quả táo lô hàng A |
1 |
4 |
10 |
3 |
2 |
|
Số quả táo lô hàng B |
2 |
3 |
12 |
2 |
1 |
Tổng số quả táo của mỗi lô hàng A và B đều là n = 20.
Cân nặng trung bình của mỗi quả táo ở lô hàng A là:
(gam)
Cân nặng trung bình của mỗi quả táo ở lô hàng B là:
= 161,75 (gam)
Theo số trung bình thì táo ở lô hàng A nặng hơn táo ở lô hàng B.
Bài 2: Cho mẫu số liệu về cân nặng (kg) của 45 học sinh lớp 11A được cho bởi bảng sau:
|
Cân nặng (kg) |
[40; 45) |
[45; 50) |
[50; 55) |
[55; 60) |
[60; 65) |
|
Số học sinh |
7 |
10 |
20 |
6 |
2 |
Tính tứ phân vị và mốt của mẫu số liệu trên.
Hướng dẫn giải
Cỡ mẫu là n = 7 + 10 + 20 + 6 + 2 = 45
Gọi x1, x2, ….., x45 là cân nặng của 45 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.
Khi đó, trung vị là x23. Do giá trị x23 thuộc nhóm [50; 55) nên nhóm này chứa trung vị.
Do đó p = 3; a3 = 50, m3 = 20; m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5
Khi đó
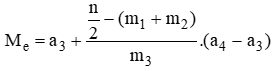
Vậy Me = 51,4.
Từ Me = 51,4, suy ra Q2 = 51,4.
- Tứ phân vị thứ nhất Q1 là trung vị của nửa dãy bên trái Q2 nên .
Do x11 và x12 đều thuộc nhóm [45; 50) nên nhóm này chứa Q1. Do đó, p = 2, a2 = 45, m2 = 10, m1 = 7; a3 – a2 = 5.
Ta có (a3-a2) .
- Tứ phân vị thứ ba Q3 là trung vị của nửa dãy bên phải Q2 nên .
Do x34 và x35 đều thuộc nhóm [50; 55) nên nhóm này chứa Q3. Do đó, p = 3, a3 = 50, m3 = 20, m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5.
Ta có 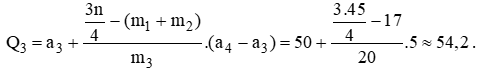
Vậy tứ phân vị: Q1 ≈ 47,1; Q2 ≈ 51,4; Q3 ≈ 54,2.
- Ta thấy tần số lớn nhất là 20 nên nhóm chứa mốt là nhóm [50; 55).
Ta có j = 3, a3 = 50, m3 = 20, m2 = 10, m4 = 6, h = 55 – 50 = 5
Khi đó
Vậy Mo ≈ 52,1.
Xem thêm Lý thuyết các bài Toán 11 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 8: Mẫu số liệu ghép nhóm
Lý thuyết Bài 10: Đường thẳng và mặt phẳng trong không gian
Lý thuyết Bài 11: Hai đường thẳng song song
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.