Khởi động trang 49 Chuyên đề Toán 11: Thành phố Königsberg thuộc Phổ (nay là Kaliningrad thuộc Nga) có bảy cây cầu nối bốn vùng đất được chia bởi các nhánh sông Pregel như hình dưới.

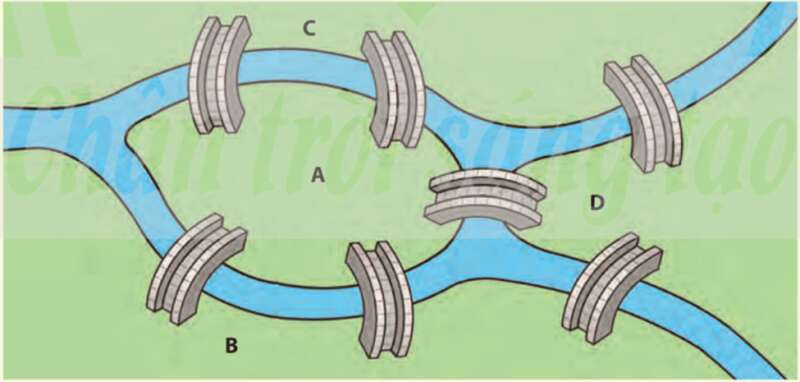
Vào mỗi sáng Chủ nhật, người dân thành phố thường đi dạo qua các cây cầu. Họ tự hỏi không biết có thể bắt đầu từ một điểm nào đó trong thành phố, đi qua khắp các cây cầu, mỗi cầu chỉ đi qua một lần, rồi quay về điểm xuất phát.

Theo em, có hay không một cách đi như vậy?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được bài toán trên như sau:

Biểu thị mỗi vùng đất bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.

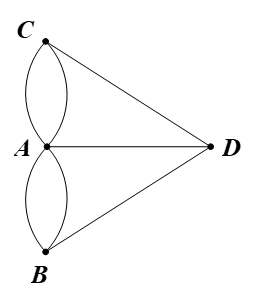
Ta thấy d(A) = 5; d(B) = d(C) = d(D) = 3.

Suy ra tất cả các đỉnh của đồ thị trên đều có bậc lẻ.

Do đó đồ thị không có chu trình Euler.

Nói cách khác, không thể bắt đầu từ một điểm nào đó trong thành phố, đi qua khắp các cây cầu, mỗi cầu chỉ đi qua một lần, rồi quay về điểm xuất phát.

1. Đường đi Euler

Khám phá 1 trang 50 Chuyên đề Toán 11: a) Nếu coi mỗi vùng đất của thành phố Königsberg là một đỉnh, mỗi cây cầu là một cạnh nối hai đỉnh thì ta được một đồ thị G như Hình 1.

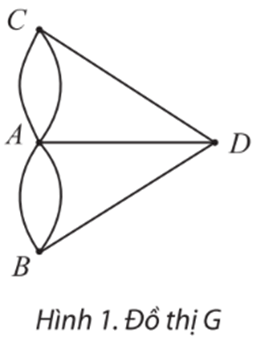
Câu hỏi của người dân thành phố trở thành: có hay không cách vẽ bằng một nét bút liền (không nhấc bút) đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, sao cho điểm kết thúc trùng với điểm xuất phát?

Hãy thử vẽ và đưa ra dự đoán của mình.

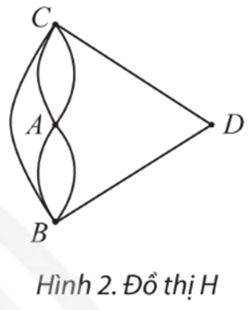
b) Nếu không có cây cầu nối giữa A và D nhưng có thêm một cây cầu nối B và C thì ta có đồ thị H như Hình 2. Có thể vẽ một nét liền đi qua tất cả các cạnh của đồ thị này, mỗi cạnh đúng một lần không?

Lời giải:

a) Sau khi thử vẽ, ta dự đoán: không có cách vẽ bằng một nét bút liền (không nhấc bút) đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, sao cho điểm kết thúc trùng với điểm xuất phát.

b) Ta có thể vẽ một nét liền đi qua tất cả các cạnh của đồ thị này, mỗi cạnh đúng một lần bằng cách lần lượt vẽ các cạnh m, s, r, n, CB, BD, DC.

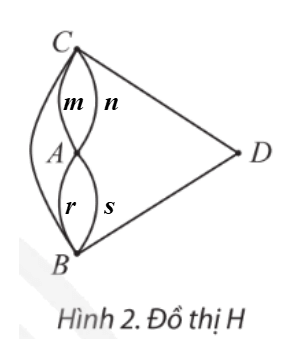
Chú ý: Ta có thể bắt đầu vẽ từ đỉnh khác và có thể thay đổi thứ tự các cạnh (đường cong) trong khi vẽ miễn là cách vẽ đó thỏa mãn yêu cầu bài toán.

Khám phá 2 trang 51 Chuyên đề Toán 11: a) Chỉ ra một chu trình Euler của đồ thị G ở Hình 5. Đồ thị này có đỉnh nào bậc lẻ không?

b) Chỉ ra rằng các đồ thị S và T sau đây không có chu trình Euler. Các đồ thị này có đỉnh bậc lẻ không?

Lời giải:

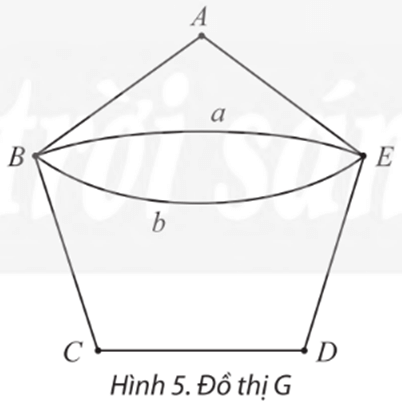
a) Một chu trình Euler của đồ thị G là: AB, a, b, BC, CD, DE, EA.

Ta có d(A) = 2; d(B) = 4; d(C) = 2; d(D) = 2; d(E) = 4.

Vậy đồ thị đã cho không có đỉnh nào là đỉnh bậc lẻ.

b) Đồ thị S không có chu trình Euler vì nếu một đường đi bắt đầu và kết thúc tại cùng một đỉnh thì cạnh CD bắt buộc phải đi qua ít nhất hai lần; nếu một đường đi bắt đầu tại đỉnh này và kết thúc tại đỉnh kia thì không được gọi là chu trình.

Tương tự như vậy, đồ thị T không có chu trình Euler.

Đồ thị S có: d(A) = 2; d(B) = 2; d(C) = 3; d(D) = 1.Suy ra đồ thị S có hai đỉnh bậc lẻ là C, D.

Đồ thị T có: d(A) = 3; d(B) = 2; d(C) = 3; d(D) = 2.Suy ra đồ thị T có hai đỉnh bậc lẻ là A, C.

Vậy cả hai đồ thị S và T đều có đỉnh bậc lẻ.

Khám phá 3 trang 52 Chuyên đề Toán 11: Hãy chỉ ra một đường đi Euler trên mỗi đồ thị sau. Mỗi đồ thị có bao nhiêu đỉnh bậc lẻ?

Lời giải:

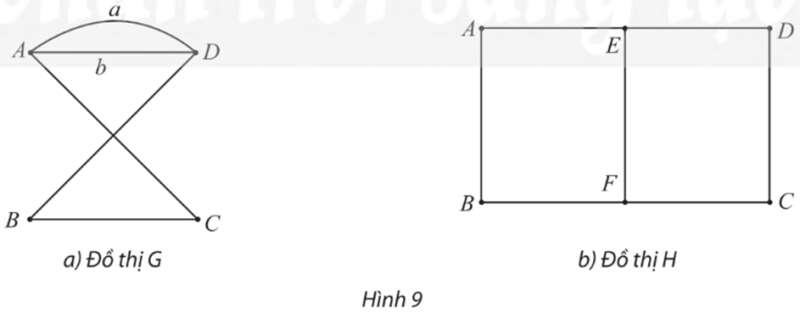
Một đường đi Euler (từ A đến D) trên đồ thị G là: ACBDAD.

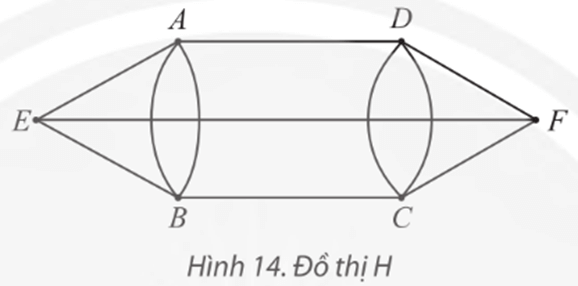
Một đường đi Euler (từ E đến F) trên đồ thị H là: EABFCDEF.

Đồ thị G có: d(A) = 3; d(B) = 2; d(C) = 2; d(D) = 3.Suy ra đồ thị G có hai đỉnh bậc lẻ là A, D.

Đồ thị H có: d(A) = 2; d(B) = 2; d(C) = 2; d(D) = 2; d(E) = 3; d(F) = 3.Suy ra đồ thị H có hai đỉnh bậc lẻ là E, F.

Vậy đồ thị G có 2 đỉnh bậc lẻ, đồ thị H có 2 đỉnh bậc lẻ.

Thực hành 1 trang 54 Chuyên đề Toán 11: Mỗi đồ thị sau đây có chu trình Euler không? Nếu có, hãy chỉ ra một chu trình như vậy.

Thực hành 2 trang 54 Chuyên đề Toán 11: Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.

Lời giải:

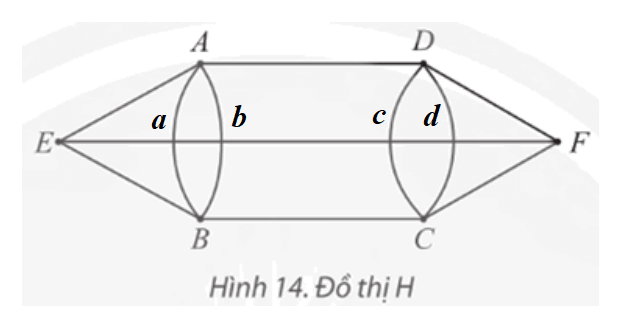
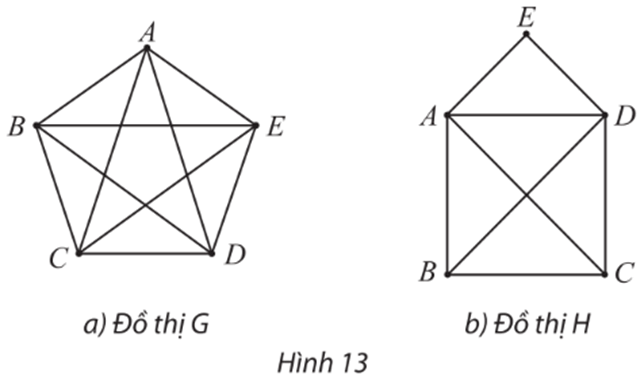
Ta có d(A) = d(B) = d(C) = d(D) = 4 và d(E) = d(F) = 3.

Suy ra đồ thị H có đúng 2 đỉnh bậc lẻ là E, F.

Do đó đồ thị H có đường đi Euler.

Chẳng hạn, bắt đầu từ đỉnh E, ta có thể đi theo đường đi Euler: EAabADcdDFCBEF.

Lời giải:

a) Đồ thị G:

Ta có d(A) = d(B) = d(C) = d(D) = d(E) = 4.

Vậy đồ thị G có chu trình Euler vì các đỉnh của đồ thị G đều có bậc chẵn.

Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo chu trình Euler: ABECAEDCBDA.

b) Đồ thị H:

Ta có d(A) = d(D) = 4; d(B) = d(C) = 3; d(E) = 2.

Vậy đồ thị H không có chu trình Euler vì hai đỉnh B, C có bậc lẻ.

Vận dụng 1 trang 54 Chuyên đề Toán 11: Hãy giải đáp câu hỏi của người dân Königsberg ở Hoạt động khởi động (còn gọi là bài toán Bảy cây cầu).

Lời giải:

Biểu thị mỗi vùng đất bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.

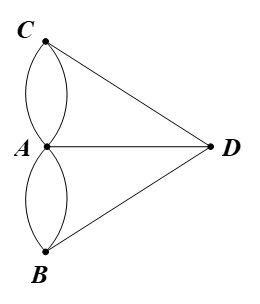
Ta thấy d(A) = 5; d(B) = d(C) = d(D) = 3.

Suy ra tất cả các đỉnh của đồ thị trên đều có bậc lẻ.

Do đó đồ thị không có chu trình Euler.

Nói cách khác, không thể bắt đầu từ một điểm nào đó trong thành phố, đi qua khắp các cây cầu, mỗi cầu chỉ đi qua một lần, rồi quay về điểm xuất phát.

2. Đường đi Hamilton

Khám phá 4 trang 54 Chuyên đề Toán 11: Đồ thị ở Hình 15b biểu diễn các điểm vui chơi trong một công viên với những con đường nối giữa chúng như Hình 15a. Có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần hay không? Nếu có, chỉ ra ít nhất một đường đi như vậy.

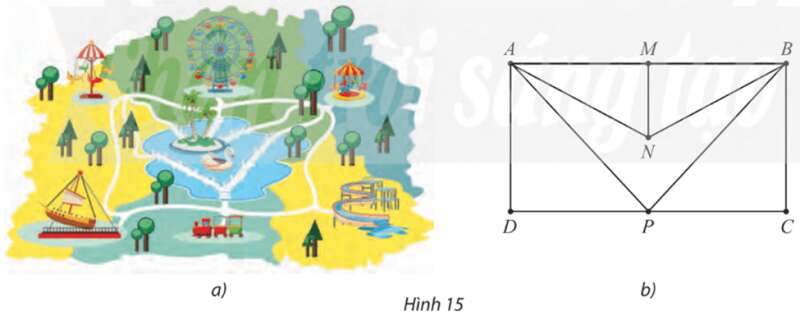
Lời giải:

Ta có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần.

Chẳng hạn, ta có thể đi theo một số đường đi như sau: ANMBCPD, NBMADPC, DANMBCP,…

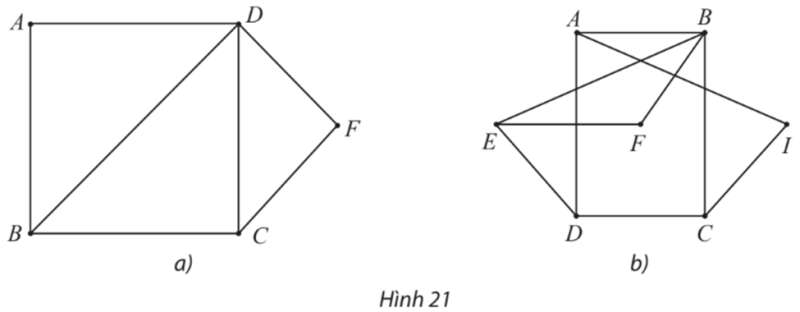
Thực hành 3 trang 57 Chuyên đề Toán 11: Hãy chỉ ra rằng mỗi đồ thị sau đây có chu trình Hamilton.

Lời giải:

⦁ Hình 21a:

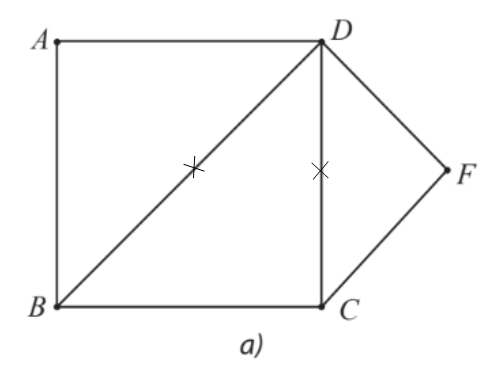
Đồ thị ở Hình 21a có các đỉnh A, F có bậc 2.

Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, FD, FC trong đồ thị ở Hình 21a.

Do đó h không thể đi qua các cạnh BD, DC.

Nếu xóa đi hai cạnh này thì đỉnh B, C trở thành có bậc 2.

Vì vậy h phải đi qua cạnh BC.

Khi đó ta được chu trình Hamilton h: ADFCBA.

⦁ Hình 21b:

Đồ thị ở Hình 21b có các đỉnh F, I có bậc 2.

Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh FE, FB, IA, IC.

Do đó ta được chu trình Hamilton h: AICBFEDA (hoặc AICDEFBA).

Vậy cả hai đồ thị đã cho đều có chu trình Hamilton.

Vận dụng 2 trang 58 Chuyên đề Toán 11: Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố, các cạnh biểu thị đường đi giữa các điểm du lịch này. Có hay không một cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch?

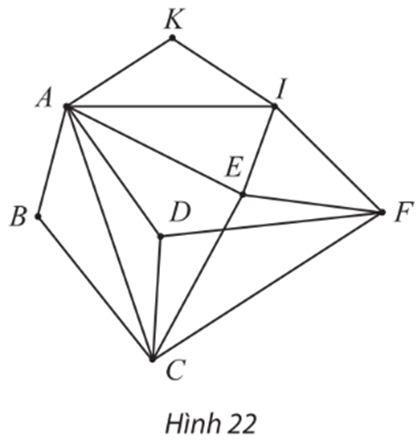
Lời giải:

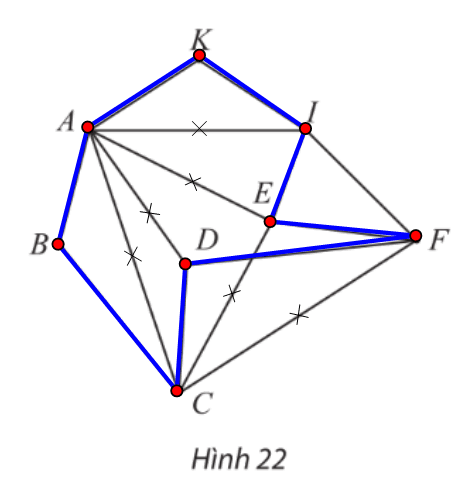
Đồ thị ở Hình 22 có các đỉnh B, K có bậc 2.

Suy ra chu trình Hamilton h (nếu có) phải đi các các cạnh AB, BC, AK, KI.

Do đó h không thể đi qua các cạnh AI, AD, AD, AE.

Nếu xóa đi bốn cạnh trên thì các đỉnh A, D trở thành bậc 2.

Suy ra h phải đi qua các cạnh AB, AK, DC, DF.

Do đó h không thể đi qua các cạnh CE, CF.

Nếu xóa đi thêm hai cạnh trên thì đỉnh E trở thành bậc 2.

Suy ra h phải đi qua các cạnh EI, EF.

Vì vậy ta được chu trình Hamilton h: ABCDFEIKA.

Vậy có cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch.

Bài tập

Bài 1 trang 58 Chuyên đề Toán 11: Mỗi đồ thị trong Hình 23 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy.

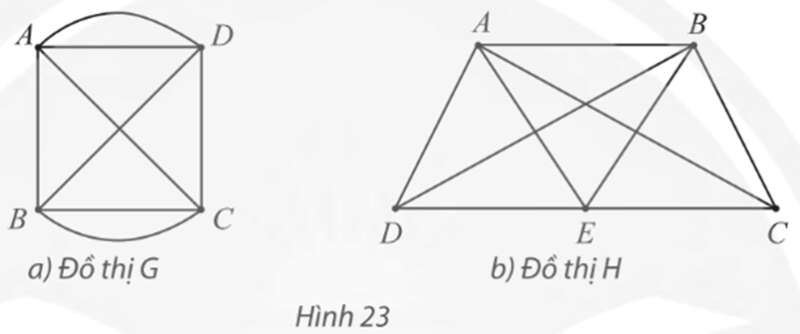
Lời giải:

⦁ Đồ thị G:

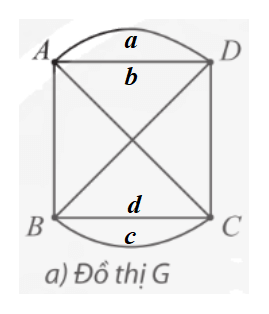
Ta có d(A) = d(B) = d(C) = d(D) = 4.

Suy ra đồ thị G có tất cả các đỉnh đều có bậc chẵn.

Vậy đồ thị G có chu trình Euler.

Chẳng hạn, ta có chu trình Euler: AabACDBcdBA.

⦁ Đồ thị H:

Ta có d(A) = d(B) = d(E) = 4; d(C) = d(D) = 3.

Suy ra đồ thị H có hai đỉnh C, D có bậc lẻ.

Vậy đồ thị H không có chu trình Euler.

Bài 2 trang 58 Chuyên đề Toán 11: Đồ thị ở Hình 24 có đường đi Euler không? Nếu có hãy chỉ ra một đường đi như vậy.

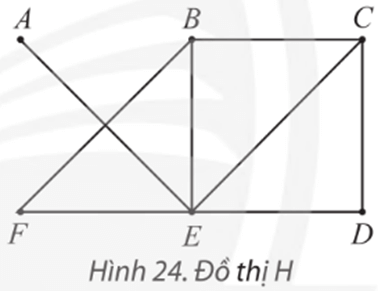
Lời giải:

Ta có d(A) = 1; d(B) = d(C) = 3; d(D) = d(F) = 2; d(E) = 5.

Đồ thị H có 3 đỉnh có bậc lẻ nên không có đường đi Euler.

Bài 3 trang 58 Chuyên đề Toán 11: Chỉ ra một chu trình Hamilton của đồ thị ở Hình 25.

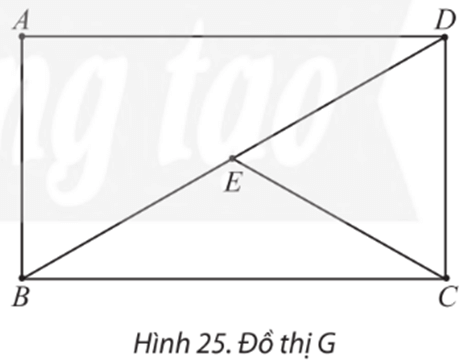
Lời giải:

Một số chu trình Hamilton của đồ thị G là: BADECB, BECDAB, ADECBA,…

Chú ý: Đồ thị G có thể có các chu trình Hamilton khác bắt đầu từ một trong các đỉnh còn lại.

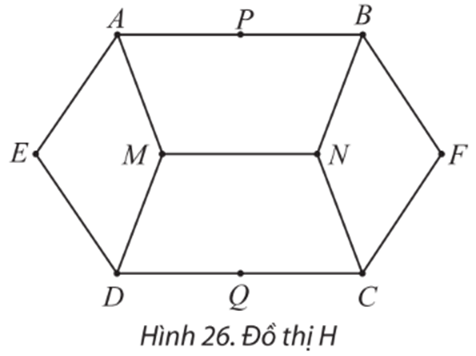
Bài 4 trang 58 Chuyên đề Toán 11: Chỉ ra một đường đi Hamilton của đồ thị ở Hình 26.

Lời giải:

Một số đường đi Hamilton của đồ thị H là: EDQCFBNMAP, EAPBNMDQCF, FBPAEDMNCQ,…

Chú ý: Đồ thị H có thể có các đường đi Hamilton khác.

Bài 5 trang 59 Chuyên đề Toán 11: Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27. Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát? Nếu có, hãy chỉ ra một cách đi như vậy.

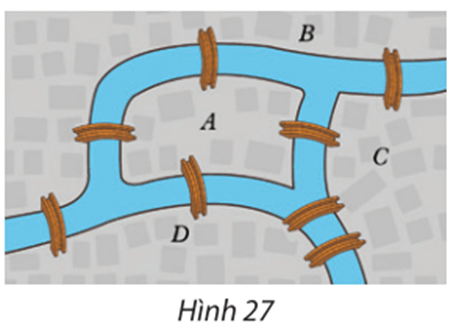
Lời giải:

Biểu thị mỗi khu phố bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.

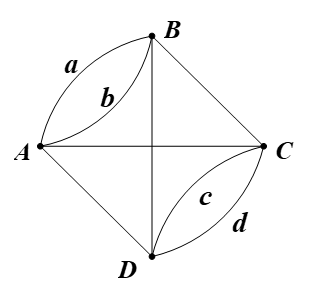
Ta có d(A) = d(B) = d(C) = d(D) = 4.

Suy ra tất cả các đỉnh của đồ thị trên đều có bậc chẵn.

Do đó đồ thị trên có chu trình Euler.

Vậy nói cách khác, có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát.

Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo chu trình Euler: AabADcdDBCA.

Bài 6 trang 59 Chuyên đề Toán 11: Có năm vùng đất A, B, C, D và E được nối với nhau bằng những cây cầu như Hình 28.

a) Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát?

b) Nếu không yêu cầu quay lại nơi bắt đầu thì có cách đi như vậy không? Nếu có, hãy chỉ ra một cách đi.

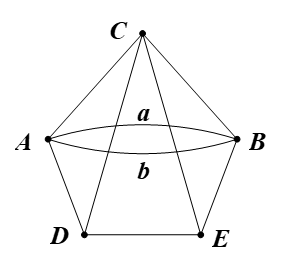
Lời giải:

a) Biểu thị mỗi vùng đất bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.

Ta có d(A) = d(B) = d(C) = 4; d(D) = d(E) = 3.

Suy ra đồ thị trên có đúng hai đỉnh bậc lẻ là D, E.

Do đó đồ thị trên có đường đi Euler nhưng không có chu trình Euler.

Vậy nói cách khác, không có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát.

b) Nếu không yêu cầu quay lại nơi bắt đầu thì có cách đi như vậy (vì đồ thị trên có đường đi Euler).

Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo đường đi Euler: DACDECBabBE.