Với giải Bài 5 trang 59 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài 2: Đường đi Euler và đường đi Hamilton giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
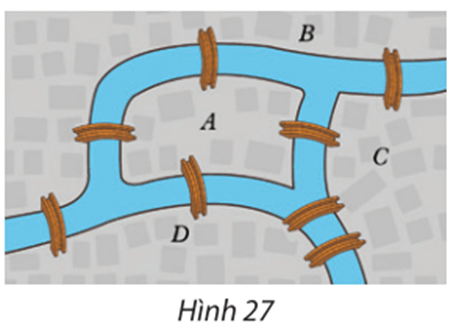
Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27
Bài 5 trang 59 Chuyên đề Toán 11: Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27. Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát? Nếu có, hãy chỉ ra một cách đi như vậy.
Lời giải:
Biểu thị mỗi khu phố bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.
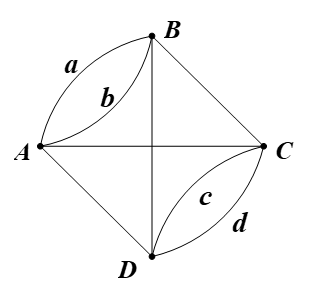
Ta có d(A) = d(B) = d(C) = d(D) = 4.
Suy ra tất cả các đỉnh của đồ thị trên đều có bậc chẵn.
Do đó đồ thị trên có chu trình Euler.
Vậy nói cách khác, có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát.
Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo chu trình Euler: AabADcdDBCA.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 3 trang 57 Chuyên đề Toán 11: Hãy chỉ ra rằng mỗi đồ thị sau đây có chu trình Hamilton.
Bài 3 trang 58 Chuyên đề Toán 11: Chỉ ra một chu trình Hamilton của đồ thị ở Hình 25.
Bài 4 trang 58 Chuyên đề Toán 11: Chỉ ra một đường đi Hamilton của đồ thị ở Hình 26.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.