Với giải Vận dụng 2 trang 58 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài 2: Đường đi Euler và đường đi Hamilton giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố
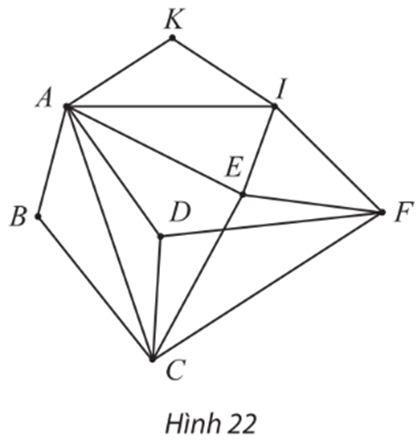
Vận dụng 2 trang 58 Chuyên đề Toán 11: Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố, các cạnh biểu thị đường đi giữa các điểm du lịch này. Có hay không một cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch?
Lời giải:
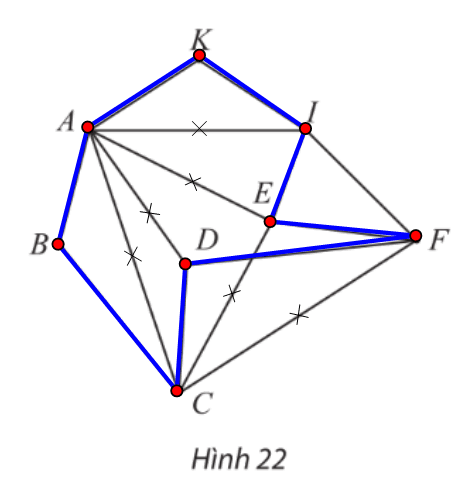
Đồ thị ở Hình 22 có các đỉnh B, K có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi các các cạnh AB, BC, AK, KI.
Do đó h không thể đi qua các cạnh AI, AD, AD, AE.
Nếu xóa đi bốn cạnh trên thì các đỉnh A, D trở thành bậc 2.
Suy ra h phải đi qua các cạnh AB, AK, DC, DF.
Do đó h không thể đi qua các cạnh CE, CF.
Nếu xóa đi thêm hai cạnh trên thì đỉnh E trở thành bậc 2.
Suy ra h phải đi qua các cạnh EI, EF.
Vì vậy ta được chu trình Hamilton h: ABCDFEIKA.
Vậy có cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 49 Chuyên đề Toán 11: Thành phố Königsberg thuộc Phổ (nay là Kaliningrad thuộc Nga) có bảy cây cầu nối bốn vùng đất được chia bởi các nhánh sông Pregel như hình dưới.
Khám phá 1 trang 50 Chuyên đề Toán 11: a) Nếu coi mỗi vùng đất của thành phố Königsberg là một đỉnh, mỗi cây cầu là một cạnh nối hai đỉnh thì ta được một đồ thị G như Hình 1.
Khám phá 2 trang 51 Chuyên đề Toán 11: a) Chỉ ra một chu trình Euler của đồ thị G ở Hình 5. Đồ thị này có đỉnh nào bậc lẻ không?
Khám phá 3 trang 52 Chuyên đề Toán 11: Hãy chỉ ra một đường đi Euler trên mỗi đồ thị sau. Mỗi đồ thị có bao nhiêu đỉnh bậc lẻ?
Thực hành 1 trang 54 Chuyên đề Toán 11: Mỗi đồ thị sau đây có chu trình Euler không? Nếu có, hãy chỉ ra một chu trình như vậy.
Thực hành 2 trang 54 Chuyên đề Toán 11: Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.
Vận dụng 1 trang 54 Chuyên đề Toán 11: Hãy giải đáp câu hỏi của người dân Königsberg ở Hoạt động khởi động (còn gọi là bài toán Bảy cây cầu).
Khám phá 4 trang 54 Chuyên đề Toán 11: Đồ thị ở Hình 15b biểu diễn các điểm vui chơi trong một công viên với những con đường nối giữa chúng như Hình 15a. Có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần hay không? Nếu có, chỉ ra ít nhất một đường đi như vậy.
Thực hành 3 trang 57 Chuyên đề Toán 11: Hãy chỉ ra rằng mỗi đồ thị sau đây có chu trình Hamilton.
Vận dụng 2 trang 58 Chuyên đề Toán 11: Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố, các cạnh biểu thị đường đi giữa các điểm du lịch này. Có hay không một cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch?
Bài 1 trang 58 Chuyên đề Toán 11: Mỗi đồ thị trong Hình 23 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy.
Bài 2 trang 58 Chuyên đề Toán 11: Đồ thị ở Hình 24 có đường đi Euler không? Nếu có hãy chỉ ra một đường đi như vậy.
Bài 3 trang 58 Chuyên đề Toán 11: Chỉ ra một chu trình Hamilton của đồ thị ở Hình 25.
Bài 4 trang 58 Chuyên đề Toán 11: Chỉ ra một đường đi Hamilton của đồ thị ở Hình 26.
Bài 5 trang 59 Chuyên đề Toán 11: Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27. Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát? Nếu có, hãy chỉ ra một cách đi như vậy.
Bài 6 trang 59 Chuyên đề Toán 11: Có năm vùng đất A, B, C, D và E được nối với nhau bằng những cây cầu như Hình 28.

