Toptailieu biên soạn và giới thiệu Phương pháp giải bài tập Cách nhân đơn thức với đa thức, nhân đa thức với đa thức (MỚI NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 8 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải bài tập Cách nhân đơn thức với đa thức, nhân đa thức với đa thức (MỚI NHẤT 2024)

A. Cách nhân đơn thức với đa thức

I. Quy tắc:

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức rồi cộng các tích của chúng lại với nhau.

Với mọi $x,y\ne 0;m,$$n\in \mathbb{N},m\ge n$ thì:

$\begin{array}{l}{x}^m.x^n=x^{m+n}\\ x^m.y^m={\left(xy\right)}^m\end{array}$

II. Các dạng bài

Dạng 1: Rút gọn biểu thức sử dụng phép nhân đa thức với đơn thức

1. Phương pháp giải:

- Sử dụng quy tắc nhân đa thức với đơn thức để phá ngoặc và kết hợp với các phép toán liên quan đến lũy thừa để rút gọn biểu thức

2. Ví dụ minh họa

VD1: Làm tính nhân:

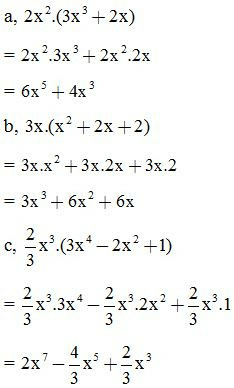
VD2: Rút gọn biểu thức:  

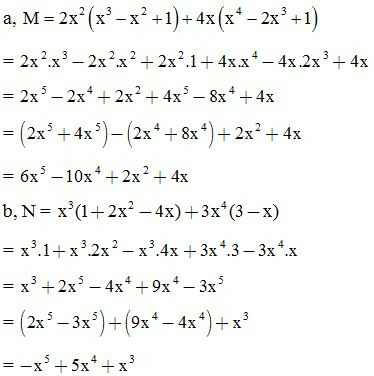
Dạng 2: Tính giá trị biểu thức cho trước

1. Phương pháp giải:

Sử dụng quy tắc nhân đa thức với đơn thức để rút gọn biểu thức đã cho sau đó thay các giá trị của biến vào biểu thức đã rút gọn.

2. Ví dụ minh họa

VD1: Thực hiện phép tính rồi tính giá trị biểu thức:

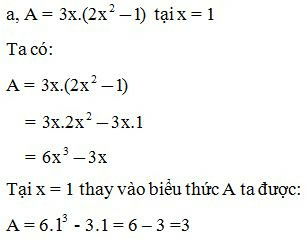
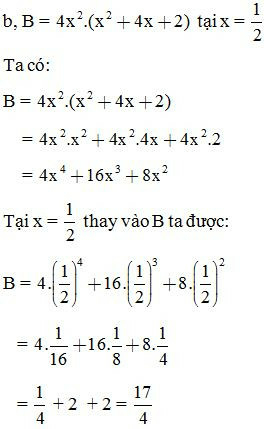
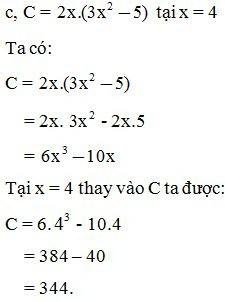
Dạng 3: Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến

1. Phương pháp giải:

Sử dụng quy tắc nhân đa thức với đơn thức để rút gọn biểu thức và kết quả thu được sau khi rút gọn không còn chứa biến

2. Ví dụ minh họa:

Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x, biết:

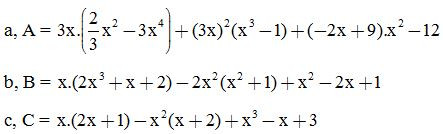
Lời giải:

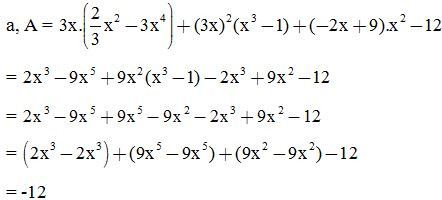
Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của biến x

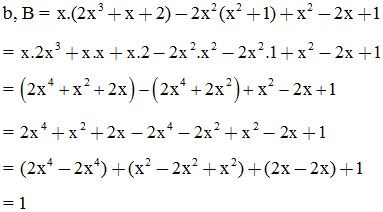
Vậy giá trị của biểu thức B không phụ thuộc vào giá trị của biến x

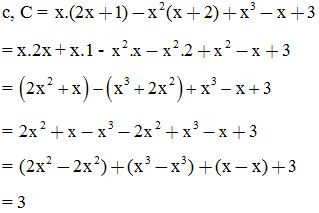
Vậy giá trị của biểu thức C không phụ thuộc vào giá trị của biến x

Dạng 4: Tìm x thỏa mãn điều kiện cho trước:

a. Phương pháp giải:

- B1: Sử dụng quy tắc nhân đơn thức với đa thức để phá ngoặc

- B2: Nhóm các đơn thức đồng dạng với nhau lại và rút gọn biểu thức ở hai vế để tìm x.

b. Ví dụ minh họa:

Tìm x, biết:

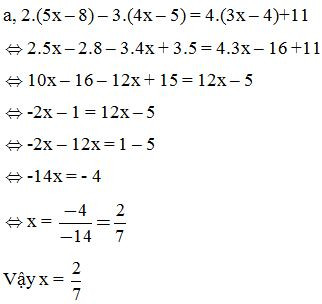
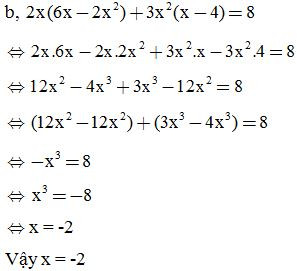
B. Cách nhân đa thức với đa thức:

I. Quy tắc:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng tích với nhau

Ta có:

(A + B).(C + D)

= A.(C + D) + B.(C + D)

= A.C + A.D + B.C + B.D

II. Các dạng bài:

Dạng 1: Rút gọn biểu thức

1. Phương pháp giải:

Sử dung quy tắc nhân đa thức với đa thức.

2. Ví dụ minh họa:

VD1: Thực hiện phép tính:

Dạng 2: Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến

1. Phương pháp giải:

Sử dụng quy tắc nhân đa thức với đa thức để rút gọn biểu thức và kết quả thu được sau khi rút gọn không còn chứa biến.

2. Ví dụ minh họa:

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x, biết:

a, P = (x + 2).(x – 3) – x(x – 6) + 7

Ta có:

P = (x + 2).(x – 3) – x(x – 1) + 7

= x(x – 3) + 2.(x – 3) -$x^2$ + x + 7

= $x^2$ - 3x + 2x – 6 - $x^2$+ x + 7

= $x^2$ - x – 6 - $x^2$+ x + 7

= ($x^2-x^2$) + (x – x) + (7 – 6)

= 1

Vậy giá trị của biểu thức P không phụ thuộc vào giá trị của biến x

b, Q = (x + 2).(3x – 1) – x(3x + 3) – 2x + 7

Ta có:

Q = (x + 2).(3x – 1) – x(3x + 3) – 2x + 7

= x.(3x – 1) + 2.(3x – 1) – x.(3x + 3) – 2x + 7

= $3x^2$ - x + 6x – 2 - $3x^2$ - 3x – 2x + 7

= ($3x^2-3x^2$) + (6x – x – 3x – 2x) + (7 – 2)

= 5

Vậy giá trị của biểu thức Q không phụ thuộc vào giá trị của biến x

c, T = (2x – 3)(2x + 3) – x(3 + 4x) + 3x + 1

Ta có:

T =  (2x – 3)(2x + 3) – x(3 + 4x) + 3x + 1

= 2x.(2x + 3) – 3.(2x + 3) – x(3 + 4x) + 3x + 1

= $4x^2$ + 6x – 6x – 9 – 3x - $4x^2$ + 3x + 1

= ($4x^2-4x^2$) + (6x – 6x – 3x + 3x) + (1 – 9)

= -8

Vậy giá trị của biểu thức T không phụ thuộc vào giá trị của biến x

Dạng 3: Tìm x thỏa mãn điều kiện cho trước

a. Phương pháp giải:

- B1: Sử dụng quy tắc nhân đa thức với đa thức để phá ngoặc

- B2: Nhóm các đơn thức đồng dạng với nhau lại và rút gọn biểu thức ở hai vế để tìm x.

b. Ví dụ minh họa:

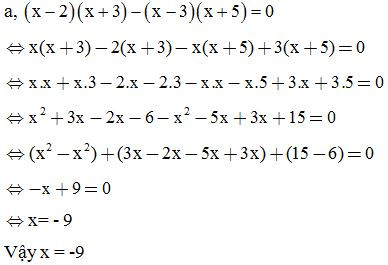
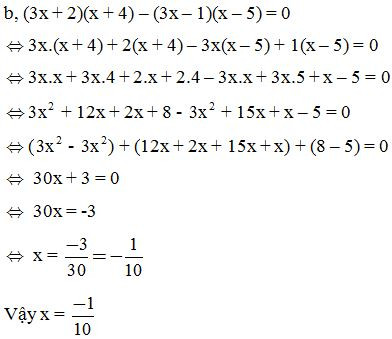
Dạng 4: Chứng minh đẳng thức bằng nhau

a. Phương pháp giải:

Ta chọn một trong hai vế của biểu thức để thực hiện phép nhân đa thức với đa thức, sau đó rút gọn đa thức tích để thu được kết quả như vế còn lại.

b. Ví dụ minh họa:

Chứng minh

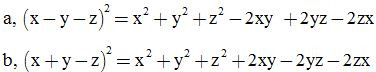
Giải:

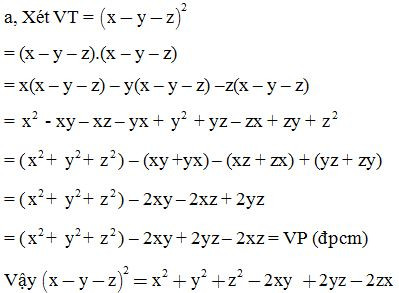
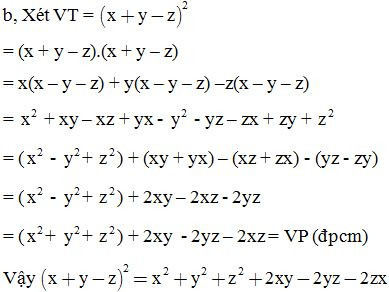
C. Bài tập vận dụng

Bài 1: Thực hiện phép tính:

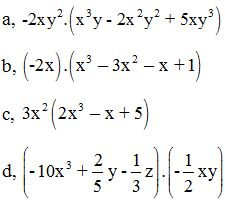
ĐS:

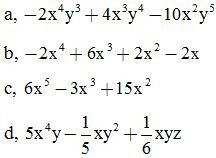
Bài 2: Thực hiện phép tính:

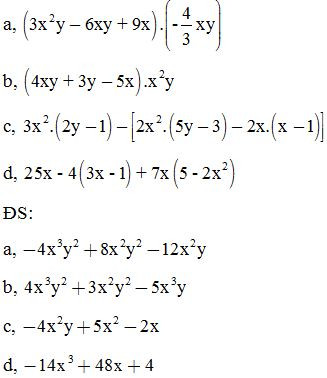
Bài 3: Thực hiện phép tính rồi tính giá trị của các biểu thức sau, biết:            

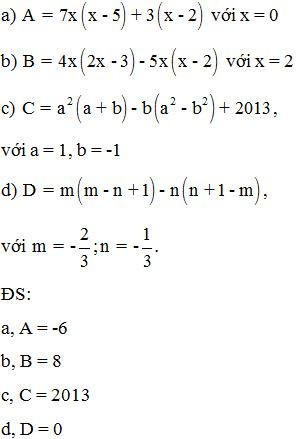
Bài 4: Chứng minh rằng các biểu thức sau không phụ thuộc vào giá trị của biến x, biết:

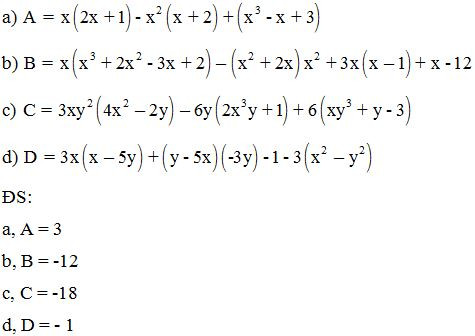
Bài 5: Tìm x, biết:

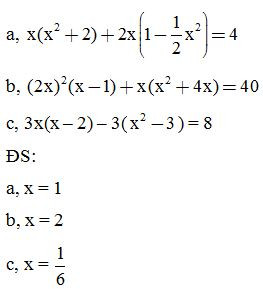
Bài 6: Thực hiện phép tính:

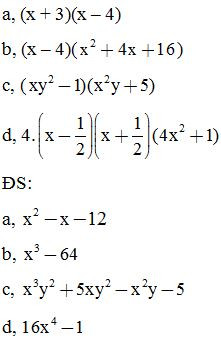
Bài 7: Rút gọn rồi tính giá trị của các biểu thức sau:

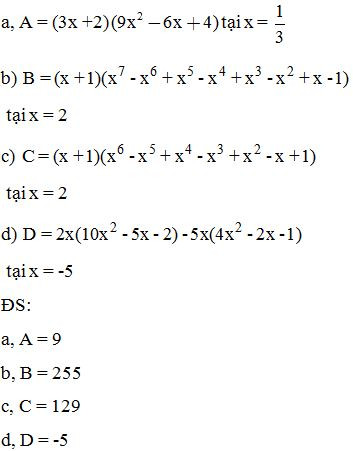
Bài 8: Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x:

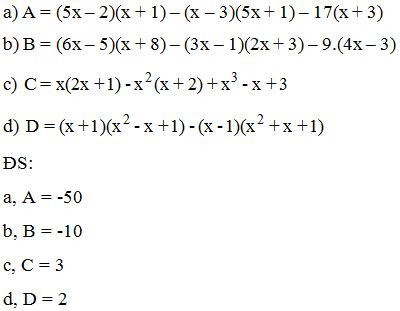
Bài 9: Tìm x, biết:

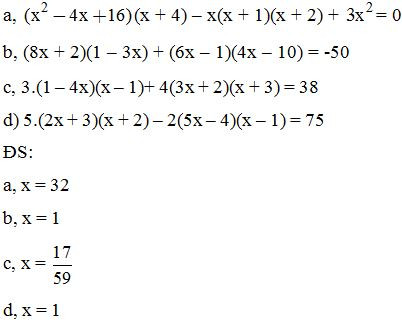
Bài 10: Chứng minh:

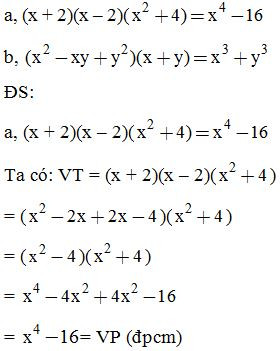
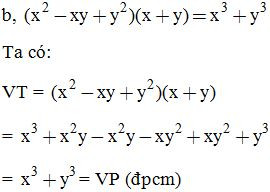
Bài 11: Tìm ba số tự nhiên liên tiếp, biết tích của hai số sau lớn hơn tích của hai số đầu là 52.

ĐS:

Gọi ba số tự nhiên liên tiếp lần lượt là: x, x + 1, x + 2 (x$\in N$).

Ta có tích của hai số đầu là x.(x + 1)

Tích của hai số sau là: (x + 1)(x + 2)

Vì tích của hai số sau lớn hơn tích của hai số đầu là 52 nên ta có:

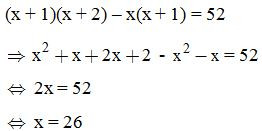
Vậy ba số tự nhiên liên tiếp là: 26, 27, 28.

Bài 12: Cho a và b là hai số tự nhiên. Biết a chia cho 5 dư 1, b chia cho 5 dư 4. Chứng minh ab + 1 chia hết cho 5

ĐS:

Ta có a chia cho 5 dư 1 nên ta đặt a = 5x + 1 (x$\in N$)

Ta lại có b chia cho 5 dư 4 nên ta đặt b = 5y + 4 (y$\in N$)

Ta có:

ab + 1 = (5x +1)(5y + 4) + 1

= 25xy + 20x + 5y + 4 + 1

= 25xy + 20x + 5y + 5

= 5.(5xy +4x + y + 1)$⋮$5 (đpcm)

Bài 13: Chứng minh 2n²(n + 1) - 2n(n² + n - 3) chia hết cho 6 với mọi số nguyên n.

ĐS:

Ta có:

2n²(n + 1) - 2n(n² + n - 3)

= 2n³ + 2n² - 2n³ - 2n² +6n

= 6n$⋮$6 (đpcm)

Bài 14: Chứng minh n(3 – 2n) – (n – 1)(1 + 4n) – 1 chia hết cho 6 với mọi số nguyên n

ĐS: chứng minh tương tự bài 13

D. Bài tập tự luyện

Bài 1: Giá trị của biểu thức A = x( 2x + 3 ) - 4( x + 1 ) - 2x( x - 1/2 ) là ?

A. x +1   

B. 4

C. - 4   

D. 1 -x

Lời giải:

Ta có: A = x( 2x + 3 ) - 4( x + 1 ) - 2x( x - 1/2 )

= ( 2x .x + 3 .x ) - ( 4 .x + 4 .1 ) - ( 2x .x - 1/2 .2x )

= 2x² + 3x - 4x - 4 - 2x² + x = - 4

Chọn đáp án C.

Bài 2: Chọn câu trả lời đúng ( 2x³ - 3xy + 12x )( - 1/6xy ) bằng ?

   A. - 1/3x⁴y + 12x²y² - 2xy²

   B. - 1/3x⁴y + 1/2 x²y² + 2xy²

   C. - 1/3x⁴y + 12x²y² - 2x²y³

   D. - 1/3x⁴y + 1/2 x²y² - 2x²y

Lời giải:

Ta có: ( 2x³ - 3xy + 12x )( - 1/6xy )

= (- 1/6xy ). ( 2x³ - 3xy + 12x)

= ( - 1/6xy ).2x³ + (- 1/6xy).(-3xy) + (-1/6xy).12x

= - 1/3x⁴y + 1/2x²y² - 2x²y

Chọn đáp án D.

Bài 3: Biết 3x + 2( 5 - x ) = 0, giá trị của x cần tìm là ?

   A. x = -10   B. x =9

   C. x = - 8   D. x =0

Lời giải:

Ta có 3x + 2( 5 - x ) = 0 ⇔ 3x + 2.5 - 2.x = 0 ⇔ x + 10 = 0 ⇔ x = - 10.

Chọn đáp án A.

Bài 4: Kết quả nào sau đây đúng với biểu thức A = 2/5xy( x²y -5x + 10y ) ?

   A. 2/5x³y² + xy² + 2x²y.

   B. 2/5x³y² - 2x²y + 2xy².

   C. 2/5x³y² - 2x²y + 4xy².

   D. 2/5x³y² - 2x²y - 2xy².

Lời giải:

Ta có: A = 2/5xy( x²y -5x + 10y ) = 2/5xy .x²y - 2/5xy .5x + 2/5xy .10y

= 2/5x³y² - 2x²y + 4xy².

Chọn đáp án C.

Bài 5: Giá trị của x thỏa mãn 2x( x + 3 ) + 2( x + 3 ) = 0 là ?

   A. x = -3 hoặc x =1

   B. x =3 hoặc x = -1

   C. x = -3 hoặc x = -1

   D. x =1 hoặc x = 3

Lời giải:

Ta có 2x( x + 3 ) + 2( x + 3 ) = 0 ⇔ ( x + 3 )( 2x + 2 ) = 0

Chọn đáp án C.

Bài 6: Tính giá trị biểu thức 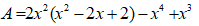tại x = 1

A. 2     B.3

C. 4     D. - 2

Lời giải:

Ta có:

Giá trị biểu thức A tại x = 1 là: A = 1⁴ – 3.1₃ + 4.1₂ = 1- 3 + 4 = 2.

Chọn đáp án A

Bài 7: Rút gọn biểu thức: A = 2x²(-3x³ + 2x² + x - 1) + 2x(x² – 3x + 1)

A. A = -6x⁵ + 4x² - 4x³ - 2x

B. A = -6x⁵ + 2x² + 4x³ + 2x

C. A = -6x⁵ - 4x² + 4x³ + 2x

D. A = -6x⁵ - 2x² + 4x³ - 2x

Lời giải:

Ta có:

A = 2x²(-3x³ + 2x² + x - 1) + 2x(x² – 3x + 1)

A = 2x².(-3x³) + 2x².2x² + 2x². x + 2x².(-1) + 2x.x² + 2x.(-3x) + 2x.1

A = -6x⁵ + 4x² + 2x³ - 2x² + 2x³ – 6x² + 2x

A = -6x⁵ - 4x² + 4x³ + 2x

Chọn đáp án C

Bài 8: Giải phương trình: 2x²(x + 2) - 2x(x² + 2) = 0

A. x = 0

B. x = 0 hoặc x = -1

C. x = 1 hoặc x = -1

D. x = 0 hoặc x = 1

Lời giải:

Ta có: 2x²(x + 2) - 2x(x² + 2) = 0

2x².x + 2x².2 - 2x.x² - 2x. 2 = 0

2x³ + 4x² – 2x³ – 4x = 0

4x² – 4x = 0

4x(x – 1) = 0

Do đó x = 0 hoặc x = 1

Chọn đáp án D

Bài 9: Giải phương trình sau:

Lời giải:

Chọn đáp án D

Bài 10: Cho biểu thức hai biểu thức. Tính A + B?

A. 8x⁵ + 7x⁴ - 10x³ + x²

B. 8x⁵ – 7x⁴ - 10x³ + 2x²

C. 8x⁵ + 6x⁴ + 10x³ + 2x²

D. 8x⁵ – 7x⁴ + 8x³ - x²

Lời giải:

* Ta có:

A = 2x².x³ + 2x².x² + 2x². (-2x) + 2x².1

A = 2x⁵ + 2x⁴ - 4x³ + 2x²

Và B = -3x³.(-2x² + 3x + 2)

B = -3x³.(-2x²) - 3x³. 3x - 3x³.2

B = 6x⁵ – 9x⁴ – 6x³

Suy ra:

A + B = 2x⁵ + 2x⁴ – 4x³ + 2x² + 6x⁵ – 9x⁴ – 6x³

A + B = 8x⁵ – 7x⁴ - 10x³ + 2x²

Chọn đáp án B

Bài 11: Chọn câu sai.

A. Giá trị của biểu thức ax(ax + y) tại x = 1; y = 0 là a².

B. Giá trị của biểu thức ay²(ax + y) tại x = 0; y = 1 là (1 + a)².

C. Giá trị của biểu thức -xy(x - y) tại x = -5; y = -5 là 0.

D. Giá trị của biểu thức xy(-x - y) tại x = 5; y = -5 là 0.

Lời giải

+) Thay x = 1; y = 0 vào biểu thức ax(ax + y) ta được 

a.1(a.1+0) = a.a = a² nên phương án A đúng

+) Thay x = 0, y = 1 vào biểu thức ay²(ax + y) ta được 

a.1²(a.0+1) = a.1 = a nên phương án B sai.

+) Thay x = −5, y = −5 vào biểu thức −xy(x − y) ta được 

−(−5)(−5)[−5−(−5)] = −25.0 = 0  nên phương án C đúng

+) Thay x = 5, y = −5 vào biểu thức xy(−x − y) ta được 

5.(−5)[−5−(−5)] = −25.0 = 0 nên phương án D đúng.

Đáp án cần chọn là: B

Bài 12: Rút gọn và tính giá trị của biểu thức

Lời giải

Ta có P = 5x² - [4x² - 3x(x - 2)]

= 5x² – (4x² – 3x² + 6x) = 5x² – (x² + 6x)

= 5x² – x² – 6x = 4x² – 6x

Thay 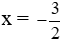 vào biểu thức P = 4x² – 6x ta được:

  

Vậy P = 4x² – 6x. Với 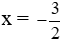 thì P = 18

Đáp án cần chọn là: A

Bài 13: Chọn câu đúng.

A. (x² – 1)(x² + 2x) = x⁴ – x³ – 2x      

B. (x² – 1)(x² + 2x) = x⁴ – x² – 2x

C. (x² – 1)(x² + 2x) = x⁴ + 2x³ – x² – 2x

D. (x² – 1)(x² + 2x) = x⁴ + 2x³ – 2x

Lời giải

Ta có: (x² – 1)(x² + 2x) = x².x² + x².2x – 1.x² – 1.2x

                                      = x⁴ + 2x³ – x² – 2x

Đáp án cần chọn là: C

Bài 14: Chọn câu đúng.

A. (x – 1)(x² + x + 1) = x³ – 1            

B. (x – 1)(x + 1) = 1 – x²

C. (x + 1)(x – 1) = x² + 1                   

D. (x² + x + 1)(x – 1) = 1 – x²

Lời giải

Ta có

+) (x – 1)(x + 1) = x.x + x – x – 1 = x² – 1 nên phương án B sai, C sai

+) (x – 1)(x² + x + 1)

= x.x² + x.x + x.1 – x² – x – 1

= x³ + x² + x – x² – x – 1 = x³ – 1 nên phương án D sai, A đúng

Đáp án cần chọn là: A

Bài 15: Chọn câu đúng.

A. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 17x – 1

B. (2x – 1)(3x² -7x + 5) = 6x³ – 4x² + 4x – 5

C. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 10x – 5

D. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 17x – 5

Lời giải

Ta có (2x – 1)(3x² -7x + 5) = 2x.3x² + 2x.(-7x) + 2x.5 – 3x² – (-7x) – 1.5

                                      = 6x³ – 14x² + 10x – 3x² + 7x – 5

                                      = 6x³ – 17x² + 17x – 5

Đáp án cần chọn là: D

Bài 16: Cho 4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14). Kết quả x bằng:

A. 8            

B. -8           

C. 6            

D. -6

Lời giải

Ta có

4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14)

⇔ 72 – 20x – 36x + 84 = 30x – 240 – 6x – 84

⇔ -56x + 156 = 24x – 324

⇔ 24x + 56x = 156 +324

⇔ 80x = 480

⇔ x = 6

Vậy x = 6

Đáp án cần chọn là: C

Bài 17: Cho 2x(3x – 1) – 3x(2x – 3) = 11. Kết quả x bằng:

Lời giải

Ta có:

Đáp án cần chọn là: D

Bài 18: Cho biểu thức P = 2x(x² – 4) + x²(x² – 9). Hãy chọn câu đúng:

A. Giá trị của biểu thức P tại x = 0 là 1

B. Giá trị của biểu thức P tại x = 2 là -20

C. Giá trị của biểu thức P tại x = -2 là 30

D. Giá trị của biểu thức P tại x = -9 là 0

Lời giải

Thay x = 0 vào P ta được

P = 2.0(0² – 4) + 0²(0² – 9) = 0 nên A sai.

Thay x = -2 vào P ta được

P = 2.(-2).((-2)² – 4) + (-2)².((-2)² – 9) = -20 nên C sai.

Thay x = -9 vào P ta được

P = 2.(-9).((-9)² – 4) + (-9)².((-9)² – 9) = 4446 nên D sai.

Thay x = 2 vào P ta được

P = 2.2.(2² – 4) + 2²(2² – 9) = 4.0 + 4.(-5) = -20 nên B đúng

Đáp án cần chọn là: B

Bài 19: Cho biểu thức M = x²(3x – 2) + x(-3x² + 1). Hãy chọn câu đúng

A. Giá trị của biểu thức M tại x = 0 là 1

B. Giá trị của biểu thức M tại x = 1 là 1

C. Giá trị của biểu thức M tại x = -2 là -6

D. Giá trị của biểu thức M tại x = 3 là -15

Lời giải

Ta có M = x²(3x – 2) + x(-3x² + 1) = x².3x + x².(-2) + x.(-3x²) + x.1

                                                    = 3x³ – 2x² – 3x³ + x = -2x² + x

Thay x = 0 vào M = -2x² + x ta được

M = -2.0² + 0 = 0 nên A sai.

Thay x = 1 vào M = -2x² + x ta được

M = -2.1² + 1 = -1 nên B sai

Thay x = -2 vào M = -2x² + x ta được

M = -2.(-2)² + (-2) = -10 nên C sai.

Thay x = 3 vào M = -2x² + x ta được

M = -2.3² + 3 = -15 nên D đúng

Đáp án cần chọn là: D

Bài 20: Cho biểu thức A = x(x + 1) + (1 – x)(1 + x) – x. Khẳng định nào sau đây là đúng.

A. A = 2 – x

B. A < 1     

C. A > 0     

D. A > 2

Lời giải

Ta có A = x(x + 1) + (1 – x)(1 + x) – x = x² + x + 1 + x – x – x² – x = 1

Suy ra A = 1 > 0

Đáp án cần chọn là: C

Bài 21: Kết quả của phép tính (x -2)(x +5) bằng ?

   A. x² - 2x - 10.

   B. x² + 3x - 10

   C. x² - 3x - 10.

   D. x² + 2x - 10

Lời giải:

Ta có ( x - 2 )( x + 5 ) = x( x + 5 ) - 2( x + 5 )

= x² + 5x - 2x - 10 = x² + 3x - 10.

Chọn đáp án B.

Bài 22: Thực hiện phép tính ( 5x - 1 )( x + 3 ) - ( x - 2 )( 5x - 4 ) ta có kết quả là ?

   A. 28x - 3.

   B. 28x - 5.

   C. 28x - 11.

   D. 28x - 8.

Lời giải:

Ta có ( 5x - 1 )( x + 3 ) - ( x - 2 )( 5x - 4 ) = 5x( x + 3 ) - ( x + 3 ) - x( 5x - 4 ) + 2( 5x - 4 )

= 5x² + 15x - x - 3 - 5x² + 4x + 10x - 8 = 28x - 11

Chọn đáp án C.

Bài 23: Giá trị của x thỏa mãn ( x + 1 )( 2 - x ) - ( 3x + 5 )( x + 2 ) = - 4x² + 1 là ?

   A. x = - 1.

   B. x = - 9/10

   C. x = - 3/10.

   D. x = 0

Lời giải:

Ta có ( x + 1 )( 2 - x ) - ( 3x + 5 )( x + 2 ) = - 4x² + 1

⇔ ( 2x - x² + 2 - x ) - ( 3x² + 6x + 5x + 10 ) = - 4x² + 1

⇔ - 4x² - 10x - 8 = - 4x² + 1 ⇔ - 10x = 9 ⇔ x = - 9/10

Vậy giá trị x cần tìm là x = - 9/10.

Chọn đáp án B.

Bài 24: Biểu thức rút gọn của biểu thức A = ( 2x - 3 )( 4 + 6x ) - ( 6 - 3x )( 4x - 2 ) là ?

A. 0   

B. 40x

C. - 40x   

D. Kết quả khác.

Lời giải:

Ta có A = ( 2x - 3 )( 4 + 6x ) - ( 6 - 3x )( 4x - 2 )

= ( 8x + 12x² - 12 - 18x ) - ( 24x - 12 - 12x² + 6x )

= 12x² - 10x - 12 - 30x + 12x² + 12 = 24x² - 40x.

Chọn đáp án D.

Bài 25: Rút gọn biểu thức A = (x + 2).(2x - 3) + 2 ta được:

A. 2x² + x - 4     B. x² + 4x - 3

C. 2x² – 3x + 2     D. –2x² + 3x -2

Lời giải:

Ta có: A = (x + 2).(2x - 3) + 2

A = x.(2x – 3) + 2. (2x – 3) + 2

A = 2x² – 3x + 4x - 6 + 2

A = 2x² + x – 4

Chọn đáp án A

Bài 26: Rút gọn biểu thức A = (2x² + 2x).(-2x² + 2x ) ta được:

A. 4x⁴ + 8x³ + 4x²     B. –4x⁴ + 8x³

C. –4x⁴ + 4x²     D. 4x⁴ - 4x²

Lời giải:

Ta có: A = (2x² + 2x).(-2x² + 2x )

A = 2x².(-2x² + 2x) + 2x.(-2x² + 2x)

A = 2x².(-2x²) + 2x².2x + 2x. (-2x²) + 2x .2x

A = -4x⁴ + 4x³ - 4x³ + 4x²

A = -4x⁴ + 4x²

Chọn đáp án C

Bài 27: Biểu thức A bằng ?

Lời giải:

Ta có:

Chọn đáp án B

Bài 28: Tính giá trị biểu thức: A = (x + 3).(x² – 3x + 9) tại x = 10

A. 1980    

B. 1201

C. 1302    

D.1027

Lời giải:

Ta có: A = (x + 3).(x² – 3x + 9)

A = x .(x² – 3x + 9) + 3.(x² – 3x + 9)

A = x³ – 3x² + 9x + 3x² – 9x + 27

A = x³ + 27

Giá trị biểu thức khi x = 10 là : A = 10³ + 27 = 1027

Chọn đáp án D

Bài 29: Tìm x biết: (2x + 2)(x - 1) – (x + 2).(2x + 1) = 0

Lời giải:

Ta có: (2x + 2)(x - 1) – (x + 2).(2x + 1) = 0

⇔ 2x.(x - 1) + 2(x - 1) - x(2x + 1) – 2.(2x +1)= 0

⇔ 2x² – 2x + 2x – 2 - 2x² – x - 4x – 2 = 0

⇔ - 5x - 4 = 0

⇔ - 5x = 4

⇔ x = -4/5

Chọn đáp án A

Bài 30: Tìm x biết: (3x + 1). (2x- 3) - 6x.(x + 2) = 16

A. x = 2     B. x = - 3

C. x = - 1     D. x = 1

Lời giải:

Ta có:

⇔ (3x + 1).(2x - 3) - 6x.(x + 2) = 16

⇔ 3x(2x - 3) + 1.(2x – 3 ) - 6x. x – 6x . 2 = 16

⇔ 6x² – 9x + 2x – 3 – 6x² - 12x = 16

⇔ -19x = 16 + 3

⇔ - 19x = 19

⇔ x = - 1

Chọn đáp án C

Bài 31: Cho các số x, y, z tỉ lệ với các số a, b, c. Khi đó (x² + 2y² + 3z²)(a² + 2b² + 3c²) bằng

A. ax + 2by + 3cz 

B. (2ax + by + 3cz)²

C. (2ax + 3by + cz)²

D. (ax + 2by + 3cz)²

Lời giải

Vì x, y, z tỉ lệ với các số a, b, c nên 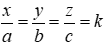 suy ra x = ka, y = kb, z = kc

Thay x = ka, y = kb, z = kc vào (x² + 2y² + 3z²)(a² + 2b² + 3c²) ta được

[(ka)² + 2(kb)² + 3(kc)²](a² + 2b² + 3c²)

= (k²a² + 2k²b² + 3k²c²)(a² + 2b² + 3c²)

= k²(a² + 2b² + 3c²)(a² + 2b² + 3c²)

= k²(a² + 2b² + 3c²)² = [k((a² + 2b² + 3c²)]²

= (ka² + 2kb² + 3kc²)²

= (ka.a + 2kb.b + 3kc.c)²

= (xa + 2yb + 3zc)² do x = ka,y = kb, z = kc

Vậy (x² + 2y² + 3z²)(a² + 2b² + 3c²) = (ax + 2by + 3cz)²

Đáp án cần chọn là: D

Bài 32: Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.

A. B ⁝ 10 với mọi m Є Z          

B. B ⁝ 15 với mọi m Є Z 

C. B ⁝ 9 với mọi m Є Z            

D. B ⁝ 20 với mọi m Є Z 

Lời giải

Ta có B = (m – 1)(m + 6) – (m + 1)(m – 6)

          = m² + 6m – m – 6 – (m² – 6m + m – 6)

          = m² + 5m – 6 – m² + 6m – m + 6 = 10m

Nhận thấy 10 ⁝ 10 ⇒ 10.m ⁝ 10 nên B ⁝ 10 với mọi giá trị nguyên của m.

Đáp án cần chọn là: A

Bài 33: Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó

Lời giải

+ Tổng của m số mà mỗi số bằng 3n – 1 là m(3n – 1)

+ Tổng của n số mà mỗi số bằng 9 – 3m là n(9 – 3m)

Tổng tất cả các số trên là m(3n – 1) + n(9 – 3m)

Theo đề bài ta có

m(3n – 1) + n(9 – 3m) = 5(m + n)

⇔ 3mn – m + 9n – 3mn = 5m + 5n

⇔ 6m = 4n ⇔ 

Vậy 

Đáp án cần chọn là: A

Bài 34: Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân (x² + x + 1)(x³ – 2x + 1)

A. 1            

B. -2           

C. – 3         

D. 3

Lời giải

Ta có (x² + x + 1)(x³ – 2x + 1)

          = x².x³ + x².(-2x) + x².1 + x.x³ + x.(-2x) + x.1 + 1.x³  + 1.(-2x) + 1.1

          = x⁵ – 2x³ + x² + x⁴ – 2x² + x + x³ – 2x + 1

          = x⁵ + x⁴ – x³ – x² – x + 1

Hệ số của lũy thừa bậc ba là – 1

Hệ số của lũy thừa bậc hai là – 1

Hệ số của lũy thừa bậc nhất là – 1

Tổng các hệ số này là -1 +(-1) + (-1) = -3

Đáp án cần chọn là: C

Bài 35: Nếu a + b = m và ab = n thì

A. (x + a)(x + b) = x² + mx + n 

B. (x + a)(x + b) = x² + nx + m

C. (x + a)(x + b) = x² – mx – n 

D. (x + a)(x + b) = x² – mx + n

 

Xem thêm Phương pháp giải các dạng Toán lớp 8 hay, chi tiết khác:

Phương pháp giải Những hằng đẳng thức đáng nhớ

Phương pháp giải Các phương pháp phân tích đa thức thành nhân tử

Phương pháp giải Cách chia đơn thức cho đơn thức, chia đa thức cho đơn thức

Phương pháp giải Cách chia đa thức một biến đã sắp xếp

Phương pháp giải Góc trong tứ giác