Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Mệnh đề phủ định (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải Mệnh đề phủ định (HAY NHẤT 2024)

1. Lý thuyết

Cho mệnh đề P.

- Mệnh đề “ không phải P ” được gọi là mệnh đề phủ định của P và kí hiệu là $\overline{P}$

- Nếu P đúng thì $\overline{P}$ sai, nếu P sai thì $\overline{P}$ đúng.

2. Phương pháp giải

- Phủ định của mệnh đề P là mệnh đề “ không phải P”.

- Phủ định của quan hệ = là quan hệ $\ne$ và ngược lại.

- Phủ định của quan hệ > là quan hệ $\le$ và ngược lại.

- Phủ định của quan hệ < là quan hệ $\ge$ và ngược lại.

- Phủ định liên kết “và” là liên kết “hoặc” và ngược lại.

- Mệnh đề phủ định của “$\forall x\in X;P\left(x\right)$” là: “$\exists x\in X;\overline{P\left(x\right)}$”.

- Mệnh đề phủ định của “$\exists x\in X;\overline{P\left(x\right)}$” là “$\forall x\in X;P\left(x\right)$”.

3. Ví dụ minh họa

Ví dụ 1: Phát biểu mệnh đề phủ định của các mệnh đề sau:

a. P: “ Mọi hình thoi là hình vuông”.

b. P: “ Số chính phương có thể có chữ số tận cùng là 0; 1; 4; 5; 6; 9 ”.

c. P: “ Đường thẳng đi qua một điểm và vuông góc với đường thẳng cho trước là duy nhất”.

Hướng dẫn:

a. $\overline{P}$: “ Tồn tại hình thoi không là hình vuông”.

b. $\overline{P}$: “ Số chính phương không thể có chữ số tận cùng là 0; 1; 4; 5; 6; 9 ”.

c. $\overline{P}$: “ Đường thẳng đi qua một điểm và vuông góc với đường thẳng cho trước không là duy nhất”.

Ví dụ 2: Xét xem các mệnh đề sau đúng hay sai, lập mệnh đề phủ định của mệnh đề:

a.$\forall x\in ℝ,x^2-x+1>0$.

b.$\exists n\in \mathbb{N},(n+2)(n+1)=0$.

c.$\exists x\in \mathbb{Q},x^2=3$.

Hướng dẫn:

a. Mệnh đề đúng, vì $x^2-x+1={\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}>0,\forall x$.

    Mệnh đề phủ định là $\exists x\in ℝ,x^2-x+1\le 0$.

b. Mệnh đề sai, vì $(n+2)(n+1)=0\Rightarrow$n = -2 hoặc n = -1 đều không thuộc N.

    Mệnh đề phủ định là $\forall n\in \mathbb{N},(n+2)(n+1)\ne 0$.

c. Mệnh đề sai, vì $x^2=3\Rightarrow x=\pm \sqrt{3}\notin \mathbb{Q}$.

   Mệnh đề phủ định là $\forall x\in \mathbb{Q},x^2\ne 3$.

Ví dụ 3: Nêu mệnh đề phủ định của mệnh đề: “$\forall n\in \mathbb{N},n^2+1$ không chia hết cho 3”.

Hướng dẫn:

Phủ định của $\forall$ là $\exists$. Phủ định của “không chia hết” là “chia hết”.

Mệnh đề phủ định của mệnh đề “$\forall n\in \mathbb{N},n^2+1$ không chia hết cho 3” là:

“$\exists n\in \mathbb{N},n^2+1$ chia hết cho 3”.

4. Bài tập vận dụng

Câu 1: Chọn khẳng định sai:

A. Cho mệnh đề P và mệnh đề phủ định $\overline{P}$, nếu P đúng thì $\overline{P}$ sai và điều ngược lại chắc đúng.

B. Mệnh đề P và mệnh đề phủ định $\overline{P}$ cùng đúng hoặc cùng sai.

C. Mệnh đề phủ định của mệnh đề P là mệnh đề “ không phải P” được kí hiệu là .$\overline{P}$

D. Mệnh đề : “ $\mathrm{\pi }$ là số hữu tỷ” khi đó mệnh đề phủ định $\overline{P}$ là: “ $\mathrm{\pi }$ là số vô tỷ”.

Hướng dẫn:

Chọn B. Theo lý thuyết nếu P đúng thì $\overline{P}$ sai và ngược lại

Câu 2: Phủ định của mệnh đề: “ Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

Hướng dẫn:

Chọn C.

Phủ định của “có ít nhất” là “mọi”.

Phủ định của “tuần hoàn” là “không tuần hoàn”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: “Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn”.

Câu 3: Cho mệnh đề A “$\forall x\in ℝ,x^2-x+7<0$”. Mệnh đề phủ định $\overline{A}$ của mệnh đề A là:

A. $\forall x\in ℝ,x^2-x+7>0$.

B. $\forall x\in ℝ,x^2-x+7\ge 0$.

C. Không tồn tại $x:x^2-x+7<0$.     

D. $\exists x\in ℝ,x^2-x+7\ge 0$.

Hướng dẫn:

Chọn D.

Theo lý thuyết, mệnh đề phủ định của “$\forall x\in X;P\left(x\right)$” là: “$\exists x\in X;\overline{P\left(x\right)}$”.

Vậy mệnh đề phủ định $\overline{A}$ của mệnh đề A là: $\exists x\in ℝ,x^2-x+7\ge 0$.

Câu 4: Mệnh đề phủ định của mệnh đề  “$\exists x:x^2+2x+5$ là số nguyên tố” là :

A. $\forall x:x^2+2x+5$ không là số nguyên tố.  

B. $\exists x:x^2+2x+5$ là hợp số.

C. $\forall x:x^2+2x+5$ là hợp số.

D. $\exists x:x^2+2x+5$ là số thực.

Hướng dẫn :

Chọn A.

Phủ định của  $\exists$ là $\forall$.

Phủ định của “ là số nguyên tố” là “ không là số nguyên tố”.

Vậy mệnh đề phủ định $\overline{P}$ của mệnh đề P là :$\forall x:x^2+2x+5$ không là số nguyên tố.

Câu 5: Mệnh đề nào sau đây là phủ định của mệnh đề: “ Mọi phương trình đều có nghiệm”

A.  Mọi phương trình đều vô nghiệm.

B. Tất cả các phương trình đều không có nghiệm.

C. Có ít nhất một phương trình vô nghiệm.

D. Có duy nhất một phương trình vô nghiệm.

Hướng dẫn:

Chọn C.

Phủ định của “mọi” là “có ít nhất”.

Phủ định của “vô nghiệm” là “có nghiệm”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: Có ít nhất một phương trình vô nghiệm.

Câu 6: Mệnh đề phủ định của mệnh đề P: “$\exists x\in ℝ,5x-3x^2=1$” là:

A. $\exists x\in ℝ,5x-3x^2$.                 

B. $\forall x\in ℝ,5x-3x^2=1$.

C. $\forall x\in ℝ,5x-3x^2\ne 1$. 

D. $\exists x\in ℝ,5x-3x^2\ge 1$.

Hướng dẫn:

Chọn C.

Phủ định của $\exists$  là $\forall$.

Phủ định của = là $\ne$.

Vậy mệnh đề phủ định $\overline{P}$ của mệnh đề P là : $\forall x\in ℝ,5x-3x^2\ne 1$.

Câu 7: Cho mệnh đề $P\left(x\right):"\forall x\in ℝ,x^2+x+1>0"$. Mệnh đề phủ định của mệnh đề $P\left(x\right)$ là:

A. $\forall x\in ℝ,x^2+x+1<0$.

B. $\forall x\in ℝ,x^2+x+1\le 0$.

C. $\exists x\in ℝ,x^2+x+1\le 0$.

D. $\cancel{\exists }x\in ℝ,x^2+x+1>0$.

Hướng dẫn:

Chọn C.

Phủ định của $\forall$ là $\exists$.

Phủ định của > là $\le$.

Vậy mệnh đề phủ định của mệnh đề $P\left(x\right)$ là: $\exists x\in ℝ,x^2+x+1\le 0$.

Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phủ định của mệnh đề “$\forall x\in ℝ,\frac{x^2}{2x^2+1}<\frac{1}{2}$” là mệnh đề “$\exists x\in ℝ,\frac{x^2}{2x^2+1}>\frac{1}{2}$”.

B. Phủ định của mệnh đề “$\forall k\in \mathbb{Z},k^2+k+1$ là một số lẻ” là mệnh đề “$\exists k\in \mathbb{Z},k^2+k+1$là một số chẵn”.

C. Phủ định của mệnh đề “$\forall n\in \mathbb{N}$ sao cho $n^2-1$ chia hết cho 24” là mệnh đề “ $\forall n\in \mathbb{N}$ sao cho $n^2-1$ không chia hết cho 24”.

D. Phủ định của mệnh đề “$\forall x\in \mathbb{Q},x^3-3x+1>0$” là mệnh đề “$\forall x\in \mathbb{Q},x^3-3x+1\le 0$”.

Hướng dẫn:

Chọn B: vì phủ định của $\forall$ là $\exists$, phủ định của số lẻ là số chẵn.

Đáp án A sai vì phủ định của < phải là $\ge$.

Đáp án C sai vì phủ định của $\forall$ phải là $\exists$.

Đáp án D sai vì phủ định của $\forall$ phải là $\exists$.

Câu 9: Mệnh đề phủ định của mệnh đề “ Có ít nhất một số thực x thỏa mãn điều kiện bình phương của nó là 1 số không dương” là:

A. $\forall x\in ℝ:x^2>0$.

B.$\exists x\in ℝ:x^2\le 0$ .

C. $\forall x\in ℝ:x^2\le 0$.

D. $\exists x\in ℝ:x^2>0$.

Hướng dẫn:

Chọn A.

Theo giả thiết, ta có mệnh đề P: $"\exists x\in ℝ:x^2\le 0"$.

Vậy mệnh đề phủ định $\overline{P}$ của mệnh đề P là: $\forall x\in ℝ:x^2>0$.

Câu 10: Cho mệnh đề “ Phương trình $x^2-4x+4=0$ có nghiệm”. Mệnh đề phủ định của mệnh đề đã cho và tính đúng, sai của mệnh đề phủ định là:

A. Phương trình $x^2-4x+4=0$ có nghiệm. Đây là mệnh đề đúng. 

B. Phương trình $x^2-4x+4=0$ có nghiệm. Đây là mệnh đề sai.

C. Phương trình $x^2-4x+4=0$ vô nghiệm. Đây là mệnh đề đúng.

D. Phương trình $x^2-4x+4=0$ vô nghiệm. Đây là mệnh đề sai.

Hướng dẫn :

Chọn D. 

Phủ định của “có nghiệm” là “vô nghiệm”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: Phương trình $x^2-4x+4=0$ vô nghiệm.

Mệnh đề phủ định sai do phương trình $x^2-4x+4=0$ có nghiệm là 2.

5. Bài tập tự luyện 

Bài 1:Trong các câu dưới đây, câu nào là mệnh đề, câu nào không phải là mệnh đề. Nếu là mệnh đề thì hãy xét xem nó đúng hay sai:

a) x² + x + 1 > 0

b) 26 chia hết cho 2 và cho 13

c) x² + y² > 9

d) x – 2y và 2 xy

Bài 2:

Các mệnh đề dưới đây thuộc mệnh đề gì và hãy nói nó đúng hay sai:

a) Nếu số a chia hết cho 3 thì a chia hết cho 6.

b) Nếu Δ ABC cân tại A thìΔABC có AB = AC.

c) Tứ giác ABCD là hình vuông khi và chỉ khi ABCD là hình chữ nhật và có AC vuông góc với BD.

Bài 3. Xét các mệnh đề P: “x là một số hữu tỉ” và Q: “x² là một số hữu tỉ”.

a) Phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề trên.

c) Chỉ ra một giá trị của x mà mệnh đề đảo sai.

Bài 4. Phát biểu phủ định của mệnh đề sau và xét tính đúng sai của nó:

a) P: “15 không chia hết cho 3”;

b) Q: “$\sqrt{2}>1$”.

Bài 5. Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của chúng:

a) P(x): “$\forall x\in ℝ,x^2>0$” ;

b) Q(n): “$\exists n\in \mathbb{N},2n+5<2$”.

Bài 6: Xét xem các mệnh đề sau đây đúng hay sai và nêu mệnh đề phủ định của mỗi mệnh đề đó:

a)∀n ∈ N^* , n (n² - 1 ) là bội số của 3.

b)∀x ∈ R, x² - 6x + 15 > 0

c) ∃x ∈ R: x² - 6x + 5 = 0

d)∀x ∈ R ,∃y ∈ R:y = x + 3

e)∀x ∈ R ;∀y ∈ R: 

f) ∃n ∈ N ,2ⁿ - 1 là số nguyên tố.

Bài 7: Phát biểu dưới dạng "điều kiện cần" đối với các mệnh đề sau:

a) Hai góc đối đỉnh thì bằng nhau.

b) Hai tam giác có hai cặp cạnh bằng nhau kèm giữa một cặp góc bằng nhau thì bằng nhau.

c) Hai tam giác có hai cặp góc bằng nhau thì bằng nhau.d) Một số chia hết cho 3 khi và chỉ khi tổng các chữ số chia hết cho 3.

Bài 8: Cho biết tính đúng, sai của các mệnh đề sau. Nếu sai, hãy sửa lại cho đúng:

a) ΔABC đều ⇔ Tam giác có ít nhất một góc bằng 60⁰ .

b) 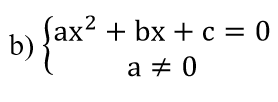 có nghiệm kép

⇔Δ=b²-4ac=0.

c) ΔABC cân tại A ⇔ Hai đường cao BE và CF bằng nhau.

d) ∀a,b,c ∈ R: 

e) ∀a,b ∈ R: .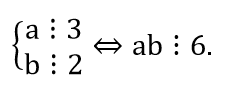

Bài 9: Cho tứ giác ABCD, xét hai mệnh đề:

P: " ABCD có tổng hai góc đối bằng 180°"

Q: " ABCD là tứ giác nội tiếp."

Phát biểu mệnh đề P ⇒ Q và cho biết tính đúng, sai của mệnh đề.

Bài 10: Cho ΔABC, xét hai mệnh đề:

P: "ΔABC vuông cân tại A"

Q: "ΔABC là tam giác vuông có AB =AC"

Phát biểu mệnh đề P ⇔ Q bằng hai cách và cho biết mệnh đề này đúng hay sai.

Bài 11: Cho mệnh đề chứa biến P(n): "n(n+1) là số lẻ" với n là số nguyên. Hãy phát biểu các mệnh đề:

a) "∀n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

b) "∃n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

Xác định tính đúng sai của mệnh đề

Mệnh đề và suy luận toán học hay và chi tiết

Tập hợp, cách xác định tập hợp và cách giải bài tập

Các phép toán trên tập hợp và cách giải bài tập

Các bài toán về các tập hợp số và cách giải