Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các bài toán về các tập hợp số (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Nội dung bài viết
Phương pháp giải Các bài toán về các tập hợp số (HAY NHẤT 2024)
1. Lý thuyết
- Tập hợp con của R: ℕ⊂ℤ⊂ℚ⊂ℝ. Trong đó:
N: là tập hợp số tự nhiên.
Z : là tập hợp số nguyên.
Q : là tập hợp số hữu tỷ.
ℝ=(−∞;+∞): là tập hợp số thực.
- Các tập hợp con thường dùng của R
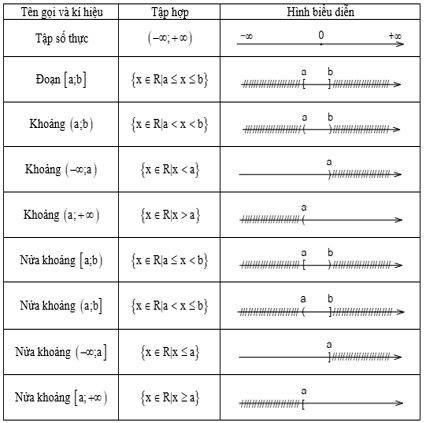
2. Phương pháp giải
Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.
3. Ví dụ minh họa
Ví dụ 1: Xác định mỗi tập hợp sau và biểu diễn nó trên trục số.
a. (−3;3)∪(−1;0).
b. (−1;3)∪[0;5].
c. (−2;2]∩[1;3).
Hướng dẫn:
Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.
a. (−3;3)∪(−1;0) = (-3; 3).
![]()
b.(−1;3)∪[0;5] = (-1; 5].
![]()
c. (−2;2]∩[1;3) = [1; 2]
![]()
Ví dụ 2: Cho các tập hợp :
A={x∈ℝ|−3≤x≤2}
B={x∈ℝ|0<x≤7}
C={x∈ℝ|x<−1}
D={x∈ℝ|x≥5}
Hãy dùng kí hiệu đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên.
Hướng dẫn:
- Theo lý thuyết: [a;b]={x∈ℝ| a≤x≤b}
Vậy A={x∈ℝ|−3≤x≤2}= [-3; 2].
- Theo lý thuyết: (a;b]={x∈ℝ| a<x≤b}.
Vậy B={x∈ℝ|0<x≤7} = (0; 7].
- Theo lý thuyết: (−∞;b)={x∈ℝ| x<b}.
Vậy C={x∈ℝ|x<−1} = (−∞;−1).
- Theo lý thuyết: [a;+∞)={x∈ℝ| a≤x}.
Vậy D={x∈ℝ|x≥5} = [5;+∞).
Ví dụ 3: Cho hai tập hợp A={x∈ℝ|−5≤x<1};B={x∈ℝ|−3<x≤3}. Tìm A∩B
Hướng dẫn:
Ta có: A={x∈ℝ|−5≤x<1} = [-5; 1) ( theo lý thuyết: [a;b)={x∈ℝ| a≤x<b})
B={x∈ℝ|−3<x≤3}= (-3; 3] ( theo lý thuyết: (a;b]={x∈ℝ| a<x≤b} )
Ta biểu diễn tập hợp A và B trên trục số như sau:
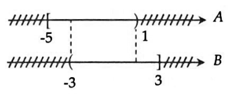
Vậy A∩B = (-3; 1).
4. Bài tập vận dụng
Câu 1: Cho tập hợp A={x∈ℝ|−3<x<1}. Tập A là tập nào sau đây?
A.{-3; 1}.
B. [-3; 1].
C. [-3; 1).
D. (-3; 1).
Hướng dẫn:
Chọn D.
Theo lý thuyết: (a;b)={x∈ℝ| a<x<b}
Vậy A={x∈ℝ|−3<x<1}= (-3; 1).
Câu 2: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
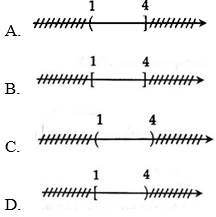
Hướng dẫn:
Chọn A. Vì (1; 4] gồm các số thực x mà 1<x≤4
Đáp án B sai vì [1; 4] gồm các số thực x mà 1≤x≤4.
Đáp án C sai vì (1; 4) gồm các số thực x mà 1 < x < 4.
Đáp án B sai vì [1; 4) gồm các số thực x mà 1≤x<4.
Câu 3: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A={x∈ℝ|4≤x≤9}:
A. A = [4; 9].
B. A = (4; 9].
C. A = [4; 9).
D. A = (4; 9)
Hướng dẫn:
Chọn A.
Theo lý thuyết: [a;b]={x∈ℝ| a≤x≤b}. Suy ra A={x∈ℝ|4≤x≤9}= [4; 9] .
Câu 4: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A∪B.
A. (1; 7).
B. [-2; 9].
C. [-2; 1).
D. (7; 9].
Hướng dẫn:
Chọn B.
Ta biểu diễn tập hợp A và B trên trục số như sau:
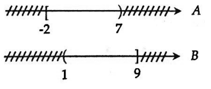
Vậy A∪B = [−2;7)∪(1;9]=[−2;9]
Câu 5: Cho tập hợp X={x|x∈ℝ,1≤|x|≤3} thì X được biểu diễn là hình nào sau đây?
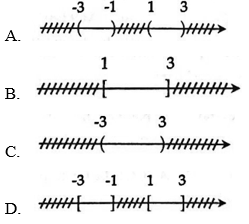
Hướng dẫn:
Chọn D.
Giải bất phương trình:
1≤|x|≤3⇔{|x|≥1|x|≤3⇔{[x≥1x≤−1−3≤x≤3⇔[{x≥1−3≤x≤3{x≤−1−3≤x≤3⇔[1≤x≤3−3≤x≤−1⇔x∈[−3;−1]∪[1;3]
Vậy đáp án D thỏa mãn x∈[−3;−1]∪[1;3].
Câu 6: Cho hai tập hợp A = (1; 5]; B = (2; 7]. Tập hợp A \ B là:
A. (1; 2].
B. (2; 5).
C. (-1; 7].
D. (-1; 2).
Hướng dẫn:
Chọn A.
Ta biểu diễn tập hợp A và B trên trục số:
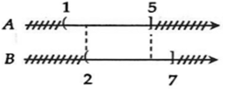
Vậy A \ B = {x∈ℝ| x∈A và x∉B}⇒x∈(1;2]
Câu 7: Cho các số thực a, b, c, d và a < b < c < d. Khẳng định nào sau đây là đúng?
A. (a;c)∩(b;d)=(b;c)
B. (a;c)∩(b;d)=(b;c]
C. (a;c)∩(b;d)=[b;c)
D. (a;c)∪(b;d)=[b;c]
Hướng dẫn:
Chọn A.
Ta biểu diễn (a; c); (b; d) trên trục số sau đó dựa vào tính chất giao của hai tập hợp để tìm ra đáp án:
![]()
Vậy (a;c)∩(b;d)=(b;c).
Câu 8: Cho tập hợp A = [m; m+2]; B = [-1; 2]. Tìm điều kiện của m để A⊂B.
A.m≤−1 hoặc m≥0.
B. −1≤m≤0
C. 1≤m≤2
D. m < 1 hoặc m > 2.
Hướng dẫn:
Chọn B.
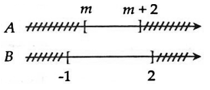
Điều kiện để A⊂B là: −1≤m<m+2≤2.
⇔{m≥−1m+2≤2⇔{m≥−1m≤0⇔−1≤m≤0
Câu 9: Cho hai tập hợp A = [-2; 3]; B = (m; m+6). Điều kiện để A⊂B là:
A. −3≤m≤−2
B. −3<m<−2
C. m<−3
D.m≥−2
Hướng dẫn:
Chọn B.
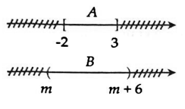
Điều kiện để A⊂B là :
m<−2<3<m+6⇔{m<−2m+6>3⇔{m<−2m>−3⇔−3<m<−2
Câu 10: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a≤4 để X∩Y≠∅.
A. [a<3a≥4.
B. a < 3.
C. a < 0.
D. a > 3.
Hướng dẫn:
Chọn B.
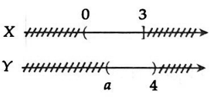
Xét:
X∩Y=∅⇒{a≥3a≤4⇔3≤a≤4
⇒X∩Y≠∅⇔[a<3a>4.Mà theo đề bài,a≤4 nên suy ra a < 3.
Vậy với a < 3 thì X∩Y≠∅.
5. Bài tập tự luyện
Bài 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó
a) A={x ∈ R|(2x2 - 5x + 3)(x2 - 4x + 3)= 0}.
b) B={x ∈ R|(x2 - 10x + 21)(x3 - x)= 0}.
c) C={x ∈ N|x + 3 < 4 + 2x; 5x - 3 < 4x - 1}.
d) D={x ∈ Z||x + 2| ≤ 3}.
e) E={x ∈ R|x2 + x + 3 = 0}.
Bài 2: Viết các tập sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {0; 1; 2; 3; 4}
b) B ={ -3; 9; -27; 81}
e) E = Tập tất cả các điểm thuộc đường trung trực của đoạn thẳng AB.
f) F = Tập tất cả các điểm thuộc đường tròn tâm I cho trước và có bán kính bằng 5.
Bài 3: Cho biết mỗi tập hợp sau có bao nhiêu tập hợp con, tìm tất cả các tập hợp con của tập hợp sau:
a) A = {1; 2}
b) B = {1; 2; 3}
c) C={x ∈ R|2x2-5x+2=0}
d) D={x ∈ Q|x2-4x+2=0}
Bài 4: Trong các tập hợp sau, tập nào là tập con của tập nào?
a)
| A = {1; 2; 3}, | B ={x ∈ N|x < 4}, |
| C ={0; +∞}, | D ={x ∈ R|2x2 - 7x + 3 = 0} |
b)
| A = Tập các ước số tự nhiên của 6; | B = Tập các ước số tự nhiên của 12; |
c)
| A = Tập các hình bình hành; | B = Tập các hình chữ nhật; |
| C = Tập các hình thoi; | D = Tập các hình vuông, |
d)
| A = Tập các tam giác cân; | B = Tập các tam giác đều; |
| C = Tập các tam giác vuông; | D = Tập các tam giác vuông cân. |
Bài 5: Tìm A ∩ B;A ∪ B;A\B;B\A với
a) A={2,4,7,8,9,12};B={2,8,9,12}.
b) A={x ∈ Q|2x2 - 3x + 1 = 0};B={x ∈ R||2x - 1|= 1}
c) A = Tập các ước số của 12; B = Tập hợp các ước số của 18.
d) A={x ∈ N|(x2 - 9)(x2 - 5x + 6 = 0}; B = Tập các số nguyên tố có 1 chữ số.
Bài 6: Xác định các tập hợp A, B sao cho:
A ∩ B ={0,1,2,3,4}; A \ B ={-3,-2};B \ A ={6,9,10}.
Bài 7: Mỗi học sinh lớp 10A đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn thể thao này. Hỏi lớp 10A có bao nhiêu học sinh?
Bài 8: Kết quả điều tra ở một lớp cho thấy: có 20 hoc sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích chơi bóng chuyền, 14 học sinh thích bóng đá và bơi, 13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền, 10 học sinh thích cả ba môn, 12 học sinh không thich môn nào. Tính xem lơp học có bao nhiêu học sinh?
Bài 9: Trong 100 học sinh lớp 10, có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được cả hai tiếng Anh và Pháp
Bài 10: Cho các tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 2, 3, 4};
C = {2, 4, 6, 8}. Hãy xác định: CA B; CA C;CA (B ∪ C).
Xem thêm các dạng Toán 10 hay, chọn lọc khác:
Các phép toán trên tập hợp và cách giải bài tập
Các bài toán về Số gần đúng và sai số và cách giải
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.