Toptailieu.vn biên soạn và giới thiệu Công thức giải phương trình bậc hai (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức giải phương trình bậc hai (50 bài tập minh họa) HAY NHẤT 2024

I. Lí thuyết tổng hợp

- Phương trình bậc hai có dạng ${\text{ax}}^2+bx+c=0$ ($a\ne 0$)

- Cách giải và biện luận phương trình bậc hai:

+ Với $\Delta =b^2-4ac$

Nếu $\Delta >0$ thì phương trình bậc hai có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}$,$x_2=\frac{-b-\sqrt{\Delta }}{2a}$

Nếu $\Delta =0$ thì phương trình bậc hai có nghiệm kép: $x_1=x_2=\frac{-b}{2a}$

Nếu $\Delta <0$ thì phương trình bậc hai vô nghiệm.

+ Với $\Delta \text{'}=b{\text{'}}^2-ac$ với $b\text{'}=\frac{b}{2}$

Nếu $\Delta \text{'}>0$ thì phương trình bậc hai có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}$,$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}$

Nếu $\Delta \text{'}=0$ thì phương trình bậc hai có nghiệm kép:$x_1=x_2=\frac{-b\text{'}}{a}$

Nếu $\Delta \text{'}<0$ thì phương trình bậc hai vô nghiệm.

- Đối với các phương trình quy về phương trình bậc hai ta có thể dùng các phép biến đổi như nhân đa thức, quy đồng mẫu số, chuyển vế, lấy nhân tử chung … để đưa phương trình đã cho về dạng $$${\text{ax}}^2+bx+c=0$ ($a\ne 0$).

II. Các công thức

- Giải và biện luận phương trình bậc hai ${\text{ax}}^2+bx+c=0$ ($a\ne 0$):

+ Với $\Delta =b^2-4ac$

$$\begin{gathered} \Delta >0\Rightarrow {\text{ax}}^2+bx+c=0 \\ \iff \left[\begin{array}{l}{x}_1=\frac{{\displaystyle -b+\sqrt{\Delta }}}{{\displaystyle 2a}}\\ x_2=\frac{{\displaystyle -b-\sqrt{\Delta }}}{{\displaystyle 2a}}\end{array}\right. \\ \Delta =0\Rightarrow {\text{ax}}^2+bx+c=0 \\ \iff x_1=x_2=\frac{{\displaystyle -b}}{{\displaystyle 2a}} \\ \Delta <0\Rightarrow {\text{\hspace{0.17em}ax}}^2+bx+c=0 \\ \iff x\in \varnothing \end{gathered}$$

+ Với  $\Delta \text{'}=b{\text{'}}^2-ac\left(b\text{'}=\frac{b}{2}\right)$

$$\begin{gathered} \Delta \text{'}>0\Rightarrow {\text{ax}}^2+bx+c=0 \\ \iff \left[\begin{array}{l}{x}_1=\frac{{\displaystyle -b\text{'}+\sqrt{\Delta \text{'}}}}{{\displaystyle a}}\\ x_2=\frac{{\displaystyle -b\text{'}-\sqrt{\Delta \text{'}}}}{{\displaystyle a}}\end{array}\right. \\ \Delta \text{'}=0\Rightarrow {\text{ax}}^2+bx+c=0 \\ \iff x_1=x_2=\frac{{\displaystyle -b\text{'}}}{{\displaystyle a}} \\ \Delta \text{'}<0\Rightarrow {\text{\hspace{0.17em}ax}}^2+bx+c=0 \\ \iff x\in \varnothing \end{gathered}$$

- Xét phương trình ${\text{ax}}^2+bx+c=0$ ($a\ne 0$) có:

+) a + b + c = 0

$$\begin{gathered} {\text{⇔ax}}^2+bx+c=0 \\ \iff \left[\begin{array}{l}{x}_1=1\\ x_2=\frac{c}{a}\end{array}\right. \end{gathered}$$

+) a - b + c = 0

$$\begin{gathered} {\text{⇒ax}}^2+bx+c=0 \\ \iff \left[\begin{array}{l}{x}_1=-1\\ x_2=\frac{-c}{a}\end{array}\right. \end{gathered}$$

- Phương trình tích:

$A\left(x\right).B\left(x\right)=0\iff \left[\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}\right.$

- Phương trình chứa ẩn ở mẫu:

+ Tìm điều kiện xác định

+ Quy đồng mẫu số và bỏ mẫu số

+ Giải phương trình sau khi bỏ mẫu số

+ Kiểm tra nghiệm với điều kiện xác định xem có thỏa mãn hay không

+ Kết luận nghiệm

III. Ví dụ minh họa

Bài 1: Giải và biện luận các phương trình sau:

a) $2m{x}^2+5x-1=0$

b)$x^2-4x+2=0$

Lời giải:

a)

Khi $2m=0\iff m=0$, xét phương trình $2m{x}^2+5x-1=0$ trở thành phương trình bậc nhất 5x – 1 = 0 có duy nhất một nghiệm $x=\frac{1}{5}$

Khi $2m\ne 0\iff m\ne 0$, xét phương trình bậc hai:  $2m{x}^2+5x-1=0$

$\Delta =5^2-4.2m.(-1)=25+8m$

Với  $\Delta >0\iff 25+8m>0\iff m>\frac{-25}{8}$ và $m\ne 0$ thì phương trình bậc hai có hai nghiệm phân biệt: $x_1=\frac{-5+\sqrt{25+8m}}{4m}$,$x_2=\frac{-5-\sqrt{25+8m}}{4m}$

Với $\Delta =0\iff 25+8m=0\iff m=\frac{-25}{8}$ thì phương trình bậc hai có nghiệm kép:

$x_1=x_2=\frac{-b}{2a}=\frac{-5}{4m}=\frac{-5}{4.\left(\frac{-25}{8}\right)}=\frac{2}{5}$

Với $\Delta <0\iff 25+8m<0\iff m<\frac{-25}{8}$ thì phương trình bậc hai vô nghiệm.

b)

Xét phương trình bậc hai:$x^2-4x+2=0$

$$\begin{gathered} b\text{'}=\frac{b}{2}=\frac{-4}{2}=-2 \\ \Delta \text{'}={(-2)}^2-1.2=2 > 0 \end{gathered}$$

$\Rightarrow$ Phương trình có hai nghiệm phân biệt

$$\begin{gathered} x_1=\frac{-(-2)+\sqrt{2}}{1}=2+\sqrt{2} \\ {x}_2=\frac{-(-2)-\sqrt{2}}{1}=2-\sqrt{2} \end{gathered}$$

Bài 2: Giải phương trình:

$(x^2-3x+2)(2x^2+5x+3)=0$

Lời giải:

$(x^2-3x+2)(2x^2+5x+3)=0$ (1)

$\iff \left[\begin{array}{l}{x}^2-3x+2=0\\ 2x^2+5x+3=0\end{array}\right.$

Xét phương trình $x^2-3x+2=0$ có: 1 – 3 + 2 = 0

$\Rightarrow$Phương trình có hai nghiệm: $x_1=1$,$x_2=\frac{2}{1}=2$

Xét phương trình $2x^2+5x+3=0$ có: 2 – 5 + 3 = 0

$\Rightarrow$Phương trình có hai nghiệm: $x_3=-1$,$x_4=\frac{-3}{2}$

$\left(1\right)\iff \left[\begin{array}{l}x=1\\ x=-1\\ x=2\\ x=\frac{-3}{2}\end{array}\right.$

Vậy tập nghiệm của phương trình là $S=\left\{1;-1;2;\frac{-3}{2}\right\}$.

Bài 3: Giải phương trình: $\frac{2}{x-4}+\frac{4x}{x+1}=3$.

 Lời giải:

Điều kiện xác định của phương trình: $\left\{\begin{array}{l}x-4\ne 0\\ x+1\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne 4\\ x\ne -1\end{array}\right.$

Ta có:$\frac{2}{x-4}+\frac{4x}{x+1}=3$

$$\begin{gathered} \iff \frac{2(x+1)}{(x-4)(x+1)}+\frac{4x(x-4)}{(x+1)(x-4)} \\ =\frac{3(x+1)(x-4)}{(x+1)(x-4)} \\ \Rightarrow 2(x+1)+4x(x-4) \\ =3(x+1)(x-4) \\ \iff 2x+2+4x^2-16x \\ =3(x^2-4x+x-4) \\ \iff 2x+2+4x^2-16x \\ =3x^2-12x+3x-12 \\ \iff 2x+2+4x^2-16x-3x^2 \\ +12x-3x+12=0 \\ \iff x^2-5x+14=0 \end{gathered}$$

Xét phương trình  $x^2-5x+14=0$

$\Delta ={(-5)}^2-\mathrm{4.1.14}=-31<0$

$\Rightarrow$Phương trình $x^2-5x+14=0$ vô nghiệm

Vậy phương trình $\frac{2}{x-4}+\frac{4x}{x+1}=3$ vô nghiệm.

IV. Bài tập vận dụng 

Bài 1: Giải phương trình 3x² + 8x – 4 = 0.

Bài 2: Giải phương trình $\frac{3x}{2x-1}+\frac{x}{3}=4$.

Bài 3: Phương trình (m–1)x² + 3x – 1 = 0. Phương trình có nghiệm khi

Bài 4: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình mx² - mx + 1 = 0 có nghiệm.

Bài 5: Tìm tất cả các giá trị thực của tham số m để hai đồ thị hàm số y = -x² - 2x + 3 và y = x² - m có điểm chung

Bài 6: Tìm giá trị thực của tham số m để đường thẳng d: y = 2x + m tiếp xúc với parabol (P): y = (m–1)x² + 2mx + 3m – 1

Bài 7: Nếu m ≠ 0 và n ≠ 0 là các nghiệm của phương trình x² + mx + n = 0 thì tổng m + n bằng

Bài 8: Giả sử phương trình x² - 3x - m = 0 (m là tham số) có hai nghiệm là x₁, x₂. Tính giá trị biểu thức P = x₁²(1 - x₂) + x₂²(1 - x₁) theo m

Bài 9: Cho hai phương trình x² - 2mx + 1 = 0 và x²- 2x + m = 0. Có hai giá trị của m để phương trình này có một nghiệm là nghịch đảo của một nghiệm của phương trình kia. Tính tổng S của hai giá trị m đó

Bài 10: Cho phương trình x² + px + q = 0, trong đó p > 0, q > 0. Nếu hiệu các nghiệm của phương trình là 1. Thế thì p bằng

Bài 11: Nếu a, b, c, d là các số khác 0, biết c và d là nghiệm của phương trình x² + ax + b = 0 và a, b là nghiệm của phương trình x² + cx + d = 0. Thế thì a + b + c + d bằng

Bài 12: Biết rằng phương trình x² - 4x + m + 1 = 0 có một nghiệm bằng 3. Nghiệm còn lại của phương trình bằng

Bài 13: Có bao nhiêu giá trị của a để hai phương trình: x² + ax + 1 = 0 và x² – x – a = 0 có một nghiệm chung ?

Bài 14: Cho phương trình: x² – 2a(x – 1) – 1 = 0. Khi tổng các nghiệm và tổng bình phương các nghiệm của phương trình bằng nhau thì giá trị của tham số a bằng

Bài 15: Giả sử x₁ và x₂ là hai nghiệm của phương trình: x² + 3x – 10 = 0. Giá trị của tổng 1/x₁ + 1/x₂ là

Bài 16: Nếu biết các nghiệm của phương trình: x² + px + q = 0 là lập phương các nghiệm của phương trình x²+mx+n=0. 

Bài 17: Gọi x₁, x₂ là 2 nghiệm của phương trình 2x² – 4x – 1 = 0. Khi đó, giá trị của T = |x₁ - x₂| là

Bài 18: Gọi x₁, x₂ là các nghiệm của phương trình x² – 3x – 1 = 0. Ta có tổng x₁² + x₂² bằng

Bài 19: Gọi x₁, x₂ là hai nghiệm của phương trình x² - mx + m - 1 = 0 (m là tham số). Tìm giá trị nhỏ nhất P_min của biểu thức 

Bài 20: Gọi x₁, x₂ là hai nghiệm của phương trình x² - 2(m-1)x + 2m² - 3m + 1 = 0 (m là tham số). Tìm giá trị lớn nhất P_max của biểu thức P = |x₁ + x₂ + x₁x₂|

Bài 21: Gọi x₁, x₂ là hai nghiệm của phương trình 2x² + 2mx + m² - 2 = 0 (m là tham số). Tìm giá trị lớn nhất P_max của biểu thức P = |2x₁x₂ + x₁ + x₂ - 4|

V. Bài tập tự luyện 

Câu 1. Phương trình nào sau đây không thể quy về phương trình bậc hai?

A. $\sqrt{x^2-x+1}=\sqrt{x+3}$;          

B. $\sqrt{x+6}=2x-1$;                  

C. $\sqrt{x^2+2x-3}=\sqrt{2x^2+8x-7}$;                

D. $\sqrt{x^3-x^2+1}=3$.

Câu 2. Phương trình $\sqrt{4x^2-3}=x$ có nghiệm là:

A. x = 1;              

B. x = –1;            

C. x = 1 hoặc x = –1;              

D. Vô nghiệm.

Câu 3. Số nghiệm của phương trình $\sqrt{2x-4}=\sqrt{x^2-3x}$ là:

A. 0;          

B. 2;           

C. 3;           

D. 1.

Câu 4. Cho phương trình $\sqrt{3x^2-10x-44}-8+x=0$. Tổng các nghiệm của phương trình trên là:

A. 3;          

B. ‒6;                  

C. –3;                  

D. 0.

Câu 5. Cho phương trình $\sqrt{x^2+3}=\sqrt{2x+6}$. Khẳng định nào sau đây sai?

A. Tổng các nghiệm của phương trình đã cho là 2;                

B. Tích các nghiệm của phương trình đã cho là –5;                

C. Các nghiệm của phương trình đã cho đều lớn hơn –2;                 

D. Phương trình có hai nghiệm trái dấu.

Câu 6. Cho phương trình $2\sqrt{2x^2-3x+1}=\sqrt{9x^2+5x+4}$. Tổng các nghiệm của phương trình đã cho là:

A. –17;                

B. 5;           

C. 0;           

D. 17.

Câu 7. Cho phương trình $\sqrt{x^2+3}=\sqrt{2x+6}$. Chọn khẳng định đúng:

A. Phương trình có hai nghiệm phân biệt cùng dấu;               

B. Phương trình có hai nghiệm phân biệt trái dấu;                 

C. Phương trình có một nghiệm;                

D. Phương trình vô nghiệm.

Câu 8. Tập nghiệm của phương trình $\sqrt{\left(x-3\right)\left(2-x\right)}=\sqrt{4x^2+12x+9}$ là:

A. {10; 3};          

B. {5};                 

C. {3};                 

D. ∅.

Câu 9. Giá trị x nào sau đây là nghiệm của phương trình $\sqrt{2x^2+3x-5}=x+1$?

A. x = –3;            

B. x = 2;              

C. Cả A và B đều đúng;         

D. Cả A và B đều sai.

Câu 10. Số nghiệm của phương trình $\sqrt{-x^2+4x}=2x-2$ là:

A. 0;          

B. 1;           

C. 2;           

D. 3.

Câu 11. Số nghiệm của phương trình $\sqrt{-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}}+x=1$ là:

A. 0;          

B. 2;           

C. 1;           

D. 3.

Câu 12. Phương trình $\sqrt{x-2}-3\sqrt{x^2-4}=0$ có nghiệm là:

A. x = 2;              

B. $x=-\frac{17}{9}$;         

C. Cả A và B đều đúng;         

D. Cả A và B đều sai.

Câu 13. Cho phương trình $x+\sqrt{5+2x^2}=6$. Khẳng định nào sau đây đúng?

A. Phương trình có một nghiệm;                

B. Phương trình vô nghiệm;             

C. Tổng các nghiệm của phương trình là –12;              

D. Các nghiệm của phương trình đều không nhỏ hơn –10.

Câu 14. Cho phương trình $\frac{\sqrt{x^2-3x-4}}{x+1}=-2$. Biết phương trình đã cho có một nghiệm có dạng $\frac{a}{b}$, với $\frac{a}{b}$ là phân số tối giản và b > 0. Khi đó giá trị biểu thức a² – b² bằng:

A. 55;                  

B. 0;           

C. $\frac{55}{2}$;                 

D. –55.

Câu 15. Giao điểm của hai đồ thị hàm số $y=4\sqrt{2x^2-3x+1}$ và $y=\sqrt{9x^2+54x+81}$ là:

A. A(5; 24);                  

B. $B\left(-\frac{13}{23};\frac{168}{23}\right)$;          

C. Cả A, B đều đúng;             

D. Cả A, B đều sai.

Câu 16. Cho phương trình:

$\sqrt{x^2+x+10-2\sqrt{x^2+x+7}}=\sqrt{x^2+x+15-6\sqrt{x^2+x+7}}$.

Tập nghiệm của phương trình trên là:

A. $\left\{\frac{-2-\sqrt{91}}{4}\right\}$;

B. $\left\{\frac{-2+\sqrt{91}}{4};\frac{-2-\sqrt{91}}{4}\right\}$        

C. $\left\{\frac{-2+\sqrt{91}}{4}\right\}$;             

D. ∅.

Câu 17. Số giao điểm giữa đồ thị hàm số $y=\sqrt{3x-4}$ và đồ thị hàm số y = x – 3 là:

A. 2 giao điểm;             

B. 4 giao điểm;              

C. 3 giao điểm;              

D. 1 giao điểm.

Câu 18. Tổng bình phương các nghiệm của phương trình $\left(x-2\right)\sqrt{2x+7}=x^2-4$ bằng:

A. 10;                  

B. 5;           

C. 13;                  

D. 14.

Câu 19. Cho ∆MNP vuông tại M có MN dài hơn MP 10 cm. Biết chu vi của ∆MNP là 50 cm. Độ dài của cạnh NP bằng khoảng:

A. 21,41 cm;                 

B. 11,5 cm;          

C. 28,71 cm;                 

D. 32,21 cm.

Câu 20. Khoảng cách từ nhà An ở vị trí A đến nhà Bình là 200 m. Từ nhà, nếu An đi x mét theo phương tạo với AB một góc 120° thì sẽ đến nhà bác Mai ở vị trí M và nếu đi thêm 300 m nữa thì sẽ đến siêu thị ở vị trí S.

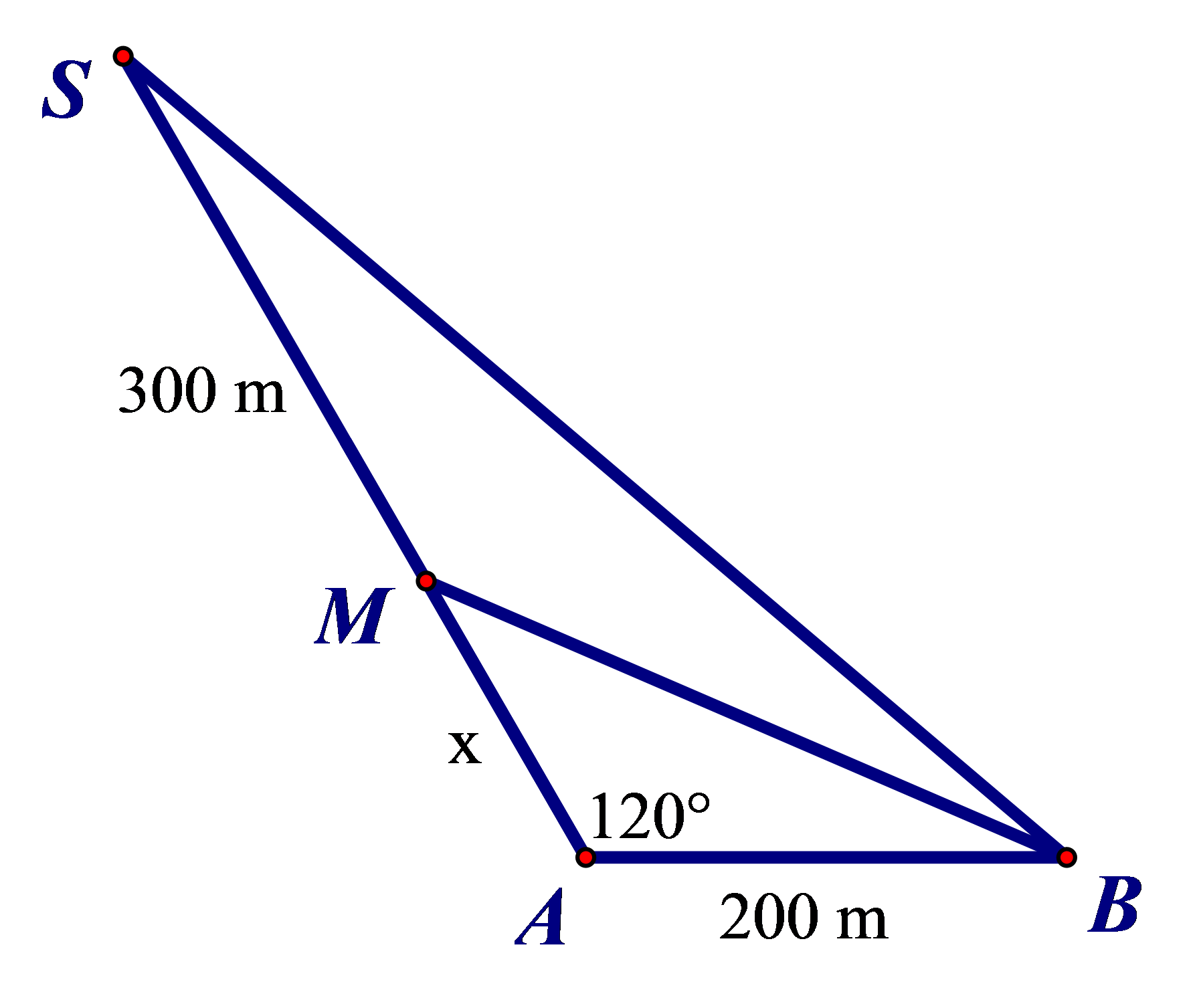
Biết rằng quãng đường từ nhà Bình đến siêu thị gấp đôi quãng đường từ nhà Bình đến nhà bác Mai. Khi đó quãng đường từ nhà An đến nhà bác Mai là:

A. 50 m;              

B. 75 m;              

C. 100 m;            

D. 200 m.

Xem các phương pháp giải bài tập hay, chi tiết khác:

Tất tần tật về Hệ thức Vi-et | Công thức Hệ thức Vi-et

Công thức giải phương trình chứa dấu giá trị tuyệt đối chi tiết

Công thức giải phương trình chứa dấu căn chi tiết

Công thức giải hệ phương trình bậc nhất hai ẩn, ba ẩn chi tiết

Bất đẳng thức lớp 10 và cách giải bài tập