Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bất đẳng thức chứa dấu giá trị tuyệt đối (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Bất đẳng thức chứa dấu giá trị tuyệt đối (HAY NHẤT 2024)
I. Lí thuyết tổng hợp
Từ định nghĩa giá trị tuyệt đối, ta có các tính chất như sau:
Với mọi số thực x có: ,
Với mọi số thực x và số thực a > 0 có:
hoặc
Với mọi số thực a, b có:
II. Các công thức
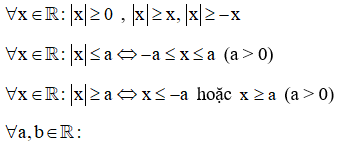
(Dấu bằng xảy ra khi và )
(Dấu bằng xảy ra khi )
III. Ví dụ minh họa
Bài 1: Chứng minh rằng với mọi số thực x.
Lời giải:
Ta có:
Mặt khác:
(điều cần phải chứng minh)
Bài 2: Chứng minh rằng: với mọi số thực a, b, c.
Lời giải:
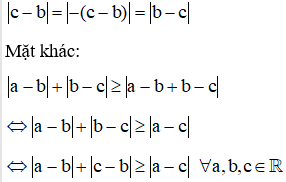
(điều cần phải chứng minh).
Bài 3: Chứng minh rằng với mọi số thực x.
Lời giải:
Ta có:
(điều cần phải chứng minh).
IV. Bài tập vận dụng
Bài 1: Chứng minh rằng: với mọi số thực a, b, c.
Bài 2: Cho . Chứng minh rằng .
Bài 3: Chứng minh rằng 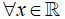
Bài 4: Tìm tất cả các số nguyên x để biểu thức sau đây đạt giá trị nhỏ nhất:
Bài 5: Giải các bất phương trình: |2x – 5| ≤ x + 3
Bài 6: a) Chứng minh rằng với mọi số thực a, b ta có |a ± b| ≥ |a| - |b|.
b) Biết rằng | a | > 2 | b |. Chứng minh rằng |a| < 2|a - b|.
Bài 7: Chứng minh rằng: a. Nếu x ≥ y ≥ 0 thì 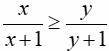
b. Với hai số a, b tuỳ ý, ta có
Bài 8: Giải các phương trình:
a)
b)
c)
d)
Bài 9: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) trong hai trường hợp và
b) trong hai trường hợp và
c) khi
d)
Bài 10: Giải các phương trình:
a)
b)
c)
d)
Bài 11: Cho chứng minh:
a)
b)
c)
d)
Bài 12: Kiểm tra xem -2 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a)
b)
c)
d)
e)
f)
Bài 13: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a)
b)
c)
d)
Bài 14: Giải các bất phương trình:
a)
b)
c)
d)
Bài 15: Giải các bất phương trình:
a)
b)
c)
d)
Bài 16: Tìm x sao cho:
a) Giá trị của biểu thức là số dương
b) Giá trị của biểu thức nhỏ hơn giá trị của biểu thức
c) Giá trị của biểu thức không nhỏ hơn giá trị của biểu thức
d) Giá trị của biểu thức không lớn hơn giá trị của biểu thức
Bài 17: Trong một cuộc thi đố vui. Ban tổ chức quy định mỗi người dự thi phải trả lời 10 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn 4 đáp án, nhưng trong đó chỉ có 1 đáp án đúng. Người dự thi chọn đáp án đúng sẽ được 5 điểm, chọn đáp án sai sẽ bị trừ đi 1 điểm. Ở vòng sơ tuyển, Ban tổ chức tặng cho mỗi người dự thi 10 điểm và quy định người nào có tổng số điểm từ 40 trở lên mới được dự thi ở vòng tiếp theo. Hỏi người dự thi phải trả lời chính xác bao nhiêu câu hỏi ở vong sơ tuyển thì mới được dự thi tiếp ở vòng sau?
Bài 18: Giải các phương trình:
a)
b)
c)
d)
V. Bài tập tự luyện
Bài 1: Biểu thức A = | 4x | + 2x - 1 với x < 0, rút gọn được kết quả là?
A. A = 6x - 1
B. A = 1 - 2x
C. A = - 1 - 2x
D. A = 1 - 6x
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | + 2x - 1 = - 4x + 2x - 1 = - 2x - 1
Chọn đáp án C.
Bài 2: Tập nghiệm của phương trình: | 3x + 1 | = 5
A. S = { - 2 }
B. S = { }
C. S = { - 2; }
D. S = { Ø }
Ta có: | 3x + 1 | = 5 ⇔
Vậy tập nghiệm của phương trình đã cho là S = { - 2; }
Chọn đáp án C.
Bài 3: Tập nghiệm của phương trình |2 - 3x| = |5 - 2x| là?
A. S = { - 3;1 }
B. S = { - 3; }
C. S = { 0; }
D. S = { - 3;1 }
Ta có: |2 - 3x| = |5 - 2x| ⇔
Vậy tập nghiệm của phương trình là S = { - 3; }
Chọn đáp án B.
Bài 4: Giá trị m để phương trình | 3 + x | = m có nghiệm x = - 1 là?
A. m = 2
B. m = - 2
C. m = 1
D. m = - 1
Phương trình đã cho có nghiệm x = - 1 nên ta có: | 3 + ( - 1 ) | = m ⇔ m = 2.
Vậy m = 2 là giá trị cần tìm.
Chọn đáp án A.
Bài 5: Giá trị của m để phương trình | x - m | = 2 có nghiệm là x = 1 ?
A. m ∈ { 1 }
B. m ∈ { - 1;3 }
C. m ∈ { - 1;0 }
D. m ∈ { 1;2 }
Phương trình có nghiệm x = 1, khi đó ta có:
| 1 - m | = 2 ⇔
Vậy giá trị m cần tìm là m ∈ { - 1;3 }
Chọn đáp án B.
Bài 6: Rút gọn biểu thức A = |2x + 4| + 2(x - 3) với x > 0
A. 4x - 2 B. 3 – 4x C. -10 D. 4x -10
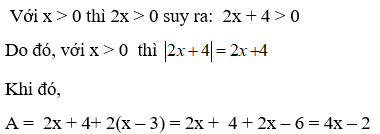
Chọn đáp án A
Bài 7: Với x > 2 thì |3 - (2x - 1)| bằng ?
A. 2x + 4 B. 2x - 4 C. 2x - 1 D. 2x – 2
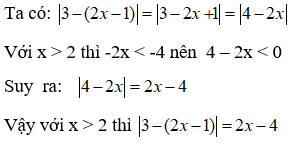
Bài 8: Tìm tất cả các giá trị của x thỏa mãn: |6 - 2(x + 2)| = 2 - 2x
A. x = 1 B. x < 1 C. x ≤ 1 D. x > 1
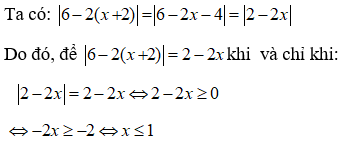
Chọn đáp án C
Bài 9: Giải phương trình sau: |x + 1| = 2x + 7
A. x = 8 hoặc x = -2
B. x = 2
C. x = 2 hoặc x = 8
D. x = 8
Lời giải:
Ta có: |x + 1| = x + 1 nếu x ≥ -1 Và |x + 1| = -x - 1 nếu x < -1
Để giải phương trình đã cho ta quy về giải hai phương trình sau:
* Phương trình x + 1 = 2x -7 với ⇔ -x = - 7 -1 ⇔ - x = -8 ⇔ x = 8 (thỏa mãn điều kiện )
* Phương trình –x – 1= 2x – 7 với x < -1
⇔ -x - 2x = -7 + 1
⇔ - 3x = - 6
⇔ x = 2 ( không thỏa mãn điều kiện x < -1)
Vậy nghiệm của phương trình đã cho là x = 8
Bài 10: Giải phương trình |2 - (x + 4)| = |2x - 3(x + 2)|
A. x = 3 hoặc x = -4
B. x = 1 hoặc x = -2
C. x = -4
D. x = 4 và x = 2
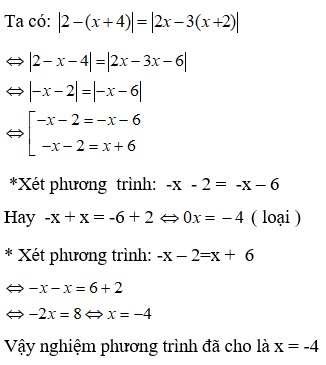
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Dấu của nhị thức bậc nhất chi tiết nhất
Công thức giải bất phương trình một ẩn chi tiết nhất
Công thức giải bất phương trình chứa dấu giá trị tuyệt đối chi tiết nhất
Dấu của tam thức bậc hai chi tiết nhất
Công thức giải bất phương trình bậc hai một ẩn chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.