Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Dấu của tam thức bậc hai (50 bài tập minh họa) HAY NHẤT 2024 hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 10.
Nội dung bài viết
Phương pháp giải Dấu của tam thức bậc hai (50 bài tập minh họa) HAY NHẤT 2024
I. Lí thuyết tổng hợp
- Tam thức bậc hai đối với x là biểu thức có dạng f(x)=ax2+bx+c, trong đó a, b, c gọi là các hệ số và a≠0.
- Dấu của tam thức bậc hai: Cho f(x)=ax2+bx+c (a≠0), Δ=b2−4ac (biệt thức của tam thức bậc hai), ta có:
+ Nếu Δ< 0 thì f(x) luôn cùng dấu với hệ số a với mọi số thực x
+ Nếu Δ= 0 thì f(x) luôn cùng dấu với hệ số a và bằng 0 khi
+ Nếu Δ> 0 thì f(x) luôn cùng dấu với hệ số a khi x<x1 hoặc x>x2, trái dấu với hệ số a khi x1<x<x2, trong đó x1,x2(x1<x2) là hai nghiệm của phương trình f(x) = 0.
- Chú ý: Có thể thay Δ=b2−4ac bằng Δ'=b'2−ac với b'=b2
II. Các công thức
Cho f(x)=ax2+bx+c (a≠0), Δ=b2−4ac (Δ'=b'2−ac với b'=b2)
+) Nếu Δ< 0 thì với ∀x∈ℝ
a>0⇒f(x)>0a<0⇒f(x)<0
+) Nếu Δ thì
a<0⇒f(x)<0∀x∈ℝ\{−b2a}a>0⇒f(x)>0∀x∈ℝ\{−b2a}x=−b2a⇔f(x)=0
+) Nếu Δ và f(x)=0⇔[x=x1x=x2 (x1<x2) thì
a<0⇒{f(x)<0∀x∈(−∞;x1)∪(x2;+∞)f(x)>0∀x∈(x1;x2)a>0⇒{f(x)>0∀x∈(−∞;x1)∪(x2;+∞)f(x)<0∀x∈(x1;x2)
III. Ví dụ minh họa
Bài 1: Xét dấu tam thức bậc hai: 5x2−3x+1.
Lời giải:
Xét f(x) = 5x2−3x+1
Ta có: Δ=(−3)2−4.5.1=−11<0
Và hệ số a = 5 > 0 nên ta có: f(x) = 5x2−3x+1 > 0 ∀x∈ℝ.
Bài 2: Xét dấu tam thức bậc hai: x2−4x−5.
Lời giải:
Xét f(x) = x2−4x−5
Ta có: Δ'=(−2)2−1.(−5)=9>0
Nghiệm của f(x) = 0 là:
x1=−(−2)+√91=5 ,
x2=−(−2)−√91=−1
Có hệ số a = 1 > 0 nên ta có:
f(x) = x2−4x−5 > 0 khi x∈(−∞;−1)∪(5;+∞)
f(x) = x2−4x−5< 0 khi x∈(−1;5).
Bài 3: Xét dấu tam thức bậc hai: x2−2x+1.
Lời giải:
Xét f(x) = x2−2x+1
Ta có: Δ=(−2)2−4.1.1=0
Và hệ số a = 1 > 0 nên ta có: Nghiệm x0=−b2a=−(−2)2.1=1
f(x) = x2−2x+1 > 0 khi x∈ℝ\{1}
f(x) = x2−2x+1 = 0 khi x = 1
IV. Bài tập vận dụng
Bài 1: Xét dấu tam thức bậc hai: −3x2+4x−6.
Bài 2: Xét dấu tam thức bậc hai: −4x2+5x+8.
Bài 3: Hãy xét dấu của 3 tam thức bậc hai sau
f (x) = x2−5x + 6
g (x) = – x2 + 4x + 5
h (x) = 6x2 + x + 4
Bài 4: Xét dấu tam thức bậc 2 của các biểu thức sau:
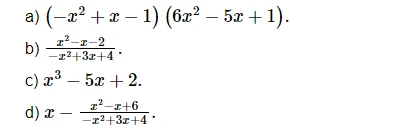
Bài 5: Vận dụng kiến thức đã học để tìm m. Sao cho phương trình có nghiệm
a) (x2 + 2x)2 – 4m(x2 + 2x) + 3m + 1 = 0
b) x4 + mx3 + 2mx2 +mx +1 =0
Bài 6: Tìm m sao cho f(x) = m(x2 – 2)x2 -2(m+3)x – m +3 > 0 với ∀ x ∈ ( −∞; 1).
Bài 7: Chứng minh rằng phương trình f(x) = m(x2 -9) + x(x-5) = 0 luôn có nghiệm.
Bài 8: So sánh 5 với nghiệm của phương trình 2x2 – 12x + 9 =0
Bài 9: So sánh -8 với nghiệm của phương trình 9x2 + 3x – (m+2) = 0
V. Bài tập tự luyện
Bài 1: Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 2x + 1 là:
A. 
B. 
C. 
D.
Bài 2: Biểu thức nào sau đây là tam thức bậc hai
A. f(x) = x + 2;
B. f(x) = 2x3 + 2x2 – 1;
C. f(x) = x2 – 3x;
D. f(x) = 2x – 1.
Bài 3: Với x thuộc tập hợp nào dưới đây thì đa thức f(x) = x2 – 6x + 8 không dương?
A. [2; 3];
B. (−∞;2)∪(4;+∞);
C. [2; 4];
D. [1; 4].
Bài 4: Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m + 3 luôn dương là
A. m < 1;
B. m ≥ 1;
C. m > 1;
D. m ∈ ∅.
Bài 5: Tam thức nào sau đây nhận giá trị âm với mọi x < 1
A. f(x) = x2 – 5x +6 ;
B. f(x) = x2 – 16;
C. f(x) = x2 + 2x + 3;
D. f(x) = – x2 + 5x – 4.
Bài 6: Cho hàm số f(x) = mx2 – 2mx + m – 1. Giá trị của m để f(x) < 0 ∀x ∈ ℝ.
A. m ≥ 0;
B. m > 0;
C. m < 0;
D. m ≤ 0.
Bài 7: Tìmtất cả các giá trị thực của tham số m để f(x) = (m – 3)x2 + (m + 2)x – 4 nhận giá trị không dương với mọi giá trị của x.
A. (m≤−22m≥2);
B. – 22 ≤ m ≤ 2;
C. – 22 < m < 2;
D. (−22≤m≤2m=3).
Bài 8: Tìm tất cả các giá trị của m để tam thức f(x) = mx2 – x + m luôn dương với ∀x ∈ ℝ
A.m > 0;
B. m < 0;
C.m>12;
D.m<12.
Bài 9: Tam thức y = – x2 – 3x – 4 nhận giá trị âm khi và chỉ khi
A. x < 4 hoặc x > – 1;
B. x < 1 hoặc x > 4;
C. – 4 < x < 4;
D. x ∈ ℝ.
Bài 10: Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
A. m < – 1;
B. m < 0;
C. – 1 < m < 0;
D. m < 1 và m ≠ 0.
Bài 11: Xác định m để biểu thức f(x) = (m + 2)x2 – 3mx + 1 là tam thức bậc hai
A. m = 2;
B. m = – 2;
C. m ≠ 2;
D. m ≠ – 2.
Bài 12: Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi
A. m ≤ - 4 hoặc m ≥ 0;
B. m < - 4 hoặc m > 0;
C. – 4 < m < 0;
D. m < 0 hoặc m > 4.
Bài 13: Các giá trị m để tam thức f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu 2 lần là
A. m ≤ 0 hoặc m ≥ 28;
B. m < 0 hoặc m > 28;
C. 0 < m < 28;
D. m > 0.
Bài 14: Cho tam thức f(x) = x2 + 2mx + 3m – 2. Tìm m để f(x) ≥ 0 với mọi x ∈ ℝ.
A. 1 ≤ m ≤ 2;
B. 1 < m < 2;
C. m < 1;
D. m > 2.
Bài 15: Cho tam thức bậc hai f(x) = ax2 + bx + c có đồ thị như hình vẽ dưới đây
Bảng biến thiên của tam thức bậc hai là
A.
B.
C.
D.
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Bất đẳng thức chứa dấu giá trị tuyệt đối chi tiết nhất
Dấu của nhị thức bậc nhất chi tiết nhất
Công thức giải bất phương trình một ẩn chi tiết nhất
Công thức giải bất phương trình chứa dấu giá trị tuyệt đối chi tiết nhất
Công thức giải bất phương trình bậc hai một ẩn chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.