Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Tất tần tật về Định lí Côsin và hệ quả (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Tất tần tật về Định lí Côsin và hệ quả (HAY NHẤT 2024)
I. Lí thuyết tổng hợp
- Định lí Côsin:
Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.
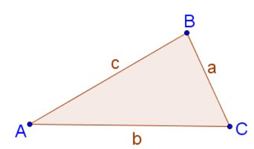
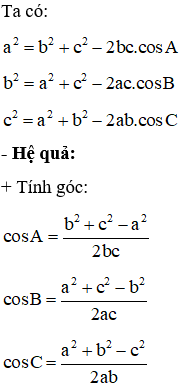
+ Tính diện tích:
. ( là độ dài đường cao lần lượt kẻ từ đỉnh A, B, C)
(với R là bán kính đường tròn ngoại tiếp)
S = pr (với r là bán kính đường tròn nội tiếp, )
(với ) (công thức Hê – rông)
II. Các công thức cần nhớ
Cho tam giác ABC bất kì có diện tích S với AB = c, AC = b, BC = a. Ta có:
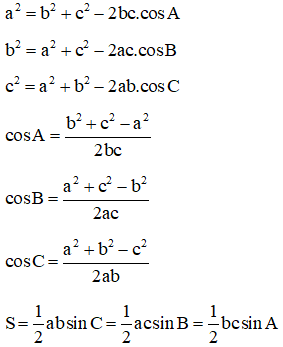
(với R là bán kính đường tròn ngoại tiếp)
S = pr (với r là bán kính đường tròn nội tiếp, )
(với ) (công thức Hê – rông)
III. Ví dụ minh họa
Câu 1: Cho tam giác ABC có AB = 4, AC = 6, góc A = 120o. Độ dài cạnh BC là:A. √19 B. 2√19 C. 3√19 D. 2√7
Câu 2: Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Giá trị cos A bằng
A. 0,125 B. 0,25 C. 0,5 D. 0,0125
Câu 3: Cho tam giác ABC có a = 3, b = 5, c = 6. Giá trị của mc bằng
A. √2 B. 2√2 C. 3 D. √10
Câu 4: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
Câu 5: Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
Câu 6: Cho tam giác ABC có AB = 10, AC = 12, góc A = 150o.Diện tích của tam giác ABC bằng
A. 60 B. 30 C.60√3 D. 30√3
Câu 7: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng
A. 4 B. 3 C. 2 D. 1
Câu 8: Cho tam giác ABC có AC = 6, BC = 8. ha ,hb lần lượt là độ dài các đường cao đi qua các đỉnh A, B. Tỉ số ha/hb bằng
Câu 9: Cho tam giác ABC có a = 5, b = 6, c = 7. Diện tích của tam giác ABC bằng
A. 12√6 B. 3√6 C. 6√6 D. 9√6
Câu 10: Cho tam giác ABC có a = 3, b = 5, c = 6. Bán kính đường trong nội tiếp của tam giác bằng
Câu 11: Cho tam giác ABC có a = 5, b = 12, c = 13. Bán kính đường tròn ngoại tiếp R của tam giác bằng
A. 13 B. 26 C. 6,5 D. 7,5
Câu 12: Cho tam giác ABC có a = 2, b=2√2 ,góc C = 135o. Độ dài cạnh c là
A. 8 B. 4√2 C. 2√2 D. 2√5
Câu 13: Cho tam giác ABC có a=√3,b=4,c=2√3. Giá trị của cos B là:
Câu 14: Cho tam giác ABC có a = 2, b = 3, c=√19. Số đo của góc C là
A. 135o B. 150o C. 60o D. 120o
Câu 15: Cho tam giác ABC có a2 =b2 + c2 - bc. Số đo của góc A là
A. 135o B. 150o C. 60o D. 120o
Câu 16: Cho tam giác ABC có a2 =b2 + c2 + √2.bc. Số đo của góc A là
A. 135o B. 45o C. 120o D. 150o
Câu 17: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A. Nếu b2 +c2 > a2 thì góc A > 90o
B. Nếu b2 +c2 = a2 thì góc A ≠ 90o
C. Nếu b2 +c2 ≠ a2 thì tam giác ABC không phải là tam giác vuông
D. Nếu b2 +c2 > a2 thì góc A > 90
Câu 18: Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Câu 19: Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Câu 20: Cho tam giác ABC có a = 6 cm, b = 7 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Câu 21: Cho tam giác ABC. Biểu thức P = ab.cos C + bc.cos A +ca. cosB bằng
Câu 22: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
Câu 23: Cho tam giác ABC, có a=√31 ,b= √29 ,c= 2√7 . Giá trị của mc là
A. 2√23 B. √23 C. √23/2 D. 5
Câu 24: Cho tam giác ABC có a = 4, b = 6, mc=4. Giá trị của c là
A. 2√10 B. √10 C. 3√10 D. √10/2
Câu 25: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
Câu 26: Cho tam giác ABC trọng tâm G. Bình phương độ dài đoạn thẳng GA bằng
Câu 27: Cho tam giác ABC thỏa mãn c = a.cos B. Khẳng định nào sau đây là đúng?
A. Tam giác ABC là tam giác cân
B. Tam giác ABC là tam giác nhọn
C. Tam giác ABC là tam giác vuông
D. Tam giác ABC là tam giác tù
Câu 28: Cho tam giác ABC có a = 30, góc = 60o. Khẳng định nào sau đây là đúng?
A. R = 10√3 B. R = 20√3 C. R = 10 D. R = 20
Câu 29: Cho tam giác ABC có a = 10 cm, ha = 3 cm. Diện tích của tam giác ABC là
A. 30 (cm)2 B. 15 (cm)2 C. 60 (cm)2 D. 7,5 (cm)2
Câu 30: Cho tam giác ABC có AB = 4, AC =6, BC = 8. Diện tích của tam giác ABC là
A. 3√15 B. 6√15 C. (3√15)/2 D. √15
Câu 31: Cho tam giác ABC có AB = 4, AC = 6, góc A = 30o. Diện tích của tam giác ABC là
A. 12 B. 6 C. 6√3 D. 6√2
Câu 32: Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Bán kính đường tròn nội tiếp của tam giác bằng
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
Câu 33: Cho tam giác ABC có a = 7, b = 8, c = 9. Bán kính đường tròn nội tiếp tam giác bằng
A. √7 B. √3 C. √5 D. 3
Câu 34: Cho tam giác ABC có a = 5, b = 7, c = 8. Bán kính đường tròn ngoại tiếp tam giác bằng
Câu 35: Đáp án nào sau đây phù hợp với diện tích của hình lục giác ở hình bên?
A. 12 + 8√3
B. 24 + 16√3
C. 24 + 4√3
D. 24 + 8√3
Câu 36: Bề mặt viên gạch hình lục lăng có dạng hình lục giác đều cạnh 8 cm. Diện tích bề mặt của viên gạch là
A. 96 (cm)2 C. 96√3 (cm)2
B. 16√3 (cm)2 D. 48√3 (cm)2
Câu 37: Tam giác cân cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là
A. a2cosα/2
B. a2sinα/2
C. a2cosα
D. a2sinα
Câu 38: Đa giác đều n đỉnh và nội tiếp đường tròn bán kính R có diện tích là
Câu 39: Đáp án nào sau đây phù hợp với diện tích của phần được tô ở hình bên?
A. 48 (cm)2
B. 32 (cm)2
C. 40 (cm)2
D. 56 (cm)2
Câu 40: Đáp án nào sau đây phù hợp với diện tích của tam giác ABC trong hình bên?
A. 13/2 B. (13√3)/2 C. 13 D. 13√3
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Công thức tính độ dài đường trung tuyến chi tiết nhất
Tất tần tật về Định lí Sin chi tiết nhất
Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.