Các công thức tính diện tích tam giác (50 bài tập minh họa) HAY NHẤT 2024

Ngọc Nguyễn Ngày: 21-08-2023 Lớp 10

162

Toptailieu.vn biên soạn và giới thiệu Các công thức tính diện tích tam giác (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Các công thức tính diện tích tam giác (50 bài tập minh họa) HAY NHẤT 2024

I. Các công thức

Cho tam giác có BC = a, AC = b, AB = c với:

• $h_{a}, h_{b}, h_{c}$ là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB

• R là bán kính đường tròn ngoại tiếp tam giác;

• r là bán kính đường tròn nội tiếp tam giác;

• $p = \frac{a + b + c}{2}$ là nửa chu vi tam giác;

• S là diện tích tam giác.

Khi đó ta có các công thức tính diện tích tam giác ABC như sau:

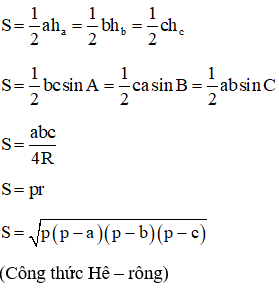
Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 (ảnh 1)

+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.

II. Ví dụ minh họa

Bài 1. Cho tam giác ABC có AB = 3, AC = 6, $\hat{B A C} = 60 °$ . Tính diện tích tam giác ABC.

Lời giải:

Diện tích tam giác ABC là:

$S = \frac{1}{2} A B . A C . \sin B A C$

$= \frac{1}{2} .3.6. \sin 60 ° = \frac{9 \sqrt{3}}{2}$ (đvdt).

Bài 2. Tam giác ABC có AC = 4, $\hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

Lời giải:

Theo định lý tổng 3 góc trong tam giác ABC, ta có:

Các công thức tính diện tích tam giác đầy đủ, chi tiết nhất - Toán lớp 10 (ảnh 1)

Bài 3. Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:

Lời giải:

Nửa chu vi tam giác ABC là:

$p = \frac{a + b + c}{2} = \frac{21 + 17 + 10}{2} = 24$ (đvđd)

Theo công thức Hê – rông, ta có diện tích tam giác ABC là:

$S = \sqrt{p (p - a) (p - b) (p - c)}$

$= \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$ (đvdt).

Bài 4. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng bao nhiêu?

Lời giải:

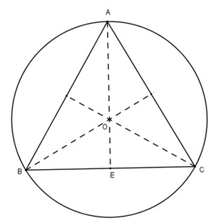
Giả sử tam giác thỏa mãn yêu cầu đề bài là tam giác ABC đều có cạnh a (cm, a > 0).

Theo đề bài ta có, đường tròn có bán kính R = 4 cm là đường tròn ngoại tiếp tam giác ABC, khi đó tâm O của đường tròn chính là giao của ba đường trung trực của tam giác.

Mà tam giác ABC đều nên O đồng thời là trực tâm của tam giác.

Gọi E là trung điểm của BC

Khi đó ta có: $A E = \frac{3}{2} A O$ (tính chất trọng tâm)

Mà AO = R = 4 cm

Do đó: AE = 6 cm

Tam giác ABC đều nên trung tuyến AE cũng là đường cao.

Theo định lý Py – ta – go trong tam giác vuông ABE ta có:

$A B^{2} = A E^{2} + B E^{2}$

Suy ra: $a^{2} = 6^{2} + {(\frac{a}{2})}^{2} \Rightarrow a = 4 \sqrt{3} (c m)$

Vậy diện tích tam giác đều ABC là:

$S = \frac{A B . A C . B C}{4 R} = \frac{{(4 \sqrt{3})}^{3}}{4.4} = 12 \sqrt{3}$ (cm²).

III. Bài tập tự luyện

Câu 1. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$ .

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$ .

C. $S_{Δ A B C} = 9$ .

D. $S_{Δ A B C} = \frac{9}{2}$ .

Câu 2. Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 8$ .

B. $S_{Δ A B C} = 4 \sqrt{3}$ .

C. $S_{Δ A B C} = 4$ .

D. $S_{Δ A B C} = 8 \sqrt{3}$ .

Câu 3. Tam giác ABC có $a = 21, b = 17, c = 10$ . Diện tích của tam giác ABC bằng:

A. $S_{Δ A B C} = 16$ .

B. $S_{Δ A B C} = 48$ .

C. $S_{Δ A B C} = 24$ .

D. $S_{Δ A B C} = 84$ .

Câu 4. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao $h_{a}$ của tam giác.

A. $h_{a} = 3 \sqrt{3}$ .

B. $h_{a} = \sqrt{3}$ .

C. $h_{a} = 3$ .

D. $h_{a} = \frac{3}{2}$ .

Câu 5. Tam giác $A B C$ có $A C = 4, \hat{A C B} = 60 °$ . Tính độ dài đường cao H xuất phát từ đỉnh A của tam giác.

A. $h = 2 \sqrt{3}$ .

B. $h = 4 \sqrt{3}$ .

C. $h = 2$ .

D. $h = 4$ .

Câu 6. Tam giác ABC có $a = 21, b = 17, c = 10$ . Gọi $B'$ là hình chiếu vuông góc của $B$ trên cạnh $A C$ . Tính $B B'$ .

A. $B B' = 8$ .

B. $B B' = \frac{84}{5}$ .

C. $B B' = \frac{168}{17}$ .

D. $B B' = \frac{84}{17}$ .

Câu 7. Tam giác $A B C$ có $A B = 8$ cm, $A C = 18$ cm và có diện tích bằng 64 ${cm}^{2}$ . Giá trị $\sin A$ bằng:

A. $\sin A = \frac{\sqrt{3}}{2}$ .

B. $\sin A = \frac{3}{8}$

C. $\sin A = \frac{4}{5}$ .

D. $\sin A = \frac{8}{9}$ .

Câu 8. Hình bình hành $A B C D$ có $A B = a, B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

A. $2 a^{2}$ .

B. $a^{2} \sqrt{2}$ .

C. $a^{2}$ .

D. $a^{2} \sqrt{3}$ .

Câu 9. Tam giác ABC có . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$ ;

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$ ;

C. $S_{Δ A B C} = 9$ ;

D. $S_{Δ A B C} = \frac{9}{2}$ .

Câu 10. Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 8$ ;

B. $S_{Δ A B C} = 4 \sqrt{3}$ ;

C. $S_{Δ A B C} = 4$ ;

D. $S_{Δ A B C} = 8 \sqrt{3}$ .

Câu 11. Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao hkẻ từ đỉnh A xuống cạnh BC của tam giác.

A. $h = 3 \sqrt{3}$ ;

B. $h = \sqrt{3}$ ;

C. $h = 3$ ;

D. $h = \frac{3}{2}$ ;

Câu 12. Tam giác ABC có $A C = 4, \hat{A C B} = 60 °$ . Tính độ dài đường cao hxuất phát từ đỉnh A của tam giác.

h = 2 \sqrt{3}

;

B. $h = 4 \sqrt{3};$

C. $h = 2;$

D. $h = 4.$

Câu 13. Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.

A. BB’ = 8;

B. $B B' = \frac{84}{5}$ ;

C. $B B' = \frac{168}{17}$ ;

D. $B B' = \frac{84}{17}$ .

Câu 14. Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng 64 ${cm}^{2}$ . Giá trị sinAbằng:

A. $\sin A = \frac{\sqrt{3}}{2}$ ;

B. $\sin A = \frac{3}{8}$ ;

C. $\sin A = \frac{4}{5}$ ;

D. $\sin A = \frac{8}{9}$ .

Câu 15. Hình bình hành ABCD có $A B = a, B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

A. $2 a^{2}$ ;

B. $a^{2} \sqrt{2}$ ;

C. $a^{2}$ ;

D. $a^{2} \sqrt{3}$ .

Câu 16. Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:

A. ${50 cm}^{2}$ ;

B. $50 \sqrt{2} {cm}^{2};$

C. ${75 cm}^{2}$ ;

D. $15 \sqrt{105} {cm}^{2}$ .

Câu 17. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:

A. $13 {cm}^{2}$ ;

B. $13 \sqrt{2} {cm}^{2}$ ;

C. $12 \sqrt{3} {cm}^{2};$

D. $15 {cm}^{2}$ .

Câu 18. Tam giác ABC có $B C = 2 \sqrt{3}, A C = 2 A B$ và độ dài đường cao AH = 2. Tính độ dài cạnh AB.

A. AB = 2;

B. $A B = \frac{2 \sqrt{3}}{3}$ ;

C. AB = 2 hoặc $A B = \frac{2 \sqrt{21}}{3}$ ;

D. AB = 2 hoặc $A B = \frac{2 \sqrt{3}}{3}$ .

Câu 19. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S;

B. 3S;

C. 4S;

D. 6S.

Câu 20. Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. $60^{0}$ ;

B. $90^{0}$ ;

C. $150^{0}$ ;

D. $120^{0}$ .

Câu 21.Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là

A. $\frac{a^{2} \cos α}{2}$ ;

B. $\frac{a^{2} \sin α}{2}$ ;