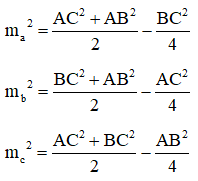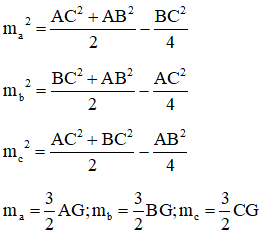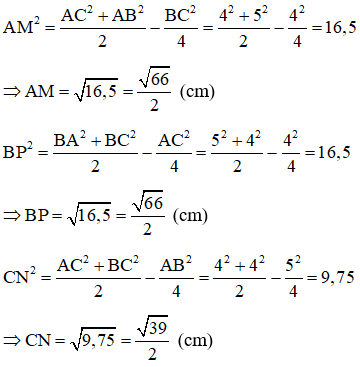Toptailieu.vn biên soạn và giới thiệu Công thức tính độ dài đường trung tuyến (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức tính độ dài đường trung tuyến (50 bài tập minh họa) HAY NHẤT 2024

I. Lí thuyết tổng hợp

- Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.

- Các đường trung tuyến của tam giác giao nhau tại trọng tâm của tam giác.

- Trong tam giác ABC cân tại A và M là trung điểm của BC thì đường trung tuyến AM cũng là đường cao, đường phân giác và đường trung trực.

- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

- Độ dài đường trung tuyến: Gọi $m_a,m_b,m_c$ là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:

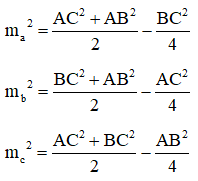
II. Các công thức

Cho tam giác ABC vuông tại A, M là trung điểm của BC ta có: $AM=\frac{1}{2}BC$.

Gọi $m_a,m_b,m_c$ là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:

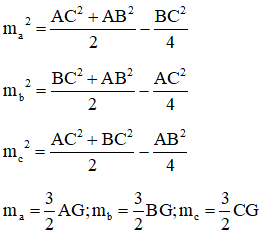
(với G là trọng tâm của tam giác ABC).

III. Ví dụ minh họa

Bài 1: Cho tam giác ABC có AB = 5cm, AC = 4cm và BC = 4cm. Các điểm M, N, P lần lượt là là trung điểm của BC, AB, AC. Tính độ dài AM, BP và CN.

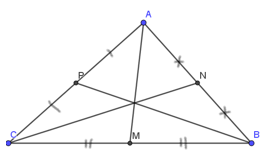
Lời giải:

Các điểm M, N, P lần lượt là là trung điểm của BC, AB, AC.

$\Rightarrow$ AM, BP, CN là các đường trung tuyến của tam giác ABC.

Xét tam giác ABC ta có:

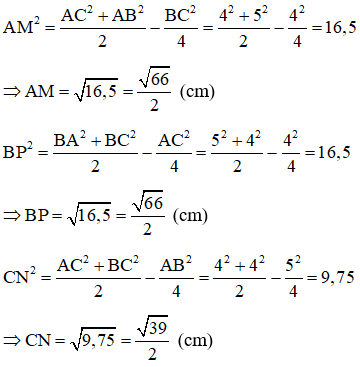
Bài 2: Cho tam giác ABC vuông tại A. Có BC = 10cm. Điểm M là trung điểm của BC. Tính độ dài AM.

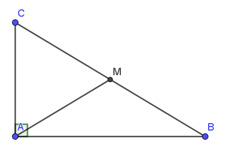
Lời giải:

Xét tam giác ABC vuông tại A có:

M là trung điểm của BC$\Rightarrow$ AM là đường trung tuyến ứng với cạnh huyền BC.

$\Rightarrow AM=\frac{1}{2}BC=\frac{1}{2}.10=5$ (cm)

Bài 3: Cho tam giác ABC có trọng tâm G, N là trung điểm của AB. Tính độ dài CN biết CG = 4cm.

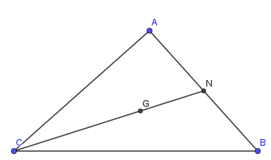
Lời giải:

Xét tam giác ABC có trọng tâm G ta có:

N là trung điểm BC $\Rightarrow$ CN là đường trung tuyến, điểm G nằm trên CN

Ta có:$CG=\frac{2}{3}CN$

$\Rightarrow CN=\frac{3}{2}CG=\frac{3}{2}.4=6$ (cm)

IV. Bài tập tự luyện 

Câu 1. Tam giác $ABC$ có $AB=6\text{cm},AC=8\text{cm}$ và $BC=10\text{cm}$. Độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác bằng:

A. $4\text{cm}$.           B. $\sqrt{3}\text{cm}$.             C. $7\text{cm}$.               D. $5\text{cm}$.

Câu 2. Tam giác $ABC$ vuông tại A và có $AB=AC=a$. Tính độ dài đường trung tuyến  của tam giác đã cho.

A. $BM=1,5a.$    B. $BM=a\sqrt{2}.$        C. $BM=a\sqrt{3}.$        D. $BM=\frac{a\sqrt{5}}{2}.$

Câu 3. Tam giác $ABC$ có $AB=9$cm, $AC=12$cm và $BC=15$cm. Tính độ dài đường trung tuyến AM của tam giác đã cho.

A. $AM=\frac{15}{2}$cm. B. $AM=10$cm.     C. $AM=9$cm.      D. $AM=\frac{13}{2}$cm.

Câu 4. Tam giác $ABC$ cân tại C, có $AB=9\text{cm}$ và $AC=\frac{15}{2}\text{cm}$. Gọi D là điểm đối xứng của B qua C. Tính độ dài cạnh AD

A. $AD=6$cm.   B. $AD=9$cm.       C. $AD=12$cm.      D. $AD=12\sqrt{2}$cm.

Câu 5. Tam giác $ABC$ có $AB=3,BC=8$. Gọi M là trung điểm của BC. Biết $\cos \widehat{AMB}=\frac{5\sqrt{13}}{26}$ và $AM>3$. Tính độ dài cạnh AC.

A. $AC=\sqrt{13}$.     B. $AC=\sqrt{7}$.          C. $AC=13$.          D. $AC=7$.

Câu 6. Tam giác $ABC$ có trọng tâm G. Hai trung tuyến $BM=6$, $CN=9$ và $\widehat{BGC}={120}^0$. Tính độ dài cạnh AB.

A. $AB=\sqrt{11}$.     B. $AB=\sqrt{13}$.         C. $AB=2\sqrt{11}$.       D. $AB=2\sqrt{13}$.

Câu 7. Tam giác $ABC$ có độ dài ba trung tuyến lần lượt là $9;12;15$. Diện tích của tam giác $ABC$ bằng:

A. $24$.                                        B. $24\sqrt{2}$.              C. $72$.    D. $72\sqrt{2}$.

Câu 8. Cho tam giác $ABC$ có $AB=c,BC=a,CA=b$. Nếu giữa $a,b,c$ có liên hệ $b^2+c^2=2a^2$ thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:

A. $\frac{a\sqrt{3}}{2}$.           B. $\frac{a\sqrt{3}}{3}$.               C. $2a\sqrt{3}$.              D. $3a\sqrt{3}$.

Câu 9. Cho hình bình hành $ABCD$ có $AB=a,BC=b,BD=m$ và $AC=n$. Trong các biểu thức sau, biểu thức nào đúng:

A. $m^2+n^2=3\left(a^2+b^2\right)$.                    B. $m^2+n^2=2\left(a^2+b^2\right)$.

C. $2\left(m^2+n^2\right)=a^2+b^2$.                    D. $3\left(m^2+n^2\right)=a^2+b^2$.

Câu 10. Tam giác $ABC$ có $AB=c,BC=a,CA=b$. Các cạnh $a,b,c$ liên hệ với nhau bởi đẳng thức $a^2+b^2=5c^2$. Góc giữa hai trung tuyến AM và BN là góc nào?

A. ${30}^0$.                                       B. ${45}^0$.                 C. ${60}^0$.      D. ${90}^0$.

Câu 11. Tam giác $ABC$ có ba đường trung tuyến $m_a,m_b,m_c$ thỏa mãn $5m_a^2=m_b^2+m_c^2$. Khi đó tam giác này là tam giác gì?

A. Tam giác cân.                                                  B. Tam giác đều.         

C. Tam giác vuông.                   D. Tam giác vuông cân.

Câu 12. Tam giác $ABC$ có $AB=c,BC=a,CA=b$. Gọi $m_a,m_b,m_c$ là độ dài ba đường trung tuyến, G trọng tâm. Xét các khẳng định sau:

. $m_a^2+m_b^2+m_c^2=\frac{3}{4}\left(a^2+b^2+c^2\right)$.      .$G{A}^2+G{B}^2+G{C}^2=\frac{1}{3}\left(a^2+b^2+c^2\right)$ .

Trong các khẳng định đã cho có

A. $\left(\text{I}\right)$ đúng.     B. Chỉ $\left(\text{II}\right)$ đúng. C. Cả hai cùng sai. D. Cả hai cùng đúng.

Câu 13. Cho tam giác ABC cân biết AB = AC = 10 cm, BC = 12 cm. M là trung điểm BC. Độ dài trung tuyến AM là :

A. 22 cm

B. 2 cm

C. 6 cm

D. 8 cm

Câu 14. Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là:

A. 4,5 cm

B. 3 cm

C. 6 cm

D. 4 cm

Câu 15. Cho tam giác ABC có hai đường trung tuyến BM và CN. Nếu BM = CN thì tam giác ABC là tam giác gì?

A. tam giác cân

B. tam giác vuông

C. tam giác đều 

D. tam giác vuông cân

Câu 16. Cho hai đường thẳng xx' và yy' gặp nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm giưac O và B, AB = 2 OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của đoạn thẳng Lm. Nối B với L, B và M và gọi P là trung điể của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB. Chứng minh các đoạn thẳng LP và MQ đi qua A.

Câu 17. Cho tam giác ABC có BM và Cn là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME = MG. Kéo dài CN lấy đoạn NF = NG. Chứng minh

a, EF = BC 

b, đường thẳng AG đi qua trung điểm BC.

Câu 18. Cho một tam giác ABC cân có AB = AC = 17 cm, BC = 16 cm. Hãy kẻ đường trung tuyến AM

a, Tính độ dài AM

b, Chứng minh AM vuông góc với BC

Câu 19. Cho điểm G là trọng tâm của tam giác đều ABC, hãy chứng minh rằng các cạnh GA, GB, GC bằng nhau.