Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Phương trình bậc nhất đối với hàm số lượng giác (HAY NHẤT 2024) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 11.
Phương pháp giải Phương trình bậc nhất đối với hàm số lượng giác (HAY NHẤT 2024)
1. Lý thuyết
Nhắc lại công thức nghiệm phương trình lượng giác
2. Các dạng bài tập
Dạng 1: Phương trình lượng giác sử dụng phân tích đa thức thành nhân tử đưa về phương trình tích
Phương pháp giải:
Sử dụng các biến đổi thích hợp để xuất hiện nhân tử chung như công thức nhân đôi, công thức nhân ba...
- Công thức nhân đôi:
sin2a = 2sina.cosa
cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
- Công thức nhân ba:
sin3a = 3sina – 4sin3a
cos3a = 4cos3a – 3cosa
Ví dụ minh họa:
Ví dụ 1: Giải các phương trình sau:
a) cosx – 2sin2x = 0
b) 6sin4x + 5sin8x = 0
c) cos2x – sin2x = 0
Lời giải
a) cosx – 2sin2x = 0
Vậy họ nghiệm của phương trình là
b) 6sin4x + 5sin8x = 0
Vậy họ nghiệm của phương trình là .
c) cos2x – sin2x = 0
Giải phương trình (*)
Trường hợp 1: cosx = 0. Thay vào (*) ta được sinx = 0
Ta thấy sin2x + cos2x = 02 + 02 = 0 (Vô lí) (Loại).
Trường hợp 2:
Chia hai vế của phương trình cho cosx, ta được
(Thỏa mãn)
Vậy họ nghiệm của phương trình là: .
Ví dụ 2: Giải phương trình: sinx.cos3x – sinx + 2cos3x – 2 = 0.
Lời giải
Ta có: sinx.cos3x – sinx + 2cos3x – 2 = 0
Vậy họ nghiệm của phương trình là: .
Dạng 2: Sử dụng công thức biến đổi tổng thành tích và tích thành tổng
Phương pháp giải:
- Công thức biến đổi tổng thành tích
- Công thức biến đổi tích thành tổng
Ví dụ minh họa:
Ví dụ 1: Giải các phương trình sau:
a) sin2x.sin5x = sin3x.sin4x
b) sin5x.cos3x = sin4x.cos2x
Lời giải
a) sin2x.sin5x = sin3x.sin4x
Vậy họ nghiệm của phương trình là: .
b) sin5x.cos3x = sin4x.cos2x
Vậy họ nghiệm của phương trình là: .
Ví dụ 2: Giải các phương trình sau:
a) sin3x + sin2x = sinx
b) sinx + sin3x = cos2x + cos4x
Lời giải
a) sin3x + sin2x = sinx
Vậy họ nghiệm của phương trình là: .
b) sinx + sin3x = cos2x + cos4x
Vậy họ nghiệm của phương trình là: .
Dạng 3: Sử dụng công thức hạ bậc
Phương pháp giải:
Công thức hạ bậc hai:
Ví dụ minh họa:
Ví dụ 1: Giải phương trình sau: sin2x + sin23x = 2sin22x.
Lời giải
Ta có: sin2x + sin23x = 2sin22x
Vậy họ nghiệm của phương trình là: .
Ví dụ 2: Giải phương trình sau: cos2x + cos22x + cos23x + cos24x = 2
Lời giải
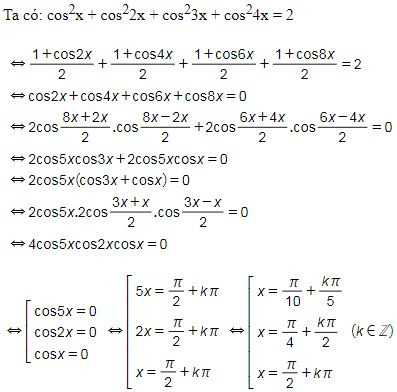
Vậy họ nghiệm của phương trình là .
3. Bài tập tự luyện
Câu 1. Nghiệm của phương trình cos2x – cosx = 0 thuộc khoảng là:
A.
B.
C.
D.
Câu 2. Giải phương trình cos2x – sin2x = 0
A.
B.
C.
D.
Câu 3. Nghiệm của phương trình sin2x – sinx = 2 – 4cosx là:
A.
B.
C.
D.
Câu 4. Nghiệm của phương trình sin x.cos x.cos2x = 0 là:
A.
B.
C.
D.
Câu 5. Nghiệm của phương trình cos3x – cos5x = sinx là:
A.
B.
C.
D.
Câu 6. Phương trình cos5x.cos3x = cos 4x.cos2x có tập nghiệm trùng với tập nghiệm của phương trình nào sau đây?
A. sinx = cos x
B. cosx = 0
C. cos8x = cos6x
D. sin8x = cos6x
Câu 7. Phương trình cosx + 3cos2x + cos3x = 0 có nghiệm là:
A.
B.
C.
D.
Câu 8. Nghiệm của phương trình cos3x – cos4x + cos5x = 0 là:
A.
B.
C.
D.
Câu 9. Phương trình 2sinx + cosx – sin2x – 1 = 0 có nghiệm là:
A.
B. ,
C. ,
D. ,
Câu 10. Một họ nghiệm của phương trình cos x.sin23x – cosx = 0 là:
A.
B.
C.
D.
Câu 11. Các nghiệm của phương trình sin2x + sin23x = cos2x + cos23x là:
A.
B.
C.
D.
Câu 12. Các nghiệm của phương trình (với ) là:
A.
B.
C.
D.
Câu 13. Họ nghiệm của phương trình sin2x + cos24x = 1 là:
A.
B.
C.
D.
4. Bài tập ứng dụng
Câu 1. Nghiệm của phương trình √12+2tanx=0 là:
A. π/6+kπ
B. (-π)/3+kπ
C. (-π)/6+kπ
D. (-π)/6+k2π
Lời giải
Chọn C
Ta có: √12+2tanx=0 ⇔ 2√3+2tanx=0
⇔ tan x= - √3 ⇔ tanx= tan (- π)/3
⇔ x= (-π)/3+kπ
Câu 2: Tìm nghiệm của phương trình:
A.
B.
C.
D.
Lời giải
Chọn A.
Ta có:
Câu 3: Cho phương trình 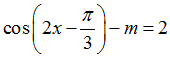
A. Không tồn tại m.
B.m ϵ[-1;3] .
C. m ϵ[-3;-1]
D. mọi giá trị của m.
Lời giải
Chọn C.
Ta có:
Với mọi x ta luôn có: - 1 ≤ cos( 2x- π/3) ≤ 1
Do đó phương trình có nghiệm khi và chỉ khi:
-1 ≤ m+2 ≤ 1 hay-3 ≤ m ≤ -1
Câu 4: Họ nghiệm của phương trình cot(x+π/3)+1=0 là
A.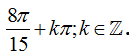
B.
C.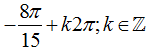
D.
Lời giải
Chọn B.
Câu 5: Nghiệm của phương trình 3cot x+ √3=0là:
A.
B.
C.
D. x= (-π)/3+kπ.
Lời giải
Chọn D.
Câu 6: Phương trình 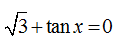
A.
B.
C.
D.
Lời giải
Ta có: √3+tanx=0
Chọn B.
Câu 7: Giải phương trình : 2tanx+ 10= 0
A. x= arctan 5+ k.π
B. x = arctan -5+ kπ
C. x= - 5+kπ
D. x= 1/5+kπ
Lời giải
Ta có: 2tanx + 10 = 0 ⇒ 2tanx= - 10
⇒ tanx= - 5.
Sử dụng công thức nghiệm tổng quát của phương trình
Suy ra:Nghiệm của phương trình đã cho là: x= arctan-5+ kπ; k∈Z
Câu 8: Giải phương trình : 1/2.cot( x+3π/4)=0.
A. (-π)/4+kπ.
B. π/4+kπ.
C. π/2+kπ.
D. π/3+kπ
Lời giải
Ta có: 1/2.cot( x+3π/4)=0 ⇒ cot( x+3π/4)=0.
⇒ cot(x+ 3π/4)=cot π/2
⇒ x+ 3π/4= π/2+kπ ⇒ x= (-π)/4+kπ
Chon A.
Câu 9: Nghiệm của phương trình
A.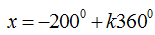
B.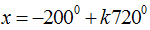
C.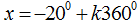
D.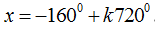
Lời giải
Chọn D.
Câu 10. Giải phương trình : 2cos(x+ 300) + 1= 0
A.
B.
C.
D.
Lời giải
Ta có: 2cos(x+300)+ 1= 0 ⇒ 2cos(x+ 300) = - 1
⇒ cos( x+ 300)= -1/2 = cos1200
Chọn B.
Câu 11: Giải phương trình : 2sin( x – 100) – sin900 = 0
A.
B.
C.
D. Một đáp án khác
Lời giải
Ta có: 2sin(x- 100) - sin 900= 0
⇒ 2sin(x – 100) = sin900 = 1
⇒ sin( x- 100) = 1/2 = sin300
Chọn C.
Ví dụ 12.Giải phương trình 2cos(x+ 100) + 10= 0
Lời giải
Ta có : 2cos(x+ 100) + 10= 0
⇒ 2cos(x+ 100) = - 10
⇒ cos( x+ 100) = - 5 (*)
Do với mọi x ta luôn có: - 1 ≤ cos(x+ 100 ) ≤ 1 nên từ (*) suy ra phương trình (*) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
Câu 12: Giải phương trình 2cos( 1200 - x)+ 1= 0
A.
B.
C.
D.
Lời giải:
Ta có: 2cos (1200- x) + 1 = 0
⇒ 2cos(1200 – x) = - 1
⇒ cos(1200-x) = (- 1)/2=cos1200
Vậy phương trình đã cho có nghiệm là:
Câu 13: Giải phương trình: 3sin(x- π/5)+3=0
Lời giải:
Ta có:
Chọn C.
Câu 14: Giải phương trình: √2 tan( x- 150 )- √2=0
A. 300+ k. 1800
B.450+ k.3600
C.450+ k.1800
D. 600+ k. 1800
Lời giải
Lời giải:
Ta có: √2 tan( x- 150 )- √2=0
⇒ √2 tan( x- 150 )= √2
⇒ tan (x- 150) = 1= tan 450
⇒ x- 150 = 450+ k. 1800
⇒ x = 600+ k.1800
Vậy nghiệm của phương trình đã cho là x= 600+ k. 1800
Chọn D.
Câu 15: Giải phương trình 3 cot(x+ 2π/5)- √3=0
A.
B.
C.
D.
Lời giải:
Ta có:
Chọn B.
Câu 16: Giải phương trình 2tanx – 6= 0
A. x= 3+ k. π
B. x = - 3+ kπ
C.x= arctan 3+ kπ
D. Phương trình vô nghiệm
Lời giải:
Ta có: 2tanx – 6= 0 ⇒ 2tanx = 6
⇒ tan x= 3
⇒ x = arcrtan 3+ k.π
Chọn C.
Câu 17: Giải phương trình
A.
B.
C.
D.Phương trình vô nghiệm
Lời giải:
Chọn A.
Câu 18: Giải phương trình 3sin(x+ 100) - 1=0
A.
B.
C.
D.
Lời giải:
Ta có; 3sin(x+ 100) - 1= 0
Chọn D.
Câu 19: Giải phương trình √3 sin( x+π/10)+3=0
A. x= π/10+k2π
B. x= -π/10+k2π
C. Phương trình vô nghiệm
D. Đáp án khác
Lời giải:
Kết hợp với (*) suy ra phương trình đã cho vô nghiệm
Chọn D.
Câu 20: Giải phương trình: 2sin( x+π/6) – cos 3π/2=0
Lời giải:
Chọn A.
Câu 21: Giải phương trình : 2sin(x+ π/8)-10=0
A.
B.
C.
D.
Lời giải:
Chọn B.
Xem thêm các dạng Toán 11 hay, chọn lọc khác:
Tìm tập xác định, tập giá trị của hàm số lượng giác và cách giải
Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác và cách giải
Cách tính GTNN - GTLN của hàm số lượng giác chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.