Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Công thức Chứng minh đường thẳng song song với mặt phẳng (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải Công thức Chứng minh đường thẳng song song với mặt phẳng (HAY NHẤT 2024)

1. Lý thuyết

a) Vị trí tương đối của đường thẳng d và mặt phẳng $\left(\alpha \right)$.

Tùy theo số giao điểm chung của d và $\left(\alpha \right)$, ta có 3 trường hợp sau:

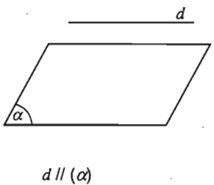
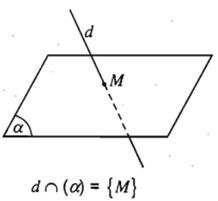
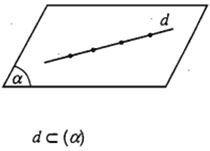
b) Tính chất

Định lý 1:

Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).

Tức là: $\left\{\begin{array}{l}a\not\subset \left(P\right)\\ a\parallel d\\ d\subset \left(P\right)\end{array}\right.$$\Rightarrow a\parallel \left(P\right).$

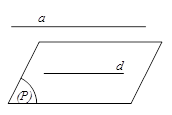
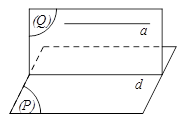
Định lý 2:

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo một giao tuyến d thì a song song với d.

Tức là: $\left\{\begin{array}{l}a\parallel \left(P\right)\\ a\subset \left(Q\right)\\ \left(Q\right)\cap \left(P\right)=d\end{array}\right.$$\Rightarrow a\parallel d.$

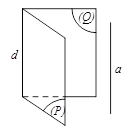
Hệ quả:

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến (nếu có) của chúng song song với đường thẳng đó.

Tức là: $\left\{\begin{array}{l}\left(P\right)\cap \left(Q\right)=d\\ \left(P\right)\parallel a\\ \left(Q\right)\parallel a\end{array}\right.$$\Rightarrow d\parallel a.$

Định lý 3:

Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

2. Công thức

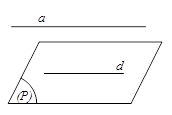
Phương pháp chứng minh đường thẳng song song với mặt phẳng

Để chứng minh đường thẳng a song song với (P), ta chứng minh a song song với một đường thẳng d nằm trong (P)

Tức là: $\left\{\begin{array}{l}a\not\subset \left(P\right)\\ a\parallel d\\ d\subset \left(P\right)\end{array}\right.$$\Rightarrow a\parallel \left(P\right).$

3. Ví dụ minh họa

Ví dụ 1: Cho tứ diện ABCD. Lấy G là trọng tâm tam giác ABD. Gọi M là một điểm trên cạnh BC sao cho MB = 2MC. Chứng minh MG // (ACD).

Lời giải

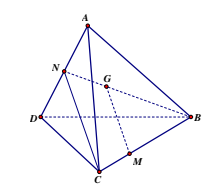
Gọi N là trung điểm của AD

+ Vì G là trọng tâm tam giác ABD nên $\frac{BG}{BN}=\frac{2}{3}$

+ Xét tam giác BCN có: $\frac{BM}{BC}=\frac{BG}{BN}=\frac{2}{3}$ nên MG // NC

Ta có:$\left\{\begin{array}{l}MG\not\subset \left(ACD\right)\\ MG//NC\\ NC\subset \left(ACD\right)\end{array}\right.$$\Rightarrow MG//\left(ACD\right)$

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm tam giác SAB, I là trung điểm của AB và M là điểm trên cạnh AD sao cho $AM=\frac{1}{3}AD$

a) Đường thẳng đi qua M và song song với AB cắt CI tại N. Chứng minh NG // (SCD).

b) Chứng minh MG // (SCD).

Lời giải

a) + Hình bình hành ABCD có MJ // AB // CD và $\frac{AM}{AD}=\frac{1}{3}$

Nên $\frac{IN}{IC}=\frac{BJ}{BC}=\frac{AM}{AD}=\frac{1}{3}$

+ G là trọng tâm tam giác SAB nên $\frac{IG}{IS}=\frac{1}{3}$

+ Xét tam giác ISC có: $\frac{IG}{IS}=\frac{IN}{IC}=\frac{1}{3}$ nên GN // SC

Ta có:$\left\{\begin{array}{l}GN\not\subset \left(SCD\right)\\ GN//SC\\ SC\subset \left(SCD\right)\end{array}\right.$$\Rightarrow GN//\left(SCD\right)$

b) Kéo dài MI cắt CD tại E

+ Ta có AI // ED nên $\frac{IM}{IE}=\frac{AM}{MD}=\frac{1}{2}$

+ Xét tam giác SIE có: $\frac{IM}{EM}=\frac{IG}{GS}=\frac{1}{2}$ nên MG // SE

Ta có:$\left\{\begin{array}{l}MG\not\subset \left(SCD\right)\\ MG//SE\\ SE\subset \left(SCD\right)\end{array}\right.$$\Rightarrow MG//\left(SCD\right)$

4. Bài tập vận dụng 

Câu 1. Cho hình chóp tứ giác S.ABCD. Gọi M và N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?

A. MN // (ABCD)

B. MN // (SAB)

C. MN // (SCD)

D. MN // (SBC)

Câu 2. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, Q thuộc cạnh AB sao cho AQ = 2QB, P là trung điểm của AB. Khẳng định nào sau đây đúng?

A. MN // (BCD)

B. QG // (BCD)

C. MN cắt (BCD)

D. Q thuộc mặt phẳng (BCD)

Câu 3: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Mặt phẳng (α) qua BD và song song với SA, mặt phẳng (α) cắt SC tại K. Khẳng định nào sau đây là khẳng định đúng ?

A. SK = 2KC      B. SK = 3KC        C. SK = KC       D. SK = (1/2)KC

Câu 4: Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Gọi mặt phẳng (α) qua và M song song với AB và CD. Mặt phẳng (α) cắt BC; BD; AD lần lượt tại N; P, Q. Tìm mệnh đề đúng?

A. PQ // mp(ABC)      B. MN // mp(ABD)     C. NP // (AQC)      D. PQ // BC

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm AB; CD và SA. Gọi giao tuyến của mp(MNP) và mp(SAD) là PQ (Q ∈ SD). Tìm mặt phẳng song song với SC?

A. (APQ)        B. (BMQ)        C. (PNB)         D. (PQN)

Câu 6: Cho hình chóp S.ABC có SA = SB = AB = a; SC = AC = 2a. Gọi G là trọng tâm tam giác SAC và H là trực tâm tam giác SAB. Gọi M là trung điểm SA và N là trung điểm của BC. Tìm đường thẳng song song với mp(ABC)?

A. GH         B. HN        C. GM        D. HM

Câu 7: Cho hình chóp S. ABCD. Trong tam giác SAB có ∠SAB = 90°; SA = SB đường cao AH. Lấy điểm M trên cạnh SA sao cho: SM = 3MD. Trên cạnh SC lấy điểm N sao cho NC = 3NS. Gọi K là trung điểm của SD. Tìm đường thẳng song song với mp(ABCD).

A. HN        B. KM         C. MN        D. HK

Câu 8: Cho hình chóp S.ABCD. Trên các cạnh AD; AB; SB; SD lần lượt lấy các điểm M; N; P; Q sao cho MQ // NP và MQ = NP. Tìm mặt phẳng song song với đường thẳng PQ.

A. (SMD)

B. (PNC)

C. (DCN)

D. Không có mặt phẳng nào song song PQ

5. Bài tập tự luyện

Câu 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O , I là trung điểm cạnh SC. Khẳng định nào sau đây SAI?

A. IO // mp(SAB)

B. IO // mp(SAD)

C. mp(IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác

D. (IBD) ∩ (SAC) = IO

Lời giải:

Chọn C

   + Xét tam giác SAC có I và O lần lượt là trung điểm của SC và AC nên IO là đường trung bình của tam giác SAC

⇒ IO // SA

   + Ta có: mp(IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai

   + Ta có: (IBD) ∩ (SAC) = IO nên D đúng.

Câu 2: Cho tứ diện ABCD. Gọi G₁ và G₂ lần lượt là trọng tâm các tam giác BCD và ACD. Chọn mệnh đề sai:

A. G₁G₂ // (ABD)

B. G₁G₂ // (ABC)

C. BG₁, AG₂ và CD đồng quy

D. G₁G₂ = (2/3)AB

Lời giải:

Chọn D

   + Do G₁ và G₂ lần lượt là trọng tâm các tam giác BCD và ACD nên BG₁; AG₂ và CD đồng qui tại M (M là trung điểm của CD)

⇒ C đúng

   + Xét tam giác AMB có:

(MG₁)/MB = (MG₂)/MA = 1/3 (tính chất trọng tâm tam giác)

⇒ G₁G₂ // AB (định lí Ta let đảo)

⇒ A đúng

⇒ B đúng

Chọn D

Câu 3: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Mặt phẳng (α) qua BD và song song với SA, mặt phẳng (α) cắt SC tại K. Khẳng định nào sau đây là khẳng định đúng ?

A. SK = 2KC      B. SK = 3KC        C. SK = KC       D. SK = (1/2)KC

Lời giải:

Chọn C

   + Gọi O là giao điểm của AC và BD

Do mặt phẳng (α) qua BD nên O ∈ (α)

   + Trong tam giác SAC, kẻ OK // SA (k ∈ SC)

   + Trong tam giác SAC ta có

 là đường trung bình của ΔSAC

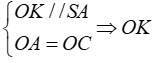
Vậy SK = KC

Câu 4: Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Gọi mặt phẳng (α) qua và M song song với AB và CD. Mặt phẳng (α) cắt BC; BD; AD lần lượt tại N; P, Q. Tìm mệnh đề đúng?

A. PQ // mp(ABC)      B. MN // mp(ABD)     C. NP // (AQC)      D. PQ // BC

Lời giải:

Chọn D

   + Trên mp(ABC) kẻ MN // AB; N ∈ BC

   + Trên mp( BCD) kẻ NP // CD; P ∈ BD

⇒ (α) chính là mặt phẳng (MNP)

   + Ta tìm giao tuyến của mp( MNP) và ( ABD)

nên (MNP) ∩ (ABD) = PQ // MN // AB

⇒ PQ // mp(ABC); A đúng

   + theo cách dựng, MN // AB mà AB ⊂ (ABD)

⇒ MN // (ABD); B đúng

   + Theo cách dựng NP // CD mà CD ⊂ (AQC)

⇒ NP // mp(AQC); C đúng

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm AB; CD và SA. Gọi giao tuyến của mp(MNP) và mp(SAD) là PQ (Q ∈ SD). Tìm mặt phẳng song song với SC?

A. (APQ)        B. (BMQ)        C. (PNB)         D. (PQN)

Lời giải:

   + Xét tứ giác ABCD có M và N lần lượt là trung điểm của AB và DC

⇒ MN là đường trung bình của hình ABCD

⇒ MN // AD // BC

   + Xét giao tuyến của (MNP) và (SAD):

Trong mp(SAD); dựng Px // AD cắt SD tại Q

   + Ta có: PQ // AD và P là trung điểm của SA

⇒ Q là trung điểm của SD.

   + Xét mp(SCD) có N và Q lần lượt là trung điểm của CD; SD nên NQ // SC

Mà NP ⊂ mp(PQN) nên SC // mp(PQN)

Chọn D

Câu 6: Cho hình chóp S.ABC có SA = SB = AB = a; SC = AC = 2a. Gọi G là trọng tâm tam giác SAC và H là trực tâm tam giác SAB. Gọi M là trung điểm SA và N là trung điểm của BC. Tìm đường thẳng song song với mp(ABC)?

A. GH         B. HN        C. GM        D. HM

Lời giải:

   + Xét tam giác SAB có; SA = SB = AB = a

⇒ tam giác SAB là tam giác đều nên trực tâm H đồng thời là trọng tâm của tam giác SAB.

   + Gọi I và T lần lượt là trung điểm của AB; AC

Do G và H là trọng tâm hai tam giác SAC và SAB nên :

SH/SI = SG/ST = 2/3

⇒ HG // IT

   + Mà IT ⊂ mp (ABC) nên HG // mp(ABC)

Chọn A

Câu 7: Cho hình chóp S. ABCD. Trong tam giác SAB có ∠SAB = 90°; SA = SB đường cao AH. Lấy điểm M trên cạnh SA sao cho: SM = 3MD. Trên cạnh SC lấy điểm N sao cho NC = 3NS. Gọi K là trung điểm của SD. Tìm đường thẳng song song với mp(ABCD).

A. HN        B. KM         C. MN        D. HK

Lời giải:

   + Xét tam giác SAB có: ∠SAB = 90° ; SA = SB

⇒ Tam giác SAB vuông cân tại S.

Mà AH là đường cao nên đồng thời là đường trung tuyến nên H là trung điểm của SB

   + Xét tam giác SBD có: H và K lần lượt là trung điểm của SB; SD⇒ HK là đường trung bình của tam giác SBD nên HK // BD

Mà BD ⊂ mp(ABCD) nên : HK // mp(ABCD)

Chọn D

Câu 8: Cho hình chóp S.ABCD. Trên các cạnh AD; AB; SB; SD lần lượt lấy các điểm M; N; P; Q sao cho MQ // NP và MQ = NP. Tìm mặt phẳng song song với đường thẳng PQ.

A. (SMD)

B. (PNC)

C. (DCN)

D. Không có mặt phẳng nào song song PQ

Lời giải:

   + Ta có; MQ // NP

⇒ bốn điểm M; N; P và Q đồng phẳng

   + Xét tứ giác MNPQ có: MQ // NP và MQ = NP

⇒ Tứ giác MNPQ là hình bình hành

⇒ MN // PQ

   + Mà MN ⊂ mp(DCN)

⇒ MN // mp(DCN)

Chọn C

Xem các Phương pháp giải bài tập hay, chi tiết khác :

Công thức Chứng minh hai mặt phẳng song song

Định lý Ta-lét trong không gian

Hai mặt phẳng song song và cách giải bài tập

Công thức Giao tuyến của ba mặt phẳng và hệ quả

Công thức Chứng minh hai đường thẳng song song trong không gian