Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Định lý Ta-lét trong không gian (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:
Nội dung bài viết
Phương pháp giải Định lý Ta-lét trong không gian (HAY NHẤT 2024)
1. Lý thuyết
+ Định lý Ta – let
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
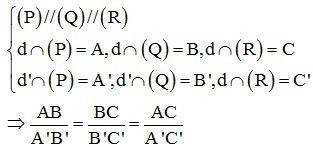
+ Định lý Ta-lét đảo:
Cho hai đường thẳng d và d’ chéo nhau và các điểm A, B, C trên d, các điểm A’, B’, C’ trên d’ sao cho ABA'B'=BCB'C'=ACA'C'. Khi đó các đường thẳng AA’, BB’, CC’ cùng song song với một mặt phẳng.
2. Công thức giải
Áp dụng định lý Ta–lét (thuận và đảo) để chứng minh tỉ lệ đoạn thẳng và chứng minh tồn tại mặt phẳng song song với các đường thẳng.
3. Ví dụ minh họa
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, ^BAC=30° Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?
Lời giải
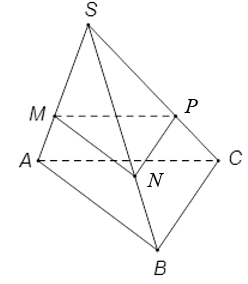
Diện tích tam giác ABC là
Gọi N, P lần lượt là giao điểm của mặt phẳng (P) và các cạnh SB, SC.
Vì (P) // (ABC) nên theo định lý Talet, ta có
Khi đó (P) cắt hình chóp S.ABC theo thiết diện là tam giác MNP đồng dạng với tam giác ABC theo tỉ số
Do đó
Vậy
Ví dụ 2: Cho tứ diện ABCD. Gọi I, J là hai điểm di động lần lượt trên các cạnh AD, BC sao cho . Chứng minh rằng: IJ luôn song song với một mặt phẳng cố định.
Lời giải
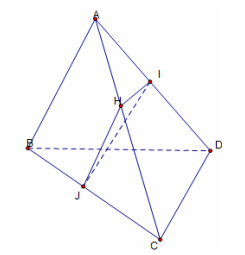
Trong (ACD): dựng IH // CD với
Xét tam giác ACD có HI // CD nên
Mà , do đó
Xét tam giác ABC có nên HJ // AB.
Dựng mặt phẳng (P) đi qua CD và song song với AB. Ta có mặt phẳng (P) cố định.
Ta có: và có
Do đó mà
Vậy IJ song song với mặt phẳng cố định.
4. Bài tập vận dụng
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm của SA và J, K là các điểm trên SB, SC sao cho JS = 2JB, KS = 2KC. Đường thẳng SD cắt mặt phẳng (IJK) tại M; E là giao điểm của hai đường thẳng IJ và KM. Tỉ số bằng
A.
B.
C.
D.
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’, đường thẳng SD cắt mặt phẳng (A’B’C’) tại D’. Gọi O là giao điểm của AC và BD, đường thẳng A’C’ cắt SO tại I. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Bài 3: Cho AB/A'B' = CD/C'D'
⇔ AB.C'D' = A'B'.CD ( I )
⇔ AB/CD = A'B'/C'D' ( II )
A. ( I ),( II ) đều sai.
B. ( I ),( II ) đều đúng.
C. Chỉ có ( I ) đúng
D. Chỉ có ( II ) đúng.
Bài 4: Cho các đoạn thẳng AB = 6cm, CD = 4cm, PQ = 8cm, EF = 10cm, MN = 25mm, RS = 15mm. Hãy chọn phát biểu đúng trong các phát biểu sau?
A. Đoạn AB và PQ tỉ lệ với hai đoạn thẳng EF vs RS.
B. Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN
C. Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF
D. Cả 3 phát biểu đều sai.
Bài 5: Cho các đoạn thẳng AB = 8cm, AC = 6cm, MN = 12cm, PQ = x cm. Tìm x để AB và CD tỉ lệ với MN và PQ?
Bài 6: Cho tam giác ABC, trên AB lấy điểm M sao cho AM = 4cm và MB = 6cm . Qua M kẻ đường thẳng song song với BC cắt AC tại N biết AC = 20cm . Tính AN?
A. 8cm B. 10cm
C. 12cm D. 6cm
Bài 7: Cho ba điểm A, B và C thẳng hàng sao cho B nằm giữa A và C. Có AB = 7cm và 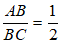
A. 14cm B. 7cm
C. 21cm D. 28cm
Bài 8: Cho tam giác ABC cân tại A có AB = 10cm. Lấy điểm M trên đoạn AB sao cho AM = 4cm, qua M kẻ đường thẳng d song song với BC cắt AC tại N. Tính tỉ số AN và AC?
Bài 9: Cho tam giác ABC vuông tại A có AB = 4cm, AC =3cm. Trên đoạn thẳng AB lấy điểm M sao cho AM = 1cm. Dựng đường thẳng MN vuông góc AB. Tính BN
Bài 10: Cho tam giác ABC, một đường thẳng d song song với BC cắt AB và AC theo thứ tự tại M và N biết 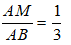
Bài 11: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Bài 12: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Bài 13: Chọn câu trả lời đúng. Cho hình bên, biết DE // AC, tìm x:
A. x = 6,5
B. x = 6,25
C. x = 5
D. x = 8
Bài 14: Chọn câu trả lời đúng. Cho hình bên biết ED ⊥ AB, AC ⊥ AB, tìm x:
A. x = 3
B. x = 2,5
C. x = 2
D. x = 4
Bài 15: Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
A. 6 cm
B. 5 cm
C. 4 cm
D. 7 cm
5. Bài tập tự luyện
Bài 1: Tính x trong trường hợp sau biết rằng FG // HT :
A. x = 4,5
B. x = 3
C. x = 2
D. Cả 3 đáp án trên đều sai
Áp dụng hệ quả của định lí Ta – lét với FG//HT ta có:
FG//HT ⇒ = EG/HE ⇔ ET =
=
= 4,5
Chọn đáp án A.
Bài 2: Cho hình bên. Chọn câu trả lời đúng?
A.
B.
C.
D. Cả 3 đáp án đều sai.
Ta có:
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
Bài 3: Cho hình bên. Chọn câu trả lời đúng?
A. ⇒ SH//LI
B. ⇒ SH//LI
C. ⇒ SH//LI
D. ⇒ SH//LI
Ta có:
+ → SH//LI
+ → SH//LI
Chọn đáp án B.
Bài 4: Cho Δ ABC có độ dài các cạnh như hình vẽ Kết quả nào sau đây đúng?
A. = 1,5
B. =
C.
D. Cả 3 đáp án đều sai.
Ta có:
Chọn đáp án C.
Bài 5: Cho tam giác ABC có AB = 4,5 cm. Một đường thẳng d cắt đoạn AB, AC lần lượt tại M và N sao cho AM = 1,5cm, AN = 2 cm và NC = 5cm. Tìm khẳng định sai ?
A. MN// BC
B. MB = 3cm
C. Đường thẳng MN và BC có điểm chung.
D.
Vì điểm M nằm giữa hai điểm A và B nên:
MB = AB – AM = 4,5 - 1,5 = 3cm
Ta có:
Do đó, đường thẳng MN không song song với BC.
Chọn đáp án A
Bài 6: Cho tam giác ABC, một đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N sao cho AM = 13cm, MB = 11cm và MN = 8cm. Tính BC
Do M nằm giữa A và B nên: AB = AM + MB = 13 + 11 = 24 cm
Theo hệ quả định lí Ta let ta có:
Chọn đáp án C
Bài 7: Cho tam giác ABC, một đường thẳng d cắt 2 cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 5cm, AN = 6 cm và AC = 13,5cm; BC = 12 cm . Tính MN?
Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
Chọn đáp án B
Bài 8: Cho tam giác ABC, đường thẳng d song song BC cắt hai cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 8cm và BC = 36cm. Tính MN?
A. 10cm
B. 8cm
C. 12cm
D. Đáp án
Điểm M nằm giữa A và B nên: AB = AM + MB = 4 + 8 = 12cm
Áp dụng hệ quả định lí Ta let ta có;
Chọn đáp án C
Bài 9: Cho tam giác MNP, đường thẳng d song song với NP cắt hai cạnh MN và MP lần lượt tại R và Q. Chu vi tam giác MNP là 60cm và chu vi tam giác MQR là 20cm, PN = 12cm . Tính RQ?
A. 2cm
B. 2,5cm
C. 3cm
D. 4cm
Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Chọn đáp án D
Bài 10: Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng 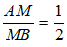
Ta có:
Vì MN// BC nên theo hệ quả định lí Ta let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Do đó, tỉ số chu vi tam giác AMN và ABC là
Chọn đáp án A
Bài 1: Tính x trong trường hợp sau biết rằng FG // HT :
A. x = 4,5
B. x = 3
C. x = 2
D. Cả 3 đáp án trên đều sai
Áp dụng hệ quả của định lí Ta – lét với FG//HT ta có:
FG//HT ⇒ = EG/HE ⇔ ET =
=
= 4,5
Chọn đáp án A.
Bài 2: Cho hình bên. Chọn câu trả lời đúng?
A.
B.
C.
D. Cả 3 đáp án đều sai.
Ta có:
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
Bài 3: Cho hình bên. Chọn câu trả lời đúng?
A. ⇒ SH//LI
B. ⇒ SH//LI
C. ⇒ SH//LI
D. ⇒ SH//LI
Ta có:
+ → SH//LI
+ → SH//LI
Chọn đáp án B.
Bài 4: Cho Δ ABC có độ dài các cạnh như hình vẽ Kết quả nào sau đây đúng?
A. = 1,5
B. =
C.
D. Cả 3 đáp án đều sai.
Ta có:
Chọn đáp án C.
Bài 5: Cho tam giác ABC có AB = 4,5 cm. Một đường thẳng d cắt đoạn AB, AC lần lượt tại M và N sao cho AM = 1,5cm, AN = 2 cm và NC = 5cm. Tìm khẳng định sai ?
A. MN// BC
B. MB = 3cm
C. Đường thẳng MN và BC có điểm chung.
D.
Vì điểm M nằm giữa hai điểm A và B nên:
MB = AB – AM = 4,5 - 1,5 = 3cm
Ta có:
Do đó, đường thẳng MN không song song với BC.
Chọn đáp án A
Bài 6: Cho tam giác ABC, một đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N sao cho AM = 13cm, MB = 11cm và MN = 8cm. Tính BC
Do M nằm giữa A và B nên: AB = AM + MB = 13 + 11 = 24 cm
Theo hệ quả định lí Ta let ta có:
Chọn đáp án C
Bài 7: Cho tam giác ABC, một đường thẳng d cắt 2 cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 5cm, AN = 6 cm và AC = 13,5cm; BC = 12 cm . Tính MN?
Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
Chọn đáp án B
Bài 8: Cho tam giác ABC, đường thẳng d song song BC cắt hai cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 8cm và BC = 36cm. Tính MN?
A. 10cm
B. 8cm
C. 12cm
D. Đáp án
Điểm M nằm giữa A và B nên: AB = AM + MB = 4 + 8 = 12cm
Áp dụng hệ quả định lí Ta let ta có;
Chọn đáp án C
Bài 9: Cho tam giác MNP, đường thẳng d song song với NP cắt hai cạnh MN và MP lần lượt tại R và Q. Chu vi tam giác MNP là 60cm và chu vi tam giác MQR là 20cm, PN = 12cm . Tính RQ?
A. 2cm
B. 2,5cm
C. 3cm
D. 4cm
Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Chọn đáp án D
Bài 10: Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng 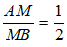
Ta có:
Vì MN// BC nên theo hệ quả định lí Ta let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Do đó, tỉ số chu vi tam giác AMN và ABC là
Chọn đáp án A
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Hai mặt phẳng song song và cách giải bài tập
Công thức Giao tuyến của ba mặt phẳng và hệ quả
Công thức Chứng minh hai đường thẳng song song trong không gian
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.