Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố

Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố

Hoàng Huyền Trang Ngày: 04-10-2022 Lớp 10

1.5 K

Với giải Vận dụng 2 trang 77 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3. Giải tam giác và ứng dụng thực tế giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố

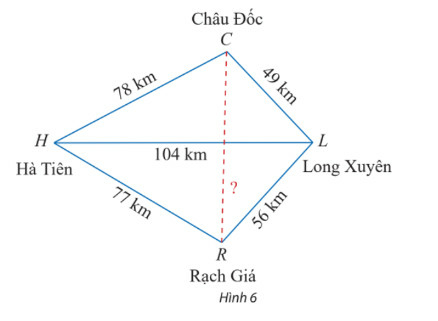
Vận dụng 2 trang 77 Toán 10 Tập 1: Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Vận dụng 2 trang 77 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc $\hat{C H L}, \hat{L H R}$ $\cos \hat{C H L} = \frac{C H^{2} + H L^{2} - C L^{2}}{2. C H . H L}; \cos \hat{L H R} = \frac{H L^{2} + H R^{2} - R L^{2}}{2. H L . H R}$

Bước 2: Áp dụng định lí cosin $C R^{2} = H C^{2} + H R^{2} - 2. H C . H R \cos \hat{C H R}$

Lời giải

Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có: $\begin{array}{l} \cos \hat{C H L} = \frac{C H^{2} + H L^{2} - C L^{2}}{2. C H . H L} = \frac{78^{2} + 104^{2} - 49^{2}}{2.78.104} = \frac{4833}{5408} \\ \Rightarrow \hat{C H L} \approx 26^{o} 39^{'} 40, 05^{″} \end{array}$

Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có: $\begin{array}{l} \cos \hat{L H R} = \frac{H L^{2} + H R^{2} - L R^{2}}{2. H L . H R} = \frac{104^{2} + 77^{2} - 56^{2}}{2.104.77} = \frac{13609}{16016} \\ \Rightarrow \hat{L H R} \approx 31^{o} 49^{'} 10, 4^{″} \\ \Rightarrow \hat{C H R} \approx 58^{o} 28^{'} 50, 45^{″} \end{array}$

Bước 2: Áp dụng định lí cosin $C R^{2} = H C^{2} + H R^{2} - 2. H C . H R \cos \hat{C H R}$

$\begin{array}{l} \Leftrightarrow C R^{2} = 78^{2} + 77^{2} - 2.78.77 \cos 58^{o} 28^{'} 50, 45^{″} \\ \Rightarrow C R \approx 75, 72 \end{array}$

Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khởi động trang 74 Toán 10 Tập 1:..

Thực hành trang 75 Toán 10 Tập 1: Giải tam giác ABC trong các trường hợp sau:..

Vận dụng 1 trang 76 Toán 10 Tập 1: Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc $25^{o}$ về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao...

Bài 1 trang 77 Toán 10 Tập 1: Giải tam giác ABC trong các trường hợp sau...

Bài 2 trang 77 Toán 10 Tập 1: Để lắp đường dây diện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là . Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B...

Bài 3 trang 77 Toán 10 Tập 1: Một người đứng cách thân một các quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5m...

Bài 4 trang 78 Toán 10 Tập 1: Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là và (Hình 9)...

Bài 5 trang 78 Toán 10 Tập 1: Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là . Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu đó là . Tính khoảng cách từ Q đến khinh khí cầu...

Bài 6 trang 78 Toán 10 Tập 1: Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là , góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là và đến điểm mốc khác là (Hình 11). Tính khoảng cách giữa hai cột mốc này...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

216

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

256

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

277

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

229

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.