Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài Ôn tập chương 1 - Tứ giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài Ôn tập chương 1 - Tứ giác

Bài 157 Trang 99 SBT Toán 8 Tập 1 Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

b. Hình thoi

c. Hình vuông

Phương pháp giải:

- Nhẩm lại dấu hiệu nhận biết và tính chất của hình chữ nhật, hình thoi và hình vuông.

Lời giải:

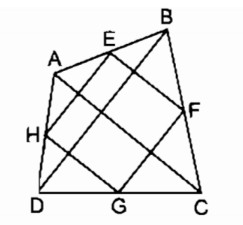
Trong ∆ ABC ta có EF là đường trung bình nên EF // AC và EF = ${\displaystyle \frac{1}{2}}$AC (1)

Trong ∆ ADC ta có HG là đường trung bình nên HG // AC và HG = ${\displaystyle \frac{1}{2}}$AC (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành

a. Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF

Mà $EF//AC$ (chứng minh trên) và $EH//BD;EH={\displaystyle \frac{1}{2}}BD$ (do EH là đường trung bình của tam giác ABD)

Do đó $EH\perp EF\iff AC\perp BD$

Vậy tứ giác EFGH là hình chữ nhật thì $AC\perp BD$

b. Hình bình hành EFGH là hình thoi ⇔ EH = EF

Mà EF = ${\displaystyle \frac{1}{2}}$AC (chứng minh trên) và $EH={\displaystyle \frac{1}{2}}BD$ (chứng minh trên)

Nên $EH=EF\iff AC=BD$ 

Vậy tứ giác EFGH là hình thoi thì $AC=BD$

c. Tứ giác EFGH là hình vuông khi EFGH vừa là hình thoi, vừa là hình chữ nhật.

Từ câu a, b suy ra tứ giác EFGH là hình vuông $\iff AC\perp BD$ và $AC=BD$

Bài 158 Trang 100 SBT Toán 8 Tập 1 Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.

a. Tứ giác AEDF là hình gì ? Vì sao ?

b. Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?

c. Chứng minh rằng M đối xứng với N qua A

d. Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?

Phương pháp giải:

Vận dụng kiến thức :

- Tứ giác có ba góc vuông là hình chữ nhật.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

- Tính chất về các cạnh và góc của hình thoi; hình vuông.

Lời giải:

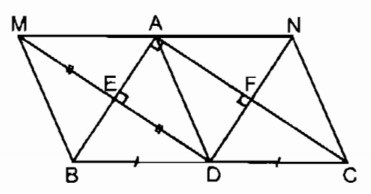
a. Điểm M và điểm D đối xứng qua trục AB

⇒ AB là đường trung trực của đoạn thẳng MD

⇒ AB ⊥ DM

⇒ $\widehat{AED}={90}^0$

Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN

⇒ AC ⊥ DN $\Rightarrow \widehat{AFD}={90}^0$

Mà $\widehat{EAF}={90}^0$ (gt)

Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)

b. Tứ giác AEDF là hình chữ nhật

⇒ DE // AC; DF // AB

Trong ∆ ABC ta có: DB = DC (gt)

Mà DE // AC

Suy ra: AE = EB (tính chất đường trung bình tam giác)

Lại có DF// AB và DB=DC

Suy ra: AF = FC (tính chất đường trung bình của tam giác)

Xét tứ giác ADBM : AE = EB (chứng minh trên)

ED = EM (vì AB là trung trực của DM)

Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Mặt khác: AB ⊥ DM

Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)

Xét tứ giác ADCN:

AF = FC (chứng minh trên)

DF = FN (vì AC là đường trung trực của DN)

Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Mà AC ⊥ DN

Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)

c. Tứ giác ADBM là hình thoi

⇒ AM // DB và AM = AD (tính chất) 

Hay AM // BC và AM = AD (1)

Tứ giác ADCN là hình thoi

⇒ AN // DC và AD = AN (tính chất)

Hay AN // BC và AN = AD (2)

Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng

Và AM = AN nên A là trung điểm của MN

Vậy điểm M và điểm N đối xứng với nhau qua điểm A

d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF

Ta có: AE = ${\displaystyle \frac{1}{2}}$AB ; AF =${\displaystyle \frac{1}{2}}$AC

Nên AE = AF ⇒ AB = AC

Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

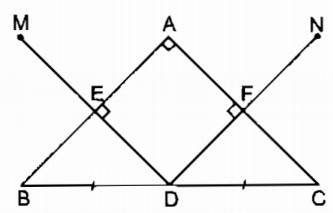
Bài 159 Trang 100 SBT Toán 8 Tập 1 Cho tam giác ABC vuông tại A, đường cao AH. Gọi 

b. Tam giác DHE là tam giác gì ? Vì sao ?

c. Tứ giác BDEC là hình gì ? Vì sao ?

d. Chứng minh rằng BC = BD + CE.

Phương pháp giải:

Nhẩm lại dấu hiệu nhận biết của các tứ giác đã học rồi chứng minh.

Hình thang có 1 góc vuông là hình thang vuông

Trong một tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông

Lời giải:

a) Điểm D đối xứng điểm H qua trục AB

⇒ AB là đường trung trực của HD 

⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A

Suy ra: AB là tia phân giác của $\widehat{DAH}\Rightarrow \widehat{DAB}={\hat{A}}_1$

Điểm H và điểm E đối xứng qua trục AC

⇒ AC là đường trung trực của HE

⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A

Suy ra: AC là đường phân giác của $\widehat{HAE}\Rightarrow {\hat{A}}_2=\widehat{EAC}$

Ta có: $\widehat{DAE}=\widehat{DAH}+\widehat{HAE}$$=2\left({\hat{A}}_1+{\hat{A}}_2\right)={2.90}^0={180}^0$

Suy ra D, A, E thẳng hàng

Lại có: AD = AE (vì cùng bằng AH)

Nên điểm A là trung điểm của đoạn DE

Vậy điểm D đối xứng với điểm E qua điểm A.

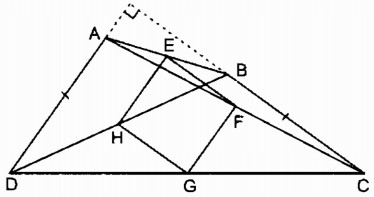
Bài 160 Trang 100 SBT Toán 8 Tập 1 Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

b. Hình thoi

c. Hình vuông

Phương pháp giải:

- Vận dụng kiến thức : Tứ giác có hai cặp cạnh đối song song và bằng nhau là hình bình hành.

- Nhẩm lại dấu hiệu nhận biết của hình chữ nhật, hình thoi, hình vuông có liên quan đến hình bình hành và tìm lời giải cho bài toán.

Lời giải:

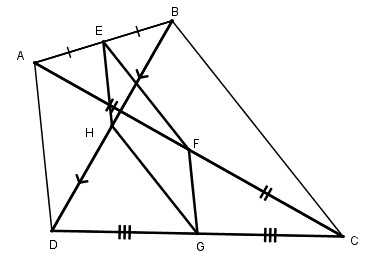
Xét tam giác ABC: 

Ta có: EB = EA, FA = FC (gt)

Nên EF là đường trung bình của tam giác ABC

Suy ra EF // BC, EF = ${\displaystyle \frac{1}{2}}$  BC (tính chất)

Xét tam giác BDC có: 

HB = HD, GD = GC (gt)

Nên HG là đường trung bình của tam giác BDC

Suy ra HG // BC, HG =  ${\displaystyle \frac{1}{2}}$  BC (tính chất) 

Do đó EF //HG, EF = HG.

Vậy EFGH là hình bình hành.

Xét tam giác ABD: 

Ta có: EB = EA, HB = HD (gt)

Nên EH là đường trung bình của tam giác ABD

Suy ra EH // AD, EH = ${\displaystyle \frac{1}{2}AD}$ (tính chất)

a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF

Mà EF // BC và EH//AD (chứng minh trên)

Do đó $EH\perp EF\iff AD\perp BC$

Hay để EFGH là hình chữ nhật thì $AD\perp BC$

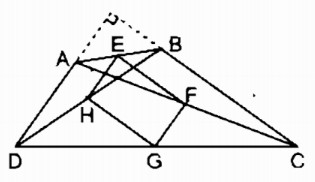
b) Hình bình hành EFGH là hình thoi ⇔ EH = EF

Mà EH = ${\displaystyle \frac{1}{2}AD}$ và EF = ${\displaystyle \frac{1}{2}}$  BC (chứng minh trên)

Nên $EH=EF\iff AD=BC$

Vậy EFGH là hình thoi ⇔ AD = BC. 

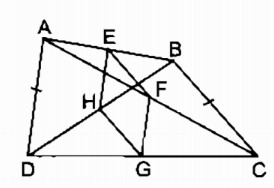
c)  EFGH là hình vuông khi EFGH vừa là hình thoi, vừa là hình chữ nhật

Từ câu a, b ta có EFGH là hình vuông ⇔ AD ⊥ BC và AD = BC

Bài 161 Trang 100 SBT Toán 8 Tập 1 Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC.

a. Chứng minh rằng tứ giác DEHK là hình bình hành.

b. Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật ?

c. Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì ?

Phương pháp giải:

Vận dụng kiến thức :

- Tính chất ba đường trung tuyến trong tam giác.

- Dấu hiệu nhận biết hình bình hành, hình chữ nhật và hình thoi.

Lời giải:

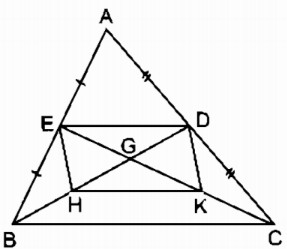
a. Tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.

Ta có: GD = ${\displaystyle \frac{1}{2}}$GB (tính chất đường trung tuyến của tam giác)

GH = ${\displaystyle \frac{1}{2}}$GB (gt)

Suy ra: GD = GH

GE = ${\displaystyle \frac{1}{2}}$GC (tính chất đường trung tuyến của tam giác)

GK = ${\displaystyle \frac{1}{2}}$GC (gt) 

Suy ra: GE = GK

Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

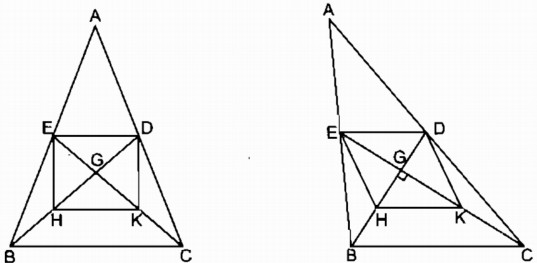
b. Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK

Mà DH = ${\displaystyle \frac{2}{3}}$BD; EK = ${\displaystyle \frac{2}{3}}$CE (tính chất đường trung tuyến của tam giác)

Nên DH = EK ⇒ BD = CE ⇒ ∆ ABC cân tại A (tam giác có 2 đường trung tuyến bằng nhau là tam giác cân)

Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.

c. Nếu BD ⊥ CE ⇒ DH ⊥ EK

Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.

Bài 162 Trang 100 SBT Toán 8 Tập 1 Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.

a. Các tứ giác AEFD, AECF là hình gì ? Vì sao ?

b. Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.

c. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông ?

Phương pháp giải:

Vận dụng kiến thức về dấu hiệu nhận biết hình bình hành, hình thoi và hình chữ nhật.

Sử dụng tính chất các cạnh, góc và đường chéo của các hình đó.

Lời giải:

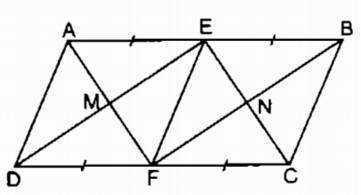
a. Xét tứ giác AEFD:

AB // CD (gt) hay AE // FD

AE = ${\displaystyle \frac{1}{2}}$AB (gt)

FD = ${\displaystyle \frac{1}{2}}$CD (gt)

Mà AB=CD (do ABCD là hình bình hành)

Suy ra: AE = FD

Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Lại có AD = AE = ${\displaystyle \frac{1}{2}}$AB

Vậy tứ giác AEFD là hình thoi.

Xét tứ giác AECF : AE // CF (gt)

AE = ${\displaystyle \frac{1}{2}}$AB (gt)

CF = ${\displaystyle \frac{1}{2}}$CD (gt)

Mà AB=CD (do ABCD là hình bình hành)

Suy ra: AE = CF

Tứ giác AECF là hình bình hành (vì có một cặp canh đối song song và bằng nhau)

b. Tứ giác AECF là hình thoi

⇒ AF ⊥ ED ⇒ $\widehat{EMF}={90}^0$

Mà AF // CE (vì tứ giác AECF là hình bình hành)

Suy ra: CE ⊥ ED $\Rightarrow \widehat{MEN}={90}^0$

Xét tứ giác EBFD ta có: EB = FD (vì cùng bằng AE) và EB // FD (vì AB // CD)

Xét tứ giác EBFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE // BF

Suy ra: $BF\perp AF\Rightarrow \widehat{MFN}=90°$

Vậy tứ giác EMFN là hình chữ nhật (vì có 3 góc vuông)

c. 

Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF

ME = ${\displaystyle \frac{1}{2}}$DE (tính chất hình thoi AEFD)

MF = ${\displaystyle \frac{1}{2}}$AF (tính chất hình thoi AEFD)

Suy ra: DE = AF

⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)

⇒ $\hat{A}={90}^0$  ⇒ Hình bình hành ABCD là hình chữ nhật

Ngược lại: ABCD là hình chữ nhật ⇒$\hat{A}={90}^0$

Hình thoi AEFD có $\hat{A}={90}^0$ nên AEFD là hình vuông

⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)

Hình chữ nhật EMFN là hình vuông (vì có hai cạnh kề bằng nhau)

Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.

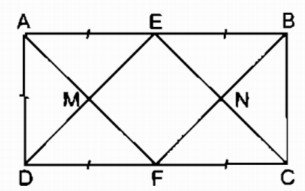
Bài 163 Trang 100 SBT Toán 8 Tập 1 Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.

a. Tứ giác DEBF là hình gì ? Vì sao ?

b. Chứng minh rằng các đường thẳng AC, BD, EF cùng cắt nhau tại một điểm.

c. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.

Phương pháp giải:

- Dấu hiệu nhận biết hình bình hành: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành

- Tính chất về các cạnh và đường chéo của hình bình hành.

Lời giải:

a) Xét tứ giác DEBF: AB // CD (vì ABCD là hình bình hành) hay DF // EB

EB = ${\displaystyle \frac{1}{2}}$AB (do E là trung điểm của AB)

DF = ${\displaystyle \frac{1}{2}}$CD (do F là trung điểm của DC)

Mà AB=CD (do ABCD là hình bình hành)

Suy ra: EB = DF

Vậy tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

b) Gọi O là giao điểm của AC và BD

OB = OD (tính chất hình bình hành ABCD)

Vì tứ giác DEBF là hình bình hành nên EF và BD cắt nhau tại trung điểm của mỗi đường

Suy ra: EF đi qua trung điểm O của BD

Vậy AC, BD và EF cắt nhau tại O trung điểm của mỗi đoạn

c. Vì DEBF là hình bình hành nên DE//BF

Suy ra $\widehat{MEO}=\widehat{NFO}$ (so le trong)

Xét ∆ EOM và ∆ FON:

$\widehat{MEO}=\widehat{NFO}$ (chứng minh trên)

OE = OF (tính chất hình bình hành DEBF)

$\widehat{MOE}=\widehat{NOF}$  (đối đỉnh)

Do đó : $∆EOM=∆FON(g.c.g)$$\Rightarrow OM=ON$

Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Bài 164 Trang 101 SBT Toán 8 Tập 1 Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD.

a. Tính khoảng cách từ I đến AB

b. Khi điểm M di chuyển trên đoạn thẳng AB thì điểm I di chuyển trên đường nào ?

Phương pháp giải:

- Vận dụng tính chất của tam giác cân và tính chất về giao điểm hai đường chéo của hình vuông.

- Xác định khoảng cách giữa I với đoạn thẳng AB.

Lời giải:

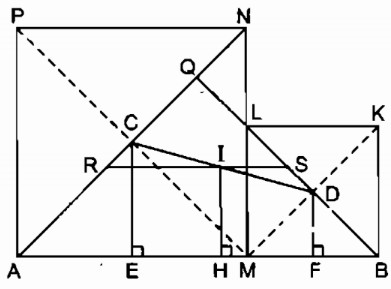
a. Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB 

⇒ CE // DF // IH (cùng vuông với AB)

Suy ra DCEF là hình thang.

Xét hình thang DCEF có: 

CE // DF // IH và IC = ID (vì I là trung điểm của CD)

Nên H là trung điểm cạnh EF

Suy ra IH là đường trung bình của hình thang DCEF

$\Rightarrow IH={\displaystyle \frac{DF+CE}{2}}$ (1)

Vì C là tâm hình vuông AMNP nên $CA=CM$ (tính chất) và $\widehat{ACM}={90}^0$

⇒ ∆ CAM là tam giác vuông cân tại C

Lại có CE ⊥ AM hay CE là đường cao của tam giác cân CAM

⇒ CE cũng là đường trung tuyến (tính chất tam giác cân)

⇒ CE = ${\displaystyle \frac{1}{2}}$AM (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Vì D là tâm hình vuông BMLK nên $DB=DM$ (tính chất) và $\widehat{MDB}={90}^0$

⇒ ∆ DBM vuông cân tại D

Có DF ⊥ BM nên DF là đường cao của tam giác cân DBM

⇒ DF cũng là đường trung tuyến (tính chất tam giác cân)

⇒ DF = ${\displaystyle \frac{1}{2}}$BM (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Vậy CE + DF = ${\displaystyle \frac{1}{2}}$AM + ${\displaystyle \frac{1}{2}}$BM

= ${\displaystyle \frac{1}{2}}$ (AM + BM) = ${\displaystyle \frac{1}{2}}$AB = ${\displaystyle \frac{a}{2}}$

Từ (1) ta suy ra: 

$\Rightarrow IH={\displaystyle \frac{DF+CE}{2}}$ $={\displaystyle \frac{{\displaystyle \frac{a}{2}}}{2}=\frac{a}{4}}$

b. Gọi Q là giao điểm của BL và AN

Ta có: AN ⊥ MP (2) (tính chất hình vuông APNM)

BL ⊥ MK (3) (tính chất hình vuông BMLK)

Lại có: $\widehat{PMN}={\displaystyle \frac{1}{2}}\widehat{AMN}={\displaystyle \frac{1}{2}}{.90}^0={45}^0$ (do APNM là hình vuông nên MP là phân giác góc AMN) 

$\widehat{KMN}={\displaystyle \frac{1}{2}}\widehat{BML}={\displaystyle \frac{1}{2}}{.90}^0={45}^0$ (do BMLK là hình vuông nên MK là phân giác góc BML) 

$\Rightarrow \widehat{PMK}=\widehat{PMN}+\widehat{NMK}$$={45}^0+{45}^0={90}^0$

Suy ra MP ⊥ MK (4)

Từ (2), (3) và (4) suy ra BL ⊥ AN

Lại có $\widehat{QAB}={\displaystyle \frac{1}{2}}\widehat{MAP}$$={\displaystyle \frac{1}{2}}{.90}^0={45}^0$ (do APNM là hình vuông)

⇒ ∆ QAB vuông cân tại Q cố định. 

Khi M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng ${\displaystyle \frac{a}{4}}$  nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng ${\displaystyle \frac{a}{4}}$

Khi M trùng B thì I trùng với S là trung điểm của BQ 

Khi M trùng với A thì I trùng với R là trung điểm của AQ

Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng ${\displaystyle \frac{a}{4}}$ .

Bài 1.1 Trang 101 SBT Toán 8 Tập 1 Điền vào chỗ trống :

a. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là .....

b. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là ....

c. Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là .....

Phương pháp giải:

Nhẩm lại dấu hiệu nhận biết của các hình rồi điền từ thích hợp vào chỗ trống.

Lời giải:

Điền vào chỗ trống lần lượt là

a. hình bình hành

b. hình chữ nhật

c. hình thoi.

Bài 1.2 Trang 101 SBT Toán 8 Tập 1 Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC.

a. Chứng minh rằng ADEF là hình thoi

b. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?

Phương pháp giải:

Vận dụng kiến thức về dấu hiệu nhận biết và tính chất của hình thoi; dấu hiệu nhận biết hình vuông.

Tứ giác có 4 cạnh bằng nhau là hình thoi

Hình thoi có 1 góc vuông là hình vuông

Lời giải:

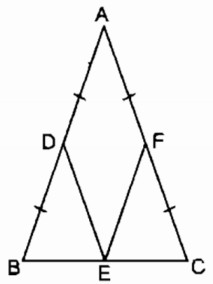
a. Ta có: E là trung điểm của BC (gt)

D là trung điểm của AB (gt)

nên ED là đường trung bình của ∆ ABC

Suy ra DE = AF = ${\displaystyle \frac{1}{2}}$AC (1)

Lại có: 

E là trung điểm của BC (gt)

F là trung điểm của AC (gt)

nên EF là đường trung bình ∆ ABC

⇒ EF = AD = ${\displaystyle \frac{1}{2}}$AB (2)

Mà AB = AC (3) (do tam giác ABC cân tại A)

Từ (1), (2) và (3) suy ra: AD = DE = EF = AF

Vậy tứ giác ADEF là hình thoi.

b. Hình thoi ADEF là hình vuông ⇒ $\hat{A}={90}^0$

⇒ ∆ ABC vuông cân tại A

Ngược lại nếu ∆ ABC vuông cân tại A

⇒ Tứ giác ADEF là hình thoi có $\hat{A}={90}^0$

⇒ Hình thoi ADEF là hình vuông

Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.