Toptailieu.vn biên soạn và giới thiệu lời giải Chuyên đề Tin học 11 (Kết nối tri thức) Bài 1: Đệ quy và hàm đệ quy hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi từ đó học tốt môn Chuyên đề Tin học 11.

Chuyên đề Tin học 11 (Kết nối tri thức) Bài 1: Đệ quy và hàm đệ quy

Khởi động trang 5 Chuyên đề Tin học 11: Trong cuộc sống hằng ngày, các em thường gặp các hiện tượng, sự vật, sự việc thể hiện giống hệt nhau, được lặp đi lặp lại với quy mô khác nhau. Ví dụ, búp bê Matryoshka rất nổi tiếng của Nga, khi mở búp bê mẹ ra chúng ta lại thấy búp bê con bên trong. Cây súp lơ có mỗi nhánh của cây súp lơ là hình ảnh thu nhỏ của cả cây súp lơ, …Em có thể nói gì về đặc điểm chung nhất của các búp bê Matryoshka, lá cây dương xỉ và cây súp lơ?

Lời giải:

Đặc điểm chung nhất của các búp bê Matryoshka, lá cây dương xỉ và cây súp lơ là đều được định nghĩa dựa trên chính bản thân chúng

1. Khái niệm đệ quy

Hoạt động 1 trang 5 Chuyên đề Tin học 11: Quan sát mô hình dãy số được tạo ra (Hình 1.4) và trả lời câu hỏi

Hình 1.4. Mô hình dãy số

1. Dãy số được tạo theo quy luật nào?

2. Em hãy xác định hình và dãy số trong trường hợp n = 6

Lời giải:

1. Quy luật: Số đằng sau = số đằng trước + số thứ tự của nó

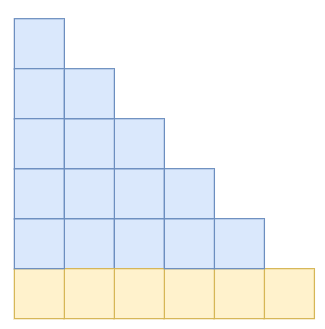
2. Với n = 6:

Hình như sau: Vẽ thêm một hàng có 6 ô ở dưới hình có n = 5

 Dãy số: f(6) = (1 + 2 + 3 + 4 + 5) + 6 = 21 = f(5) + 6

Câu hỏi 1 trang 6 Chuyên đề Tin học 11: Trường hợp nào sau đây không có tính chất đệ quy?

Lời giải:

Trường hợp D. Ngôi sao không có tính chất đệ quy vì không thể định nghĩa theo chính nó

Câu hỏi 2 trang 7 Chuyên đề Tin học 11: Phát biểu nào sau đây là sai về đệ quy

A. Một đối tượng được gọi là đệ quy nếu nó hoặc một phần của nó được định nghĩa thông qua khái niệm về chính nó.

B. Đối tượng đệ quy thì sự vật, hiện tượng liên quan đến đối tượng sẽ được lặp lại nhiều lần.

C. Trong đệ quy, lời giải của một bài toán phụ thuộc vào lời giải của các trường hợp nhỏ hơn của cùng một bài toán

D. Đệ quy là cách gọi khác của lặp.

Lời giải:

Đáp án đúng: D

Đệ quy và lặp là hai khái niệm khác nhau trong lập trình. Đệ quy là cách giải quyết một bài toán bằng cách chia nhỏ thành các bài toán con cùng loại và giải quyết chúng đệ quy cho đến khi nào đạt được điều kiện dừng. Trong khi đó, lặp là việc lặp đi lặp lại một hành động nào đó cho đến khi đạt được điều kiện dừng.

2. Công thức truy hồi

Hoạt động 2 trang 7 chuyên đề học tập Tin học 11: Đọc, quan sát các công thức sau để phát hiện các đặc điểm tương tự giữa các công thức này và khái niệm đệ quy

Lời giải:

- Tất cả các công thức truy hồi đều có hai phần: phần cơ sở để xác định các giá trị ban đầu và phần truy hồi để tính các phần tử tiếp theo.

- Đệ quy là việc tất cả các dãy số được định nghĩa thông qua công thức truy hồi

Câu hỏi trang 8 Chuyên đề Tin học 11: 1.Em hãy xác định phần cơ sở và phần đệ quy của n!

2. Em hãy xác định phần cơ sở và phần đệ quy của xⁿ

Lời giải:

1. Xác định phần cơ sở và phần đệ quy của n!:

Phần cơ sở: $P_0=\mathrm{1,}{\text{\hspace{0.17em}P}}_1=1$

Phần đệ quy: $P_n=n\times (n-1)!\text{\hspace{0.17em}neu\hspace{0.17em}n}>1$

2. Xác định phần cơ sở và phần đệ quy của: xⁿ

Phần cơ sở: $P_0=1$

Phần đệ quy: $P_n=x\times x^{n-1}\text{\hspace{0.17em}\hspace{0.17em}neu\hspace{0.17em}n}>0$

3. Hàm đệ quy

Hoạt động 3 trang 8 Chuyên đề Tin học 11 Bạn An được yêu cầu viết các hàm đệ quy cho các bài toán sau

1. Viết một hàm có chức năng in ra các số đếm ngược từ n xuống 1.

2. Viết hàm tính số Fibonacci thứ n.

Bạn An đã viết các hàm giải hai bài toán trên như sau:

Các hàm trên của bạn An có đúng không?

Lời giải:

Các hàm của bạn An đều bị lỗi:

- Hàm của chương trình 1 sẽ bị lặp vô hạn lần. Như vậy, muốn sửa lỗi này cần có các lệnh điều khiển làm dừng quá trình gọi đệ quy. Các lệnh này được gọi là lệnh điều khiển dừng hay phần điều khiển dừng của hàm. Chương trình 1 được viết lại đúng sau khi thêm phần điều khiển dừng như sau:

- Chương trình 2 có 2 lỗi: lỗi gọi đệ quy vô hạn không dừng và lỗi không thiết lập được các giá trị ban đầu của số Fibonacci với các trường hợp n = 0 và n = 1. Như vậy, để sửa các lỗi này cần đưa vào các lệnh điều khiển dừng gọi đệ quy vô hạn và các lệnh thiết lập các giá trị ban đầu của dãy. Các lệnh thiết lập các giá trị ban đầu của hàm với tham số đầu vào nhỏ sẽ được gọi là phần cơ sở của hàm đệ quy.

Câu hỏi 1 trang 10 Chuyên đề Tin học 11: Trong chương trình tính số Fibonacci, các lệnh nào là phần cơ sở, các lệnh nào là phần đệ quy của chương trình?

Lời giải:

Xác định phần cơ sở và phần đệ quy của chương trình tính số Fibonacci:

Phần cơ sở: $F_0=\mathrm{0,}{\text{\hspace{0.17em}\hspace{0.17em}F}}_1=1$

Phần đệ quy: $F_n={\text{\hspace{0.17em}F}}_{n-1}+F_{n-2}\text{\hspace{0.17em}neu\hspace{0.17em}n}>1$

Câu hỏi 2 trang 10 Chuyên đề Tin học 11: Một hàm đệ quy sẽ có những thành phần nào?

A. Phần cơ sở và phần khởi tạo.

B. Phần cơ sở và phần đệ quy.

C. Phần đệ quy và phần khởi tạo.

Lời giải:

Đáp án đúng: B

Một hàm đệ quy có hai phần: phần cơ sở để xác định các giá trị ban đầu và phần đệ quy để tính các phần tử tiếp theo.

Luyện tập

Luyện tập 1 trang 10 Chuyên đề Tin học 11: Viết chương trình in và đếm xuôi từ 1 đến 100 trên màn hình

Lời giải:

Chương trình đệ quy Python để in và đếm từ 1 đến 100 trên màn hình có thể được viết như sau. Trong đó, hàm count được định nghĩa để in số và gọi lại chính nó với giá trị đầu vào tăng lên 1. Nếu giá trị đầu vào là 100 hoặc lớn hơn, hàm sẽ kết thúc đệ quy.

Chạy chương trình sẽ cho kết quả in ra các số từ 1 đến 100 trên màn hình.

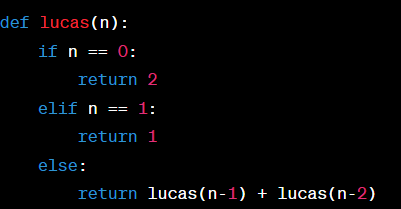
Luyện tập 2 trang 10 Chuyên đề Tin học 11: Viết chương trình tính số Lucas thứ n

Lời giải:

Xác định phần cơ sở và phần đệ quy của chương trình tính số Fibonacci:

Phần cơ sở: $L_0=\mathrm{2,}{\text{\hspace{0.17em}L}}_1=1$

Phần đệ quy: $L_n={\text{\hspace{0.17em}\hspace{0.17em}L}}_{n-1}+L_{n-2}\text{\hspace{0.17em}neu\hspace{0.17em}n}>1$

Chương trình viết như sau

Vận dụng

Vận dụng 1 trang 10 Chuyên đề Tin học 11: Viết chương trình nhập số n từ bàn phím và in ra n số hạng đầu tiên của dãy số Peil

Lời giải:

Chương trình nhập số n từ bàn phím và in ra n số hạng đầu tiên của dãy số Peil:

Vận dụng 2 trang 10 Chuyên đề Tin học 11: Viết chương trình tính số Peil thứ n 

Lời giải:

Chương trình tính số Peil thứ n:

Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 2: Thiết kế thuật toán đệ quy

Bài 3: Thực hành giải toán theo kĩ thuật đệ quy

Bài 4: Tháp Hà Nội

Bài 5: Thực hành thiết kế thuật toán theo kĩ thuật đệ quy

Bài 6: Ý tưởng và kĩ thuật chia để trị