Toptailieu.vn xin giới thiệu 27 câu trắc nghiệm Ôn tập chương 3 (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

27 câu trắc nghiệm Ôn tập chương 3 (có đáp án) chọn lọc

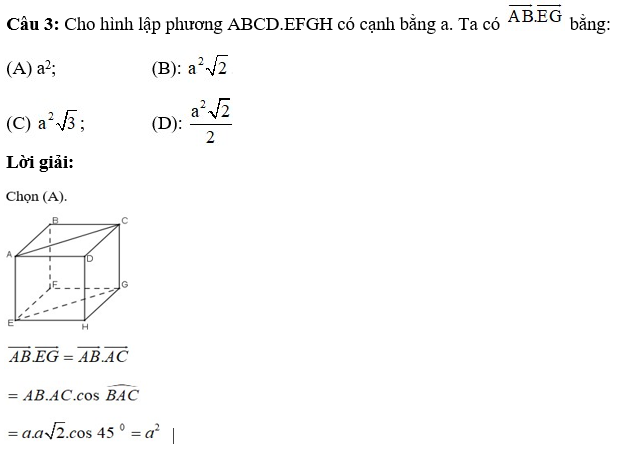
Câu 4: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

(A)          Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c.

(B)           Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c.

(C)           Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c.

(D)          Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a,b)

Lời giải:

Chọn B.

Vì đường thẳng a vuông góc với đường thẳng b nên (a, b) = 90°.

Mà b // c nên (a; c) = (a; b) = 90°

Do đó, đường thẳng a vuông góc với đường thẳng c.

Câu 5: Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng

(A)          Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.

(B)           Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.

(C)           Hai mặt phẳng (α) và (β) vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc (α) và mỗi điểm B thuộc (β) thì ta có đường thẳng AB vuông góc với d.

(D)          Nếu hai mặt phẳng (α) và (β) đều vuông góc với mặt phẳng (γ) thì giao tuyến d của (α) và (β) nếu có sẽ vuông góc với (γ)

Lời giải:

Chọn D.

(A)   Sai, vì mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vẫn có thể cắt nhau. Khi đó giao tuyến của chúng sẽ vuông góc với mặt phẳng thứ ba.

(B)   Hai mặt phẳng này vuông góc với nhau thì chỉ có những đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến thì mới vuông góc với mặt phẳng kia.

Vậy (B) sai.

(C)   sai

(D)   Đúng (Định lí 2 trang 109 SGK)

Câu 6: Tìm mệnh đề sai trong các mệnh đề sau:

(A)          Hai đường thẳng a và b trong không gian có các vector chỉ phương lần lượt là vector u và vector v. Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vector u và vector v không cùng phương.

(B)           Cho a, b là hai đường thẳng chéo nhau và vuông góc với nhau. Đường vuông góc chung của a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.

(C)           Không thể có một hình chóp tứ giác S.ABCD nào có hai mặt bên (SAB) và (SCD) cùng vuông góc với mặt phẳng đáy.

(D)          Cho vector u và vector v là hai vector chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng (α) và vector n là vector chỉ phương của đường thăng Δ. Điều kiện cần và đủ để Δ  (α) là vector n nhân vector u bằng 0 và vector n nhân vector v bằng 0.

Lời giải:

Chọn C.

+) Mệnh đề (A) đúng.

Vì hai vecto chỉ phương u→; v→ không cùng phương với nhau nên suy ra hai đường thẳng a và b không song song, không trùng nhau (1).

Vì a và b không có điểm chung nên hai đường thẳng này không cắt nhau. (2) Từ (1) và (2) suy ra, hai đường thẳng a và b ở vị trí chéo nhau.

+) Mệnh đề (B) đúng.

Giả sử đường vuông góc chung của a và b là c và a  b .

Câu 7: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

(A)  Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.

(B)   Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.

(C)   Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng.

(D)  Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy.

Lời giải:

Chọn D.

(A)   Sai vì có thể xảy ra trường hợp ba đường thẳng đồng quy nhưng không đồng phẳng.

(B)   Sai vì nếu đường thẳng thứ ba đi qua giao điểm của hai đường thẳng đã cho thì xảy ra trường hợp cả ba đường thẳng không cùng nằm trong một mặt phẳng.

(C)   Sai vì có thể xảy ra trường hợp đồng quy nhưng không đồng phẳng.

(D)   Đúng.

Câu 8: Trong các mệnh đề sau , mệnh đề nào là đúng?

(A)   Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

(B)   Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.

(C)   Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.

(D)   Hai đường thẳng không cắt nhau và không song song thì chéo nhau.

Lời giải:

Chọn A.

(A)   Đúng

(B)   Sai – Vì hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vẫn có thể cắt nhau.

(C)   Sai - Chúng có thể cắt nhau hoặc chéo nhau.

(D)   Sai - Chúng có thể trùng nhau.

Câu 9: Trong các mệnh đề sau, mệnh đề nào là đúng?

(A)   Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì chéo nhau.

(B)   Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.

(C)   Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.

(D)   Một mặt phẳng (α) và một đường thẳng a không thuộc (α) cùng vuông góc với đường thẳng b thì (α) song song với a.

Lời giải:

Chọn D.

(A)   sai vì chúng có thể cùng nằm tronng mặt phẳng song song với mặt phẳng đã cho và cắt nhau. Hoặc chúng có thể chéo nhau.

(B)   sai vì chúng có thể song song với nhau.

(C)   sai vì chúng có thể cùng nằm trong mặt phẳng vuông góc với đường thẳng đã cho nên có thể song song hoặc cắt nhau.

(D)   đúng

Câu 10: Tìm mệnh đề đúng trong các mệnh đề sau đây.

(A)          Đoạn vuông góc chung của hai đường thẳng kéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại.

(B)           Qua một điểm cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

(C)           Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước.

(D)          Cho ba đường thẳng a, b, c chéo nhau từng đôi một. Khi đó ba đường thẳng này sẽ nằm trong ba mặt phẳng song song với nhau từng đôi một.

Lời giải:

Chọn A.

(A)   Đúng.

(B)   Sai. Vì qua một điểm cho trước ta có thể dựng vô số mặt phẳng vuông góc với một mặt phẳng cho trước.

(C)   Sai. Qua một điểm cho trước có thể kẻ vô số đường thẳng vuông góc với đường thẳng a cho trước. Các đường thẳng này nằm trong mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng a.

(D)   Sai.

Câu 11: Khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh a bằng kết quả nào trong các kết quả sau đây?

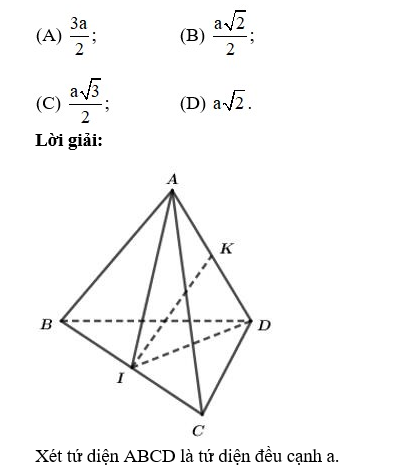
Gọi I và K lần lượt là các trung điểm của BC và AD.

Ta có: IA = ID (hai trung tuyến của hai tam giác đều bằng nhau) Nên tam giác IAD cân tại I.

Do đó IK  AD

Tương tự ta có: IK  BC.

Ta có: AI=a√2AI=a32 (đường trung tuyến trong tam giác đều)

AK=AD2=a2AK=AD2=a2

Vậy IK là đường vuông góc chung của hai cạnh đối diện AD và BC của tứ diện đều.

Tam giác AIK vuông tại K nên:

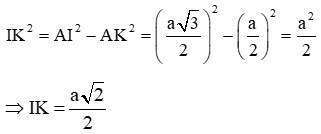
Vậy d(AD, BC) = IK = a√2a2. Chọn đáp án B

Câu 12: Trong các mệnh đề sau đây, mệnh đề nào là đúng ?

a)  Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song ;

b)  Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song ;

c)   Mặt phẳng (α) vuông góc với đường thẳng b và b vuông góc với thẳng a, thì a song song với (α).

d)  Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.

e)   Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.

Lời giải:

a)   Đúng

b)  Đúng

c)   Sai (vì a có thể nằm trong mp(α), xem hình vẽ)

d)  Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a  mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.

e)   Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P)  d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.

Câu 13: Trong các điều khẳng định sau đây, điều nào đúng?

a)                Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.

b)               Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

c)                Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.

d)               Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.

Lời giải:

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương

III).

Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.

Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.

Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

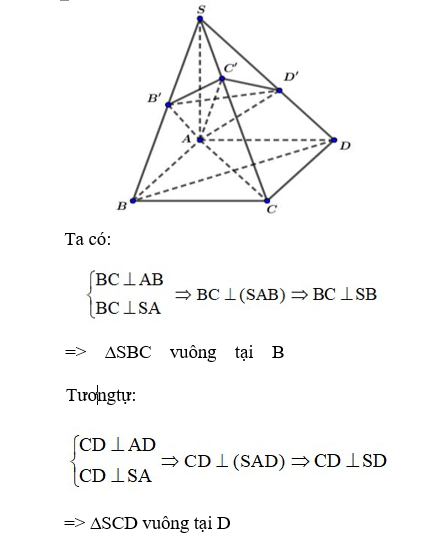
Câu 14: Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).

a)  Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.

b)  Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B^', C^', D^'. Chứng minh B^'D^' song song với BD và AB^' vuông góc với SB.

Lời giải:

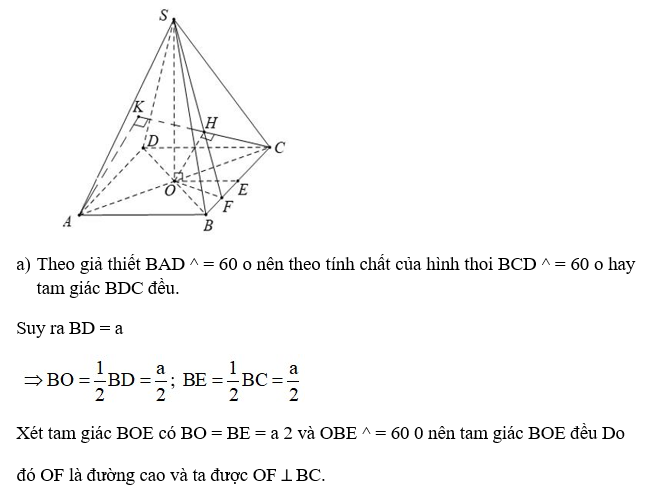
Câu 15: Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có BAD ^ = 60 o .

Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO= 3a 4 . Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE.

a)   Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).

b)  Tính các khoảng cách từ O và A đến mặt phẳng (SBC).

Lời giải:

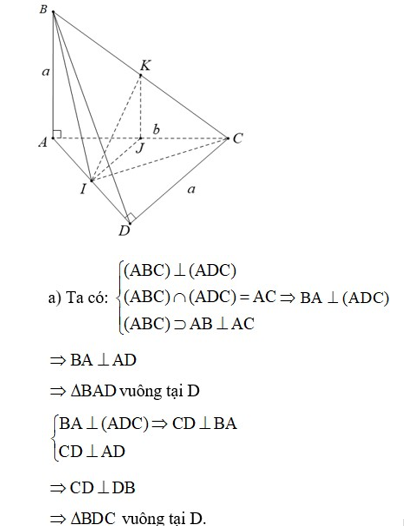
b) Gọi J là trung điểm của AC suy ra KJ // BA (đường trung bình của ∆ABC)

Mà BA  (ADC) => KJ  (ADC) => KJ  AD (1)

Ta cũng có IJ // DC (đường trung bình của ∆ADC)

Mà DC  AD => IJ  AD (2)

Từ (1) và (2) suy ra: AD  (KIJ) => AD  IK (3)

Ta lại có: ∆BAI = ∆CDI (cạnh – góc - cạnh)

Suy ra IB = IC

=> ∆BIC cân đỉnh I => IK  BC (4)

Từ (3) và (4) suy ra IK là đoạn vuông góc chung của AD và BC.

Câu 17: Cho hình lập phương ABCD.A’B’C’D’ cạnh a.

a)   Chứng minh BC’ vuông góc với mặt phẳng (A’B’CD).

b)  Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’.

Lời giải:

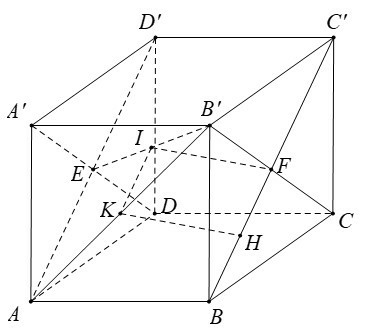
a)  Ta có tứ giác BCC’B’ là hình vuông nên BC' ⊥ B'C (1)

Mặt khác A'B' ⊥ (BCC'B') => A'B' ⊥ BC' (2)

Từ (1) và (2) suy ra: BC' ⊥ (A'B'CD).

b)  Do AD’ // BC’ nên mặt phẳng (AB’D’) là mặt phẳng chứa AB’ và song song với BC’.

Ta tìm hình chiếu của BC’ trên mặt phẳng (AB’D’)

Gọi E, F là tâm của các mặt bên ADD’A’ và BCC’B’

Từ F kẻ FI ⊥ B'E. Ta có BC’//AD’ mà BC' ⊥ (A'B'CD)

=> AD' ⊥ (A'B'CD) và IF ⊂ (A'B'CD)

AD' ⊥ IF (3)

EB' ⊥ IF (4)

Từ (3) và (4) suy ra: IF ⊥ (AB'D')

Vậy IF là hình chiếu của F trên mặt phẳng (AB’D’). Qua I ta dựng đường thẳng song song với BC’ thì đường thẳng này chính là hình chiếu của BC’ trên mặt phẳng (AB’D’)

Đường thẳng qua I song song với BC’ cắt AB’ tại K. Qua K kẻ đường thẳng song song với IF, đường này cắt BC’ tại H . KH chính là đường vuông góc chung của AB’ và BC’. Thật vậy:

Câu 18: Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là

A.  Mặt phẳng trung trực của đoạn thẳng AB

B.   Đường trung trực của đoạn thẳng AB

C.  Mặt phẳng vuông góc với AB tại A D. Đường thẳng qua A và vuông góc với AB

Lời giải:

Đáp án: A

Giải thích:

Theo định nghĩa mặt phẳng trung trực

Câu 19: Cho a, b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.

A.  Nếu a  b và b  c thì a // c

B.   Nếu a vuông góc với mặt phẳng (α) và b // (α) thì a  b

C.  Nếu a // b và b  c thì c  a

D.  Nếu a  b , b  c và a cắt c thì b vuông góc với mặt phẳng (a; c)

Lời giải:

Đáp án: A

Giải thích:

Nếu  thì a và c có thể trùng nhau nên đáp án A sai.

Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).

A.  30°               

B.   45°               

C.  60°               

D.  75°

Lời giải:

Đáp án: C

Giải thích:

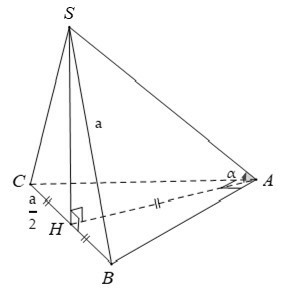
Gọi H là trung điểm của BC suy ra

AH = BH = CH = (1/2)BC = a/2

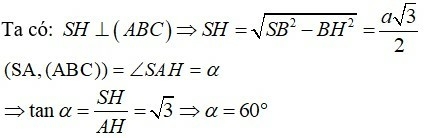
Câu 21: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)

A. 60°               

B.90°               

C.  45°                

D.  30°

Lời giải:

Đáp án: C

Giải thích:

Do H là hình chiếu của S lên mặt phẳng ( ABC) nên SH  (ABC)

Vậy AH là hình chiếu của SH lên mp(ABC)

⇒ (SA, (ABC)) = (SA, AH) = ∠ SAH

Ta có: SH ⊥ (ABC) ⇒ SH ⊥ AH

Mà: ΔABC = ΔSBC ⇒ SH = AH

Vậy tam giác SAH vuông cân tại H ⇒ SAH = 45°

Chọn C

Câu 22: Cho hình chóp S. ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:

A.  45°                  

B.   120°                   

C.  90°                  

D.  65°

Lời giải:

Đáp án: C

Giải thích:

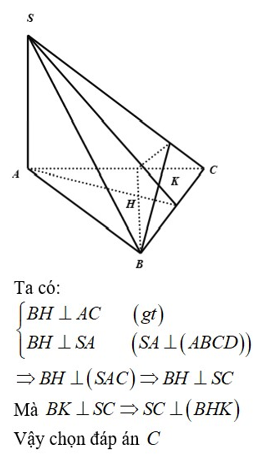
Câu 23: Cho hình hộp ABDC.A₁B₁C₁D₁. Khẳng định nào dưới đây là sai ?

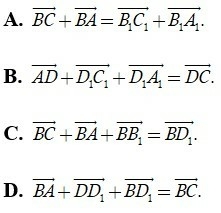
Lời giải:

Đáp án: D

Giải thích:

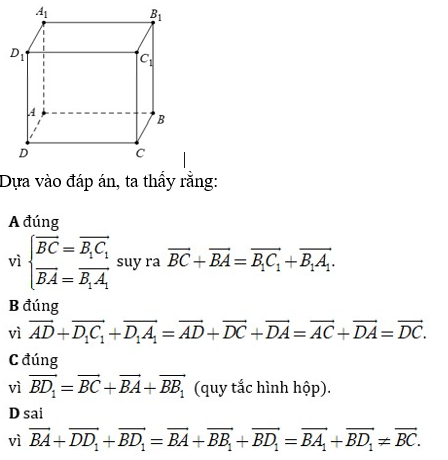
Câu 24: Cho tứ diện ABCD và I là trọng tâm tam giác ABC. Đẳng thức đúng là.

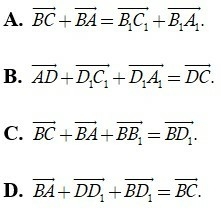
Lời giải:

Đáp án: D

Giải thích:

Vì I là trọng tâm tam giác ABC nên:

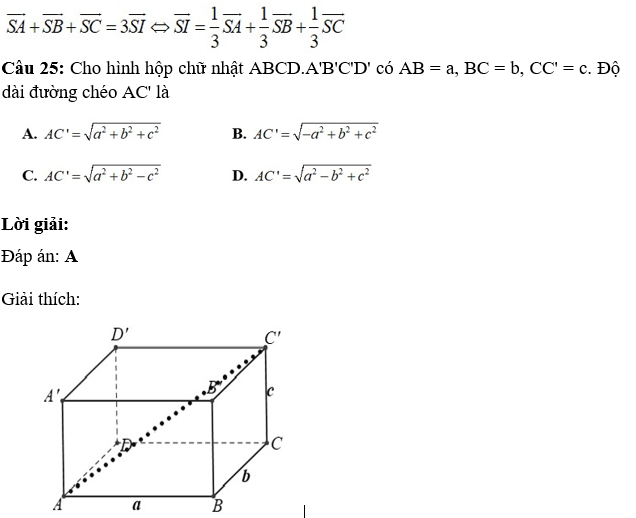
Lời giải:

Đáp án: B

Giải thích: 

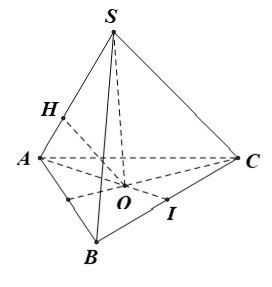
Chọn B

Vì hình chóp S.ABC đều có SO là đường cao ⇒ O là tâm của tam giác ABC.

+ Gọi I là trung điểm cạnh BC.

Lời giải:

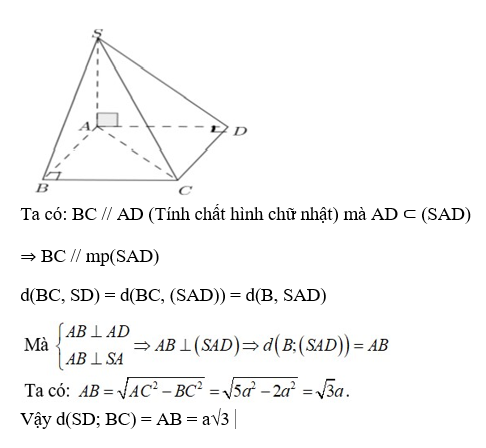
Đáp án: D

Giải thích: