Toptailieu.vn xin giới thiệu 21 câu trắc nghiệm Khoảng cách (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

21 câu trắc nghiệm Khoảng cách (có đáp án) chọn lọc

Câu 1: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a²; BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?

A. 2a              

B. 4a              

C.3a              

D. 5a

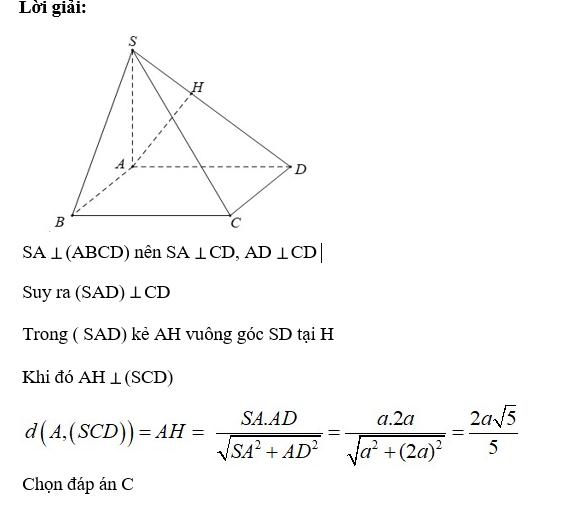
Lời giải:

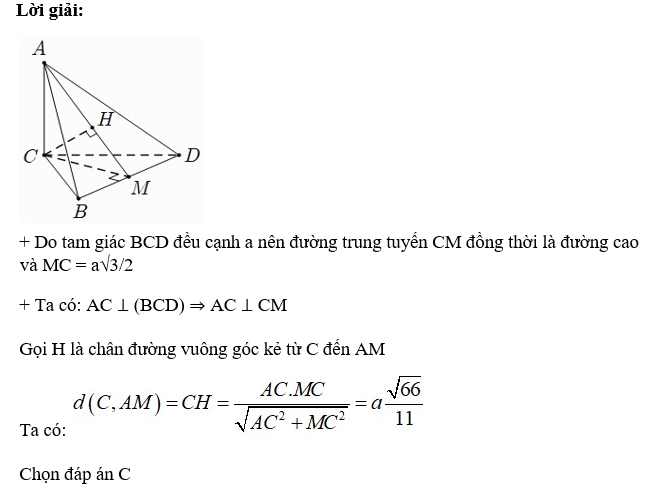
Câu 2: Cho hình chóp ABCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

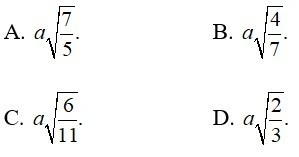
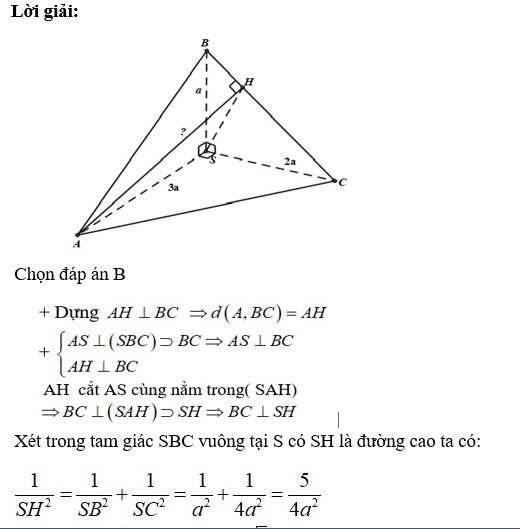
Câu 3: Cho tứ diện SABC trong đó SA; SB; SC vuông góc với nhau từng đôi một và SA = 3a; SB = a; SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

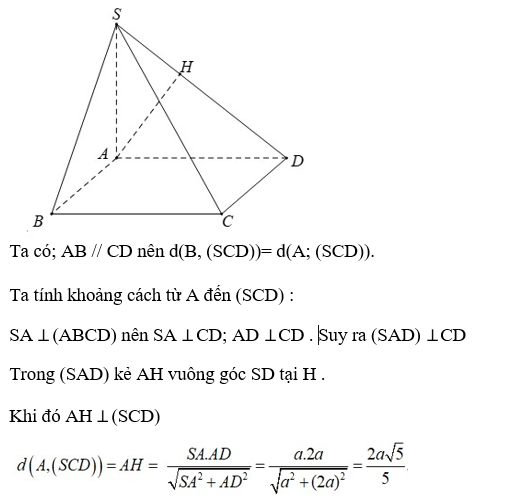
Câu 5: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a. Khoảng cách từ A đến (SCD) bằng:

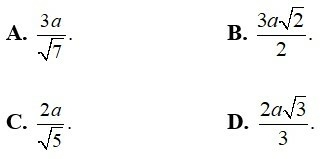
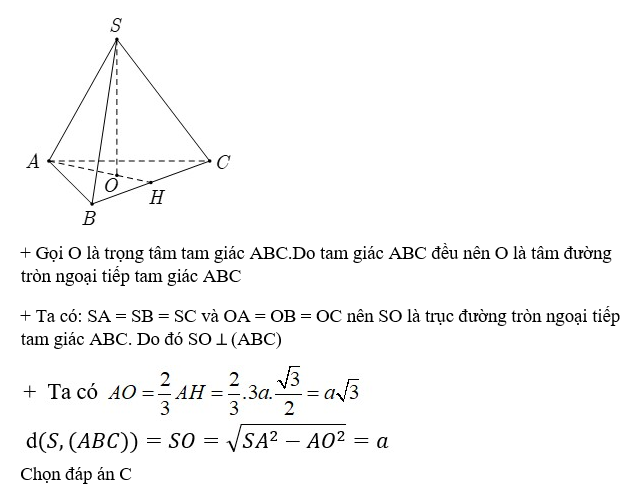
Câu 6: Hình chóp đều S.ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC) bằng :

A. 2a                

B. a√3                 

C. a                

D. a√5

Lời giải:

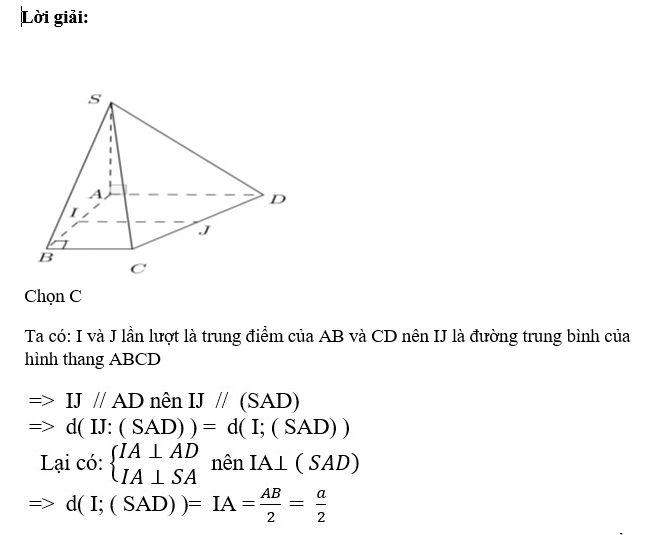
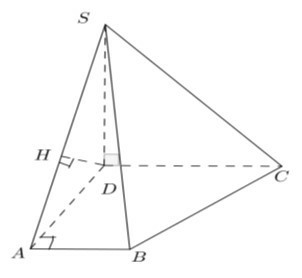
Câu 7: Cho hình chóp S. ABCD có SA  (ABCD), đáy ABCD là hình thang vuông tại A và B; AB = a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD)

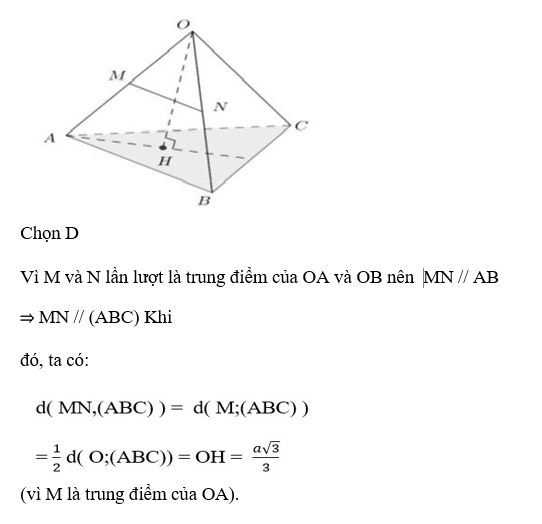
Câu 9: Cho hình chóp O.ABC có đường cao OH = 2a/√3 . Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng:

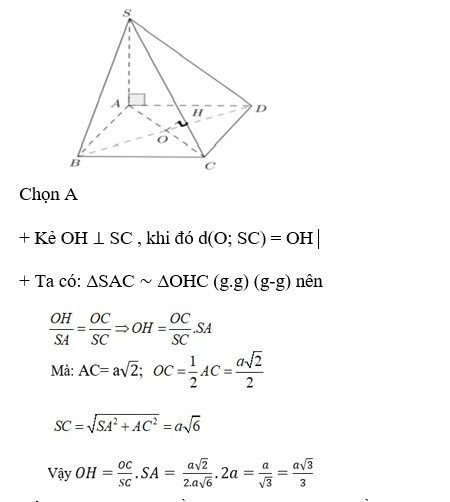
Câu 10: Cho hình chóp S. ABCD có SA ⊥ (ABCD) ; SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.

Lời giải:

Đáp án: A

Giải thích:

Câu 11: Hình chóp đều S.ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC) bằng :

A.  2a                 

B.   a√3                  

C.  a                 

D.  a√5

Lời giải:

Đáp án: C

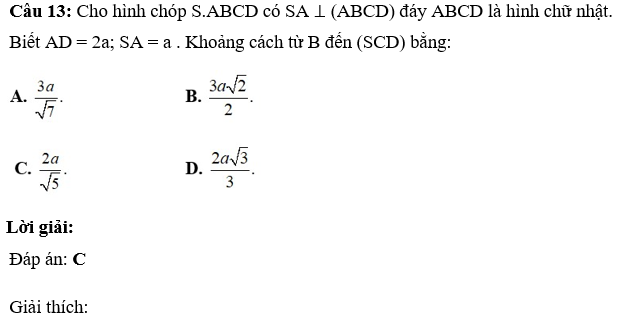
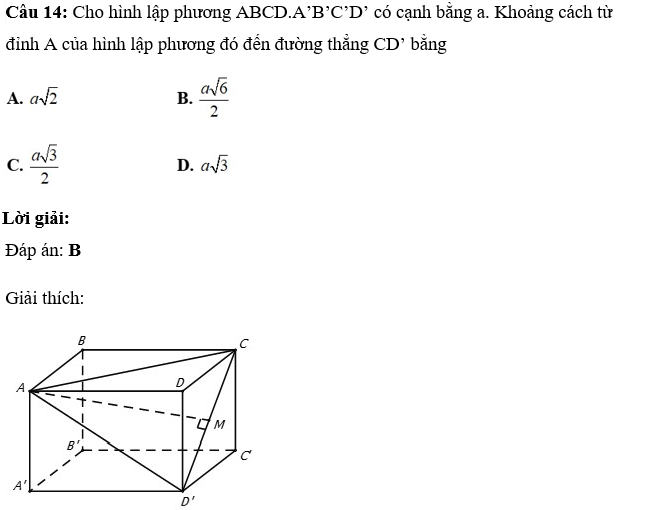
Gọi M là trung điểm của CD’

Do ABCD.A’B’C’D’ là hình lập phương nên tam giác ACD’ là tam giác đều cạnh a√2 .

+ Tam giác ACD’ có AM là đường trung tuyến nên đồng thời là đường cao AM  CD'. d(A; CD’) = AM = AC.sin(ACM) = a√2.sin60°= (a√6)/2

Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√2. Gọi

E là trung điểm AD. Khoảng cách giữa AB và (SOE) là

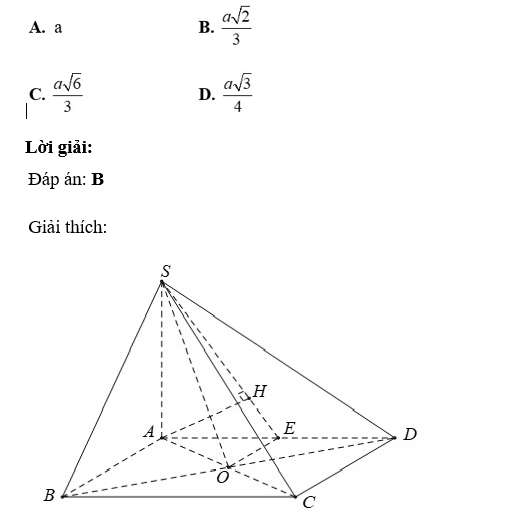
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy . mà (SAB) ∩ (SAD) = SA ⇒ SA ⊥ (ABCD) .

+ Do E là trung điểm của AD khi đó

Tam giác ABD có EO là đường trung bình

⇒ EO // AB ⇒ AB // (SOE)

⇒ d(AB, (SOE)) = d(A; (SOE)) = AH với H là hình chiếu của A lên SE.

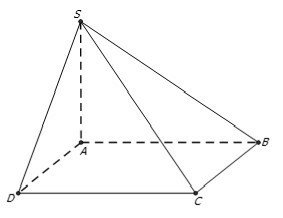
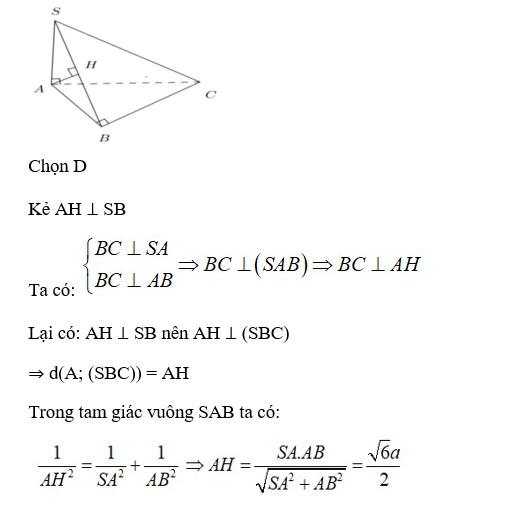
+ Ta có: BC // AD nên BC // (SAD)

⇒ d(BC; (SAD)) = d(B; SAD))

+ Ta chứng minh BA ⊥ (SAD) :

Do BA ⊥ AD (vì ABCD là hình chữ nhật)

Và BA ⊥ SA (vì SA ⊥ (ABCD))

⇒ BA ⊥ (SAD)

⇒ d(B; (SAD)) = BA

Áp dụng định lí Pytago trong tam giác vuông ABC có:

AB² = AC² - BC² = 5a² - 2a² = 3a²

⇒ AB = √3 a

⇒ d(CB; (SAD)) = AB = √3 a

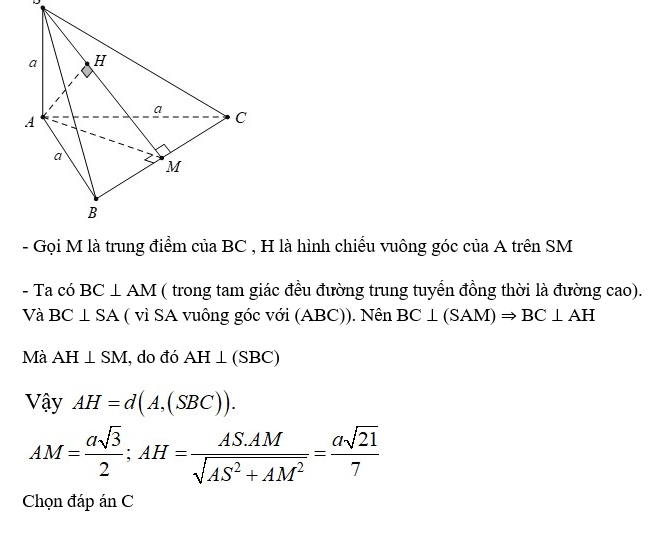
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; AB= a cạnh bên SA vuông góc với đáy và SA = a√2. Gọi M và N lần lượt là trung điểm của AB; AC. Khoảng cách giữa BC và (SMN) bằng bao nhiêu?

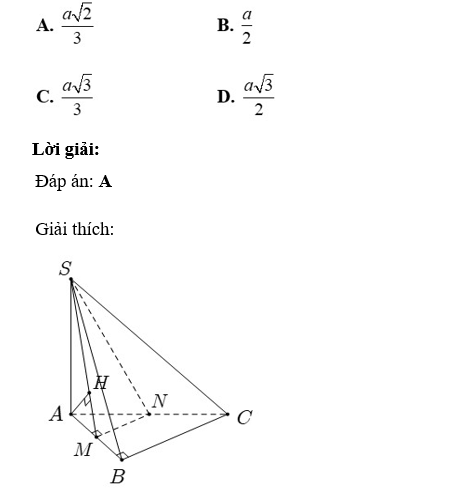
+ Tam giác ABC có MN là đường trung bình nên MN // BC ⇒ BC // (SMN) nên : d(BC; (SMN)) = d(B; (SMN)) = d(A; (SMN))

Gọi H là hình chiếu vuông góc của A trên đoạn SM.

+ Ta chứng minh: MN ⊥ (SAM):

Câu 18: Cho hình lăng trụ tam giác ABC.A’B’C’ có các cạnh bên hợp với đáy những góc bằng 60°, đáy ABC là tam giác đều và A’ cách đều A, B; C. Tính khoảng cách giữa hai đáy của hình lăng trụ.

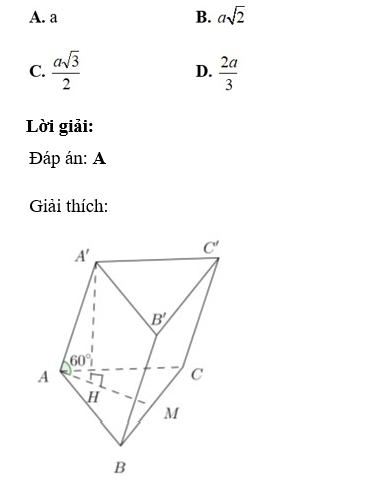
+ Vì tam giác ABC đều và AA’ = BA’ = CA’ (giả thiết) nên A’.ABC là hình chóp đều.

Gọi A’H là chiều cao của lăng trụ, suy ra H là trọng tâm tam giác ABC

Lăng trụ ABC.A’B’C’ có các cạnh bên hợp với đáy góc 60° nên A'AH = 60°.

+ Xét tam giác AHA’ có: A'H = AH.tan60° = ((a√3)/3).√3 = a

+ lại có; (ABC) // (A’B’C’) ( định nghĩa hình lăng trụ) nên d((ABC), (A’B’C’)) = d( A’, (ABC)) = A’H = a

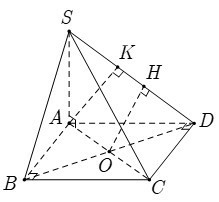
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O; SA vuông góc với đáy (ABCD). Gọi K; H theo thứ tự là hình chiếu vuông góc của A và O lên SD Chọn khẳng định đúng trong các khẳng định sau?

A.  Đoạn vuông góc chung của AC và SD là AK

B.   Đoạn vuông góc chung của AC và SD là CD

C.  Đoạn vuông góc chung của AC và SD là OH

D.  Các khẳng định trên đều sai

Lời giải:

Đáp án: D

Giải thích:

+ Ta xét các phương án:

-   Phương án A:

Giả sử AK ⊥ AC, do AK ⊥ AB ⇒ AK ⊥ (ABC)

⇒ AK ≡ SA ( vì SA ⊥ (ABC)) ⇒ SA ⊥ SD ⇒ ΔSAD có 2 góc vuông (vô lý)

-   Phương án B:

Theo tính chất của hình vuông thì AC và CD không vuông góc với nhau nên đoạn vuông góc chung của AC và SD không phải CD.

-   Phương án C:

Giả sử AC ⊥ OH, do AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SO Lại có: SA ⊥ AC ⇒ vô lý.

⇒ Đoạn vuông góc chung của AC và SD không phải là OH.

Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng?

A.              Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

B.              Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó

C.              Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia

D.              Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.

Lời giải:

Đáp án: D

Giải thích:

 Đáp án A: Đúng

 Đáp án B: Sai, do phát biểu này thiếu yếu tố cắt nhau.

 Đáp án C: Sai, vì mặt phẳng đó chưa chắc đã tồn tại.

 Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc. 

Câu 21: Trong các mệnh đề sau, mệnh đề nào sai?

A.              Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường thẳng vuông góc chung của chúng nằm trong mặt phẳng (P) chứa đường thẳng này và vuông góc với đường thẳng kia.

B.              Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm A bất kỳ thuộc a tới mp(P).

C.              Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt phẳng (P) chứa a và song song với b đến một điểm N bất kỳ trên b.

D.              Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt phẳng này đến mặt phẳng kia.

Lời giải:

Đáp an: C