Toptailieu.vn xin giới thiệu 24 câu trắc nghiệm Mặt phẳng vuông góc (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

24 câu trắc nghiệm Mặt phẳng vuông góc (có đáp án) chọn lọc

Câu 1: Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.

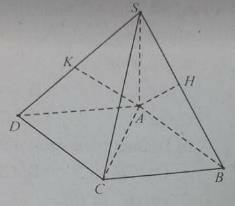
a) Hai mặt phẳng (SAB) và (SBC) vuông góc vì.

A.  Góc của (SAB) và (SBC) là góc ABC và bằng 90⁰.

B.   Góc của (SAB) và (SBC) là góc BAD và bằng 90⁰.

C.   AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)

D.  BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA

   b) Hai mặt phẳng (SAC) và (AHK) vuông góc vì:

A.              AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)

B.              AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)

C.              AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)    D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)

Lời giải:

Đáp án: a - D, b - B

a)   Phương án A sai vì AB và CB không vuông góc với giao tuyến SB của (SAB) và (SBC), nên góc ABC không phải là góc của hai mặt phẳng này; phương án B sai vì góc BAD không phải là góc của hai mặt phẳng (SAB) với mặt phẳng (SBC); phương án C sai vì AB ⊥ BC thì chưa đủ để kết luận AB vuông góc với mặt phẳng (SBC); phương án D đúng vì : BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA ⇒ (SBC) ⊥ (SAB)

b)  Phương án A sai vì hai điều kiện AH ⊥ (SBC) (do AH ⊥ SB và AH ⊥ BC) và

AK ⊥ (SCD) (do AK vuông góc với SD và AK ⊥ CD) chưa liên quan đến (SAC); phương án B đúng vì AH ⊥(SBC) và AK ⊥ (SCD) nên SC ⊥ (AHK), từ đó suy ra hai mặt phẳng (AHK) và (SAC) vuông góc; phương án C và D đều sai vì chưa đủ điều kiện kết luận SC ⊥ (AHK)

Câu 2: Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc.

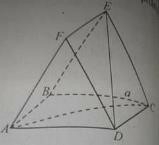
   a) DE bằng:

   A. a√3      B. a√2    C. 3a²      D. a(1 + √3)

   b) Đường thẳng DE vuông góc    A. Chỉ với AC      B. Chỉ với BF

Lời giải:

Đáp án: a - A, b - C

   EB ⊥(ABCD) vì nó vuông góc với giao tuyến AB của hai mặt phẳng vuông góc đã cho ⇒ CD ⊥ (EBC) ⇒ tam giác ECD vuông tại C.

   ⇒ DE = a√3. Vậy phương án A đúng

   Phương án C đúng vì : hình chiếu của DE lên (ABEF) là AE, mà AE ⊥ BF, suy ra DE ⊥ BF; hình chiếu của DE lên (ABCD) là BD, mà AC ⊥ BD, nên suy ra AC ⊥ DE.

Câu 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝

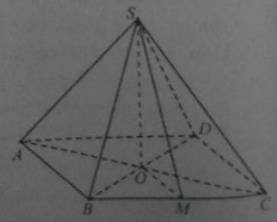
Tang của góc giữa mặt bên và mặt đáy bằng:

Lời giải:

Đáp án: C

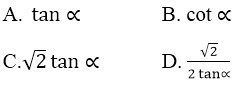
   Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)

   Ta có: BI là đường trung tuyến của tam giác ABC nên O nằm trên đường thẳng BI hay 0 ∈ BD

   Vậy SO ⊂ (SBD) và SO ⊥(ABCD) ⇒ (SBD) ⊥(ABCD)

   b) Tam giác ABD có AB = AD và góc BAD = 60⁰ nên tam giác ABD đều suy ra:

BD = a

   Ta có;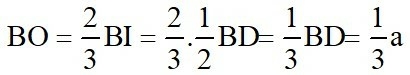

Tam giác SOB vuông tại O nên

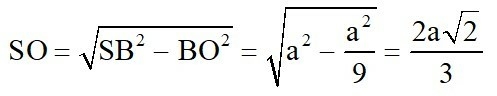
   c. Từ O vẽ OM ⊥ BC ⇒ góc OMS là góc của mặt bên và mặt phẳng đáy

   Ta có: ABCD là hình thoi nên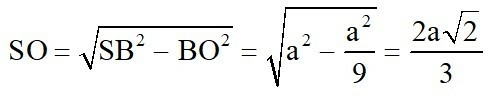 

   c) Đường vuông góc chung của AB và CD là:

   A. BN      B. AN

C. BC      D. MN

Lời giải:

Đáp án: a- B, b - C, c - D

a.   Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân

   ⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)

b.  Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)

c.   CD ⊥ MN; AB ⊥ (CDM) (do AB ⊥ CM và AB ⊥ DM)

   MN là đường vuông góc chung của AB và CD

Câu 6: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.

   a) Khằng định nào sau đây đúng?    A. AB ⊥ (ACD).

B.   BC ⊥ (ACD).

C.   CD ⊥ (ABC).

D.  AD ⊥ (BCD).

   b) Điểm cách đều bốn điểm A, B, C, D là:

A.  trung điểm J của AB

B.   trung điểm I của BC

C.   trung điểm K của AD    D. trung điểm M của CD

Lời giải:

Đáp án: a - C, b - C

a.   Phương án A sai vì chỉ có AB ⊥ CD; phương án B sai vì chỉ có : BC ⊥ CD    Phương án C đúng vì

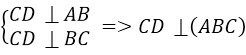
   Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng

(BCD)

a.   CD  (ABC) vì CD  AB và CD  BC

   AB  (BCD) vì AB  BC và AB  CD

   Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C

   Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C

   Phương án C đúng vì tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B và D

   Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D

Câu 7: Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.

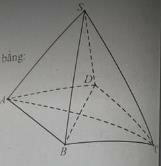
a) Đường thẳng SA vuông góc với

A. SC     

B. SB   

C. SD     

D. CD

   b) Khoảng cách từ D đến mặt phẳng (SAC) bằng:

Câu 8: Cho hình lập phương ABCD.A’B’C’D’:

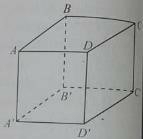
a) Mặt phẳng (ACC’A’) không vuông góc với.

A. (ABCD)     

B. (CDD’C’)

C. (BDC’)     

D. (A’BD)

   b) Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:

A.  trung điểm của BD

B.   trung điểm của A’B

C.   trung điểm của A’D   

D. tâm của tam giác BDA’

   Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.

Câu 9: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.

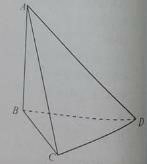
   a) Đường thẳng AB vuông góc với

A.  (BCD)

B.   (ACD)

C.   (ABC)

D.  (CID) với I là trung điểm của AB.

   b) Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?

A.  Không vuông góc với mặt nào?

B.   (ACD)      C. (ABC)      D. (BCD)

   c) Đường vuông góc chung của AB và CD là:

   A. AC      B. BC      C. AD      D. BD

Lời giải:

Đáp án: a - A, b - D, c - B

a.   AB ⊥ CD và AB ⊥ CD ⇒ AB ⊥ (BCD)

b.  vì AB ⊥ (BCD) ⇒ (ABD) ⊥ (BCD)

c.   BC ⊥ AB và BC ⊥ CD ⇒ BC là đường vuông góc chung của AB và CD

Câu 10: Cho hình hộp chữ nhật ABCD.A′B′C′D′ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng?

A.  Tồn tại điểm O cách đều tám đỉnh của hình hộp.

B.   Hình hộp có 6 mặt là 6 hình chữ nhật.

C.  Hai mặt ACC′A′ACC'A' và BDD′B′BDD'B' vuông góc nhau.

D.  Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.

Lời giải:

Đáp án: C

Giải thích:

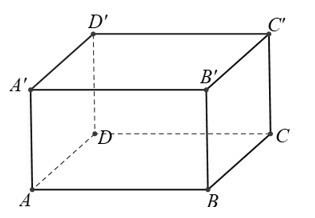
Câu 11: Cho hình chóp S.ABCS.ABC có SA⊥(ABC)SA⊥ABC và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC)SBC. Khẳng định nào sau đây đúng?

A.    H∈SBH∈SB

B.     H trùng với trọng tâm tam giác SBC.

C.    H∈SCH∈SC

D.    H∈SIH∈SI (I là trung điểm của BC).

Lời giải:

Đáp án: D

Giải thích:

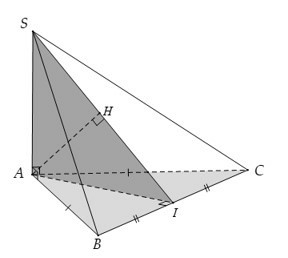
Gọi I là trung điểm của BC

⇒AI⊥BC⇒AI⊥BC mà BC⊥SABC⊥SA 

⇒BC⊥(SAI)⇒BC⊥SAI

Khi đó H là hình chiếu vuông góc của A lên (SBC)SBC.

Suy ra H∈SIH∈SI.

Câu 12: Trong các mệnh đề sau, mệnh đề nào đúng?

A.  Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.

B.  Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

C.  Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.

D.  Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.

Lời giải:

Đáp án: C

Giải thích: Đường thẳng thỏa mãn cần tìm là đường thẳng đi qua điểm A cho trước và vuông góc với mặt phẳng (P) cho trước. Đây là đường thẳng cố định. Câu 13: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng?

A.  Có ba cặp mặt phẳng vuông góc với nhau

B.   Có hai cặp mặt phẳng vuông góc với nhau

C.  Có năm cặp mặt phẳng vuông góc với nhau

D.  Có bốn cặp mặt phẳng vuông góc với nhau

Lời giải:

Đáp án: C

Giải thích:

Xét hình chóp S.ABCD có đáy là hình vuông và SA ⊥ (ABCD)

+ Do SA ⊂ (SAB) và SA ⊥ (ABCD) nên (SAB) ⊥ (ABCD)

+ Do SA ⊂ (SAD) và SA ⊥ (ABCD) nên (SAD) ⊥ (ABCD)

+ Do AD ⊥ SA, AD ⊥ AB nên AD ⊥ ( SAB)

AD ⊂ (SAD) và AD ⊥ (SAB) nên (SAD) ⊥ (SAB).

+ Chứng minh tương tự; ta có: (SAD) ⊥ (SCD) và (SAB) ⊥ (SBC).

⇒ có tất cả năm cặp mặt phẳng vuông góc với nhau.

Câu 14: Trong các mệnh đề sau, mệnh đề nào đúng?

A.  Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

B.   Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

C.  Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

D.  Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

Lời giải:

Đáp án: B

Giải thích:

Chọn đáp án B

A  sai vì đáy có thể là hình bình hành.

B   đúng

C   sai vì đáy có thể là hình bình hành

D  sai vì đáy có thể là hình bình hành.

Câu 15: Mệnh đề nào sau đây là đúng?

A.              Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.

B.              Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.

C.              Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

D.              Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.

Lời giải:

Đáp án: D Giải thích:

Mệnh đề A sai vì có thể xảy ra trường hợp hai mặt phẳng vuông góc với nhau nhưng đường thẳng thuộc mặt phẳng này song song với mặt phẳng kia.

Mệnh đề B sai vì xảy ra trường hợp hai mặt phẳng song song.

Mệnh đề C sai vì xảy ra trường hợp hai mặt phẳng vuông góc.

Chọn đáp án D

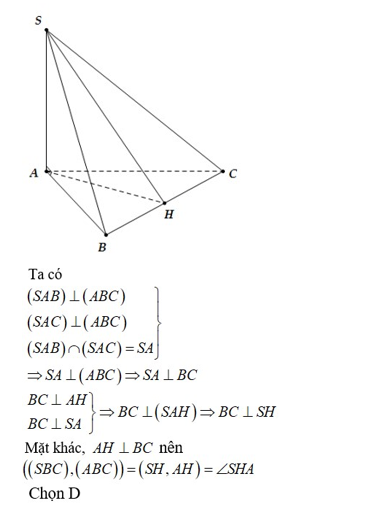
Câu 16: Cho hình chóp S.ABC có hai mặt bên (SAB) và(SAC) vuông góc với mặt phẳng (ABC) , tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC) . Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây sai ?

A.  SA ⊥ (ABC)

B.   O ∈ SH

C.  (SAH) ⊥ (SBC) D. ((SBC), (ABC)) = ∠SBA

Lời giải:

Đáp án: D

Giải thích:

Câu 17: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD

= 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF)và (SBC)

là

A.  90°                    

B.   60°                    

C.  30°                    

D.  45°

Lời giải:

Đáp án: A

Giải thích:

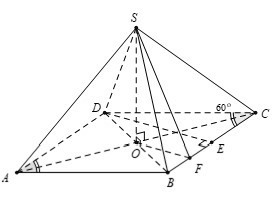
Tam giác BCD có BC = BD và ∠BCD = 60° nên tam giác BCD đều

Lại có E là trung điểm BC ⇒ DE ⊥ BC

Mặt khác, tam giác BDE có OF là đường trung bình ⇒ OF // DE ⇒ BC ⊥ OF   (1).

+ Do SO ⊥ (ABCD) ⇒ BC ⊥ SO  (2).

+ Từ (1) và (2), suy ra BC ⊥ (SOF) ⇒ (SBC) ⊥ (sOF)

Vậy, góc giữa ( SOF) và( SBC) bằng 90°

Câu 18: Cho hình chóp S. ABC có SA ⊥ (ABC) và AB ⊥ BC , gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây? A. Góc SBA.          

B.   Góc SCA.          

C.  Góc SCB.          

D.  Góc SIA.

Lời giải:

Đáp án: A

Giải thích:

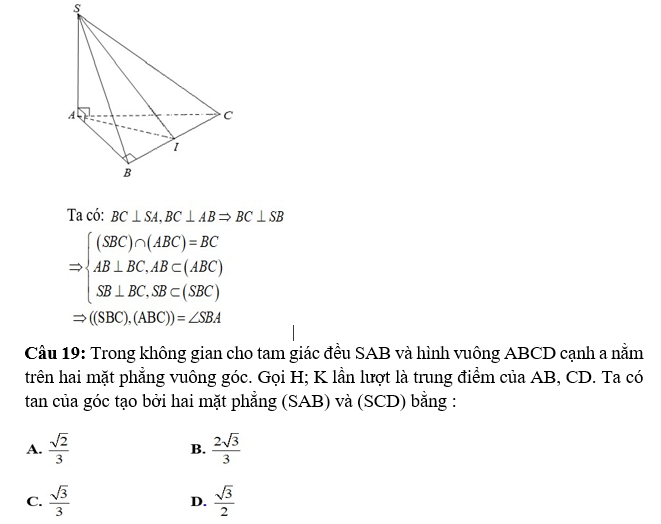
Lời giải:

Đáp án: B

Giải thích:

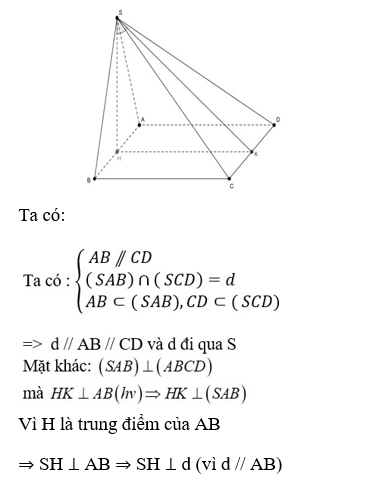
⇒ d ⊥ SK (theo định lý ba đường vuông góc)

Do đó: ∠KSH = α là góc giữa (SAB) và (SCD)

Mà SH là đường cao trong tam giác SAB đều cạnh a ⇒ SH = a√3/2 Xét tam giác SHK vuông tại H có:

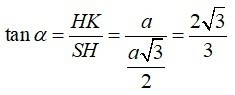
Câu 20: Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC’ = c. Nếu AC' = BD' = B'D = √(a² + b² + c²) thì hình hộp là

A.  Hình lập phương

B.   Hình hộp chữ nhật

C.  Hình hộp thoi D. Hình hộp đứng

Lời giải:

Đáp án: B

Giải thích:

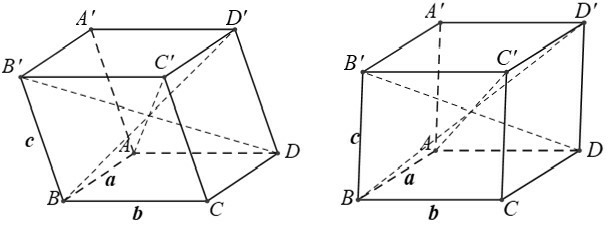
Nếu AC’= BD’  hình bình hành ABC’D’ là hình chữ nhật Nếu BD’= B’D  hình bình hành BDD’B’ là hình chữ nhật

Nếu AC’= B’D  hình bình hành ADC’B’ là hình chữ nhật  nếu AC’ = BD’ = B’D thì hình hộp là hình hộp chữ nhật.

Chọn B

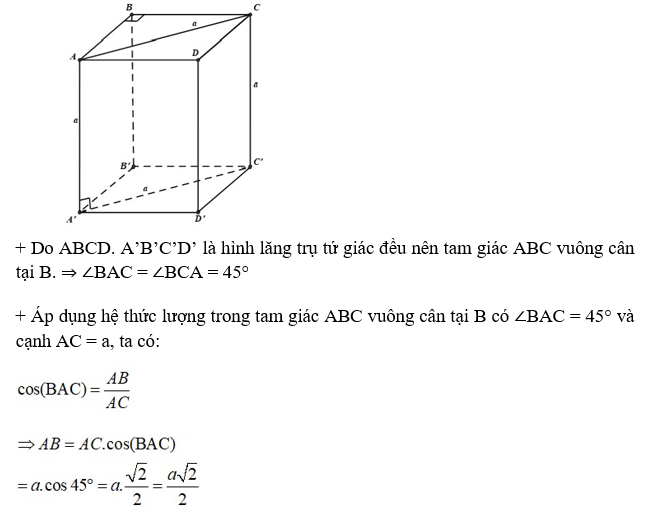
Câu 21: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC’A’ là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:

Lời giải:

Đáp án: A

Giải thích:

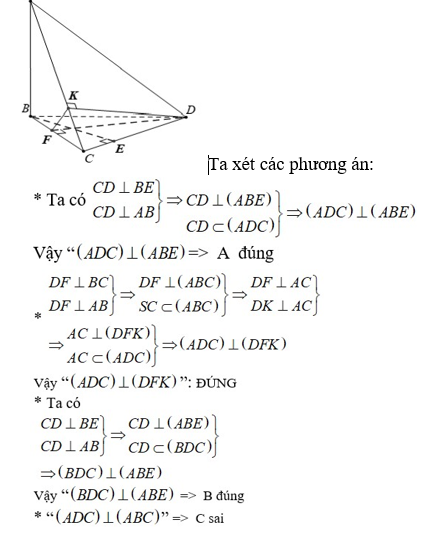
Câu 22: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?

A.  (ADC) ⊥ (ABE)           

B.   (ADC) ⊥ (DFK)

C.  (ADC) ⊥ (ABC)            

D.  (BDC) ⊥ (ABE)

Lời giải:

Đáp án: C

Giải thích:

Câu 23: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A.  H ∈ SB

B.   H trùng với trọng tâm tam giác SBC.

C.  H ∈ SC

D.  H ∈ SI (I là trung điểm của BC).

Lời giải:

Đáp án: D

Giải thích: 

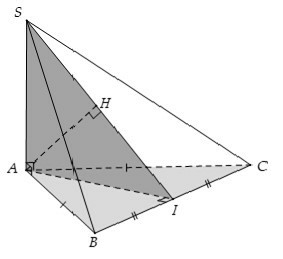
Gọi I là trung điểm của BC

⇒ AI ⊥ BC mà BC ⊥ SA ⇒ BC ⊥ (SAI)

⇒ SI ⊥ BC   (1)

Khi đó H là hình chiếu vuông góc của A lên (SBC) .

Suy ra AH ⊥ BC

Lại có: SA ⊥ BC

⇒ BC ⊥ (SAH) ⇒ BC ⊥ SH    (2)

Từ (1) và (2) suy ra 3 điểm S; H; I thẳng hàng.

Câu 24: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC’) có số đo bằng 60°. Cạnh bên của hình lăng trụ bằng:

A.  3a            

B.   a√3            

C.  2a            

D.  a√2

Lời giải:

Đáp án: A

Giải thích:

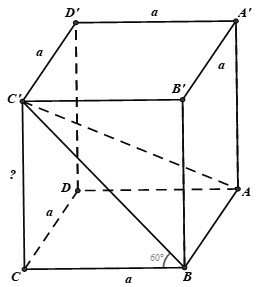
Chọn B.

Ta có: (ABCD) ∩ (ABC') = AB

Ta có: AB ⊥ BC và AB ⊥ BB' (vì lăng trụ đã cho là lăng trụ tứ giác đều)

⇒ AB ⊥ (BB'C'C) mà C'B ⊂ (BB'C'C) ⇒ AB ⊥ C'B

Mặt khác: CB ⊥ AB

⇒ ((ABCD), (ABC')) = (CB, C'B) = ∠ CBC' = 60°

Áp dụng hệ thức lượng trong tam giác BCC’ vuông tại C ta có: tan(CBC') = CC'/CB ⇒ CC' = CB.tan(CBC') = a.tan60° = a√3