Để hỗ trợ cho việc học và ôn tập kì thi học kì 1 của các bạn học sinh, Toptailieu.vn đăng tải bộ Đề cương ôn tập học kì 1 môn Toán lớp 6 Trường THCS Hoàng Mai- 2022- 2023 giúp các em nắm được nội dung kiến thức trọng tâm và đạt kết quả tốt trong kì thi sắp tới.

A.    LÍ THUYẾT

I- Giới hạn chương trình:

1) Số học và Đại số: Ôn các công thức, quy tắc trong chương I và chương II  SGK.

2) Hình học: Ôn từ bài “ Tam giác đều. Hình thoi. Hình vuông” đến bài “ Hình có tâm đối xứng”.

II- Ôn tập lý thuyết:

*) Số học và Đại số:

1) Nêu kí hiệu và cách viết một tập hợp? Phần tử của một tập hợp? Các cách cho một tập hợp? Thế nào tập hợp N và tập hợp N*?

2) Viết dạng tổng quát của các tính chất của phép cộng và phép nhân số tự nhiên.

3) Lũy thừa bậc n của a là gì? Viết các công thức nhân, chia hai lũy thừa cùng cơ số.

4) Phát biểu và viết dạng tổng quát tính chất chia hết của một tổng, tính chất chia hết của một tích?

5) Phát biểu các dấu hiệu chia hết cho 2; 3; 5; 9.

6) Thế nào là số nguyên tố, hợp số. Để chứng minh một số là hợp số ta làm như thế nào?

7) Khi nào a là bội của b và b là ước của a? Nêu cách tìm ước và bội. Nêu cách tìm ƯCLN và BCNN của hai hay nhiều số bằng cách phân tích ra thừa số nguyên tố. Lấy ví dụ minh họa cho từng trường hợp?

8) Nêu cách nhận biết số nguyên âm và các ứng dụng của số nguyên âm trong đời sống

9) Tập hợp các số nguyên âm bao gồm những số gì. Thế nào là hai số nguyên đối nhau. Nêu cách so sánh hai số nguyên?

10) Nêu các bước cộng hai số nguyên âm và cộng hai số nguyên khác dấu. Viết dạng tổng quát tính chất phép cộng các số nguyên.

11) Muốn trừ số nguyên a cho số nguyên b ta làm như thế nào, Nêu qui tắc bỏ dấu ngoặc?

12) Nêu các bước nhân (chia) hai số nguyên khác dấu và các bước nhân (chia) hai số nguyên âm. Lấy ví dụ minh họa. Nêu tính chất của phép nhân các số nguyên?

13) Khi nào số nguyên a chia hết cho số nguyên b, lấy ví dụ minh họa?

*) Hình học:

1) Nhận biết tam giác đều, hình vuông, lục giác đều, hình chữ nhật, hình thoi, hình bình hành, hình thang cân?

2) Nêu cách vẽ tam giác đều, hình vuông, hình chữ nhật, hình thoi, hình bình hành?

3) Nêu công thức tính chu vi, diện tích hình huông, hình chữ nhật, hình thoi, hình bình hành, hình thang cân?

4) Vẽ trục đối xứng của: Đoạn thẳng AB; đường tròn tâm O; Hình thang cân; hình lục giác đều; hình thoi; hình vuông; hình chữ nhật.

5) Hãy xác định tâm đối xứng của: Đoạn thẳng AB; đường tròn tâm O; hình thoi; hình bình hành; hình vuông?

B. BÀI TẬP

Các dạng bài tập

- Số học và Đại Số chương I , chương II

- Hình học từ bài “ Tam giác đều. Hình thoi. Hình vuông” đến bài “ Hình có tâm đối xứng”

Dạng 1: Tập hợp

Các kiến thức tập hợp trên tập hợp số tự nhiên và số nguyên.

Dạng 2: Các phép tính với số tự nhiên, số nguyên:

- Tính giá trị biểu thức với các phép tính : cộng, trừ, nhân, chia số tự nhiên, số nguyên.

- Các phép tính về lũy thừa

- Thứ tự thực hiện phép tính ( theo các quy tắc )

- Tìm x

Dạng 3: Tính chất chia hết của một tổng, dấu hiệu chia hết cho 2, 3, 5, 9, ƯCLN, BCNN.

- Nhận biết các số chia hết cho 2, 3, 5, 9.

- Tìm ƯCLN, BCNN; vận dụng trong bài toán  rút gọn phân số.

Dạng 4: Các bài toán có lời văn và liên quan ứng dụng thực tế:

-Sử dụng các kiến thức toán học giải quyết một số bài toán có tính ứng dụng thực tế

( Ví dụ: Bài 4, 5 SGK trang 17; Bài 40, 41 SBT- trang 17,…)

-Các bài toán thực tế áp dụng kiến thức ƯCLN, BCNN.

 (Ví dụ: bài 7,8 SGK trang 51, bài 6,7 SGK trang 58)

- Các bài toán vận dụng kiến thức về số nguyên.

( Ví dụ: bài 7,8 SGK trang 74,75,..)

Dạng 5: Hình học

1. Nhận biết các hình: tam giác đều, hình vuông, lục giác đều, hình chữ nhật, hình thoi, hình bình hành, hình thang cân. Nhận biết hình có tâm đối xứng, trục đối xứng.

2. Vẽ hình bằng thước và compa: vẽ các hình tam giác đều, hình vuông, hình chữ nhật, hình thoi, hình bình hành theo điều kiện cho trước.

3. Tính diện tích và chu vi các hình theo điều kiện đề bài cho.

Dạng 6. Bài tập nâng cao

- Chứng minh tính chia hết với số tự nhiên, số nguyên của biểu thức chứa chữ.

- Tính tổng của dãy số có quy luật.

- Bài tập về ước chung, bội chung, ước chung lớn nhất, bội chung nhỏ nhất, số nguyên tố, hợp số.

- So sánh 2 lũy thừa.

- Tìm chữ số tận cùng của một lũy thừa, một tích.

-Bài tập áp dụng quan quan hệ chia hết.

- Các bài toán suy luận logic.

MỘT SỐ BÀI TẬP THAM KHẢO

ÔN TẬP  HỌC KÌ I- NĂM HỌC 2022-2023

I. TRẮC NGHIỆM: Khoanh tròn chỉ một chữ cái đứng trước kết quả đúng:.

Câu 1:          Kết quả phép tính: \(237 \cdot ( - 28) + 28 \cdot 137\) là:

A. \( - 2800\).                                                       

B. 2800.

C. \( - 10472\).                                                     

D. Một đáp án khác.

Câu 2:          Cho \(\overline {630*} \) chia hết cho 5 và 9 thì * là:

A. 9                                

B. 0.                             

C. 5.                             

D. 3.

Câu 3:          Các ước nguyên tố a của 18 là

A. \(a \in \{ 1;2;3;6;9;18\} \).                              

B. \(a \in \{ 1;3;9\} \).

C. \(a \in \{ 1;2;3\} \).                                          

D. \(a \in \{ 2;3\} \).

Câu 4:          Trong tập các số nguyên sau, tập hợp nào được sắp xếp theo thứ tự giảm dần?

A. \(\{ 2;5;1; - 2;0; - 17\} \).                                

B. \(\{  - 2; - 17;0;1;2;5\} \).

C. \(\{  - 17; - 2;0;1;2;5\} \).                                

D. \(\{ 0;1;2;5; - 17\} \).

Câu 5:          Tổng của hai số nguyên tố bằng 9. Tích của hai số đó là

A. 8.                               

B. 14.                           

C. 18.                           

D. 20.

Câu 6:          Số 0:

A. Là ước của bất kì số tự nhiên nào.

B. Là hợp số.

C. Là bội của mọi số tự nhiên khác.

D. Là số nguyên tố.

Câu 7:          Tìm các số nguyên \(x\) sao cho \( - 3 < x \le 2\)

A. \(x \in \{  - 2; - 1;1;2\} \).

C. \(x \in \{  - 3; - 2; - 1;0;1;2\} \).

B. \(x \in \{  - 3; - 2; - 1;0;1\} \).

D. \(x \in \{  - 2; - 1;0;1;2\} \).

Câu 8:          Khi bỏ dấu ngoặc trong các biểu thức số: \(2003 - (5 - 9 + 2002)\), ta được:

A. \(2003 + 5 - 9 - 2002\).

B. \(2003 + 5 + 9 + 2002\).

C. \(2003 - 5 - 9 - 2002\).

D. \(2003 - 5 + 9 + 2002\).

Câu 9:          Khẳng định nào sau đây là SAI?

A. Tổng của hai số nguyên âm là một số nguyên âm.

B. Mọi số nguyên âm đều bé hơn số 0.

C. Hai số nguyên đối nhau có tổng bằng 0.

D. Hai số nguyên đối nhau có giá trị tuyệt đối bằng nhau.

Câu 10:      Tìm số nguyên \(x\) biết \(x + 3\) là ước nguyên âm nhỏ nhất của 15?

A. \(x =  - 18\).               

B. \(x =  - 2\).               

C. \(x =  - 3\).               

D. \(x =  - 4\).

Câu 11:      Cho tập hợp \(A = \{  - 3;2;0; - 1;5;7\} \). Viết tập hợp \(B\) gồm các phần từ là số đối của các phần tử trong tập hợp \(A\).

A. \(B = \{ 3; - 2;0;1; - 5;7\} \).                           

B. \(B = \{ 3; - 2;0; - 5; - 7\} \).

C. \(B = \{ 3; - 2;0;1; - 5; - 7\} \).                        

D. \(B = \{  - 3;2;0;1; - 5; - 7\} \).

Câu 12:      Cho hình thang cân \(PQRS\) có độ dài đáy \(PQ = 20{\rm{cm}}\), đáy \(RS\) ngắn hơn đáy \(PQ\) là \(12{\rm{cm}}\), độ dài cạnh bên \(PS\) bằng một nửa độ dài đáy \(PQ\). Chu vi của hình thang \(PQRS\) là

A. \(46{\rm{m}}\).           B. \(44{\rm{m}}\).        C. \(40{\rm{m}}\).        D. \(48{\rm{m}}\).

Câu 13:      Cho các hình bình hành \(ABCD,FBCE,AFED\) (hình vẽ bên). Tính diện tích hình bình hành \(FBCE\) biết diện tích hình bình hành \(ABCD\) là \(48{\rm{c}}{{\rm{m}}^2}\) và độ dài cạnh \(DC\) gấp 3 lần độ dài cạnh \(EC\).

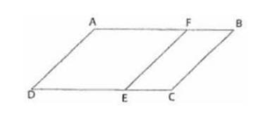
A. \(12{m^2}\)                B. \(14{m^2}\).             C. \(10{m^2}\).             D. \(16{{\rm{m}}^2}\).

Câu 14:      Biểu đồ bên cho biết số cây xanh được trồng chăm sóc của hai khối 8 và 9 của Trường THCS Hoàng Mai. Từ biểu đồ hãy cho biết khối 8 trồng chăm sóc nhiều hơn khối 9 bao nhiêu cây?

A. 20.                              B. 5.                              C. 10.                            D. 15.

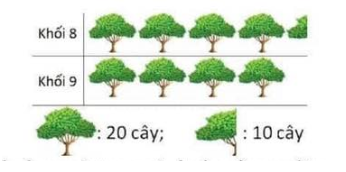
Câu 4: Trong các hình sau (bao gồm cả màu sắc), hình nào không có trục đối xứng?

A.   Hình 1                        B. Hình 2                     C. Hình 3                      D. Hình 4

II. TỰ LUẬN

DẠNG 1: THỰC HIỆN PHÉP TÍNH

Câu 1:          Thực hiện phép tính:

a) \(29 + 132 + 237 + 868 + 763\)

b) \(35 - \{ 12 - [ - 14 + ( - 2)]\} \)

c) \({4.5^5} - 32:{2^4}\)

d) \( - 452 - ( - 67 + 75 - 452)\)

e) \(1997 - \left[ {10 \cdot \left( {{4^3} - 56} \right):{2^3} + {2^3}} \right] \cdot 2005^\circ \)

f) \(5002^\circ  \cdot 18 + 99 \cdot 18 - \left( {{3^3} \cdot {3^2} + {2^4} \cdot 2} \right)\).

Câu 2:          Tính bằng cách hợp lí:

a) 24. \((16 - 5) - 16 \cdot (24 - 5)\)

b) \(29.(19 - 13) - 19.(29 - 13)\)

c) \(31 \cdot ( - 18) + 31 \cdot ( - 81) - 31\)

d) \(( - 12) \cdot 47 + ( - 12) \cdot 52 + ( - 12)\)

e) \(13 \cdot (23 + 22) - 3 \cdot (17 + 28)\)

f) \( - 48 + 48 \cdot ( - 78) + 48 \cdot ( - 21)\)

DẠNG 2: TÌM \(x\)

Câu 1:          Tìm số tự nhiên \(x\), biết:

a) \(121 - (118 - x) = 217\)

b) 8) \(7x - x = {5^{21}}:{5^{19}} + {3.2^2} - 7\)

c) \([(6x - 39):7].4 = 12\)

d) \(11x - 7x + x = 325\)

e) \(\left( {3x - {2^4}} \right) \cdot {7^3} = 2 \cdot {7^4}\)

f) \((2x - 4) \cdot (3 - x) = 0\).

Câu 2:          Tìm số nguyên \(x\) thỏa mãn:

a) \([230 - (15 - 5x)].3 = 390\)

b) \(345 - {5^{x - 3}} = {14^2} + 24\)

c) \(x - [42 + ( - 28)] =  - 8\)

d) \(720:[41 - (2x - 5)] = {2^2}.5\)

e) \(15 - x = 7 - ( - 2)\)

f) \({(2x - 1)^3} = 8\).

Câu 3:          Tìm số nguyên \(x\) sao cho:

a) \([3.(x + 1) + 25]:5;9 \le x \le 15\)

b) \(70 \vdots x,84 \vdots x,120 \vdots x\)

c) \((2x + 3) \vdots (3x + 2)\)

d) \(x \vdots 4,x \vdots 7,x \vdots 8\) và \(x\) nhỏ nhất khác 0.

e) \(24 \vdots x,36 \vdots x,160 \vdots x\) và \(x\) lớn nhất.

f) \(x \vdots 25\) và \(0 < x < 100\)

DẠNG 3: CÁC BÀI TOÁN CÓ NỘI DUNG THỰC TẾ

Câu 1:          Mỗi công nhân đội I làm 24 sản phẩm, mỗi công nhân đội II làm 20 sản phẩm. Số sản phẩm hai đội làm bằng nhau. Tính số sản phẩm mỗi đội biết số sản phẩm đó từ khoảng 100 đến 210.

Câu 2:          Hai bạn Tùng và Hải đều đến thư viện đề đọc sách. Tùng cứ 8 ngày đến thư viện một lần, Hải cứ 10 ngày đến thư viện một ngày. Lần đầu hai bạn vào thư viện cùng một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn lại cùng đến thư viện?.

Câu 3:          Một khối học sinh khi tham gia diễu hành nếu xếp hàng \(12;15;18\) đều thiếu 7. Hỏi khối có bao nhiêu học sinh? Biết rằng số học sinh trong khoảng 350 đến 400 em.

Câu 4:          Ba khối lớp 6, 7, 8 có 300, 276, 252 học sinh cùng xếp hàng sao cho số hàng dọc của các khối là như nhau. Hỏi các khối có thể xếp được nhiều nhất bao nhiêu hàng dọc mà không ai lẻ hàng?

Câu 5:          Số học sinh khối 6 của trường trong khoảng từ 200 đến 500. Khi xếp hàng 18, 12, 15 thì đều thừa 4 học sinh. Tính số học sinh đó.

Câu 6:          Nhà trưởng tổ chức cho học sinh đi tham quan bảo tàng. Tính số học sinh tham quan biết rằng nếu xếp mỗi xe 36, 40 hay 45 học sinh đều vừa đủ và số học sinh trong khoảng từ 1000 đến 1100 em.

Câu 7:          Một chiếc tàu ngầm đang ở độ cao -25m so với mực nước biển, tàu tiếp tục lặn xuống thêm 10m nữa. Độ cao mới của tàu so với mực nước biển là bao nhiêu mét ?

Câu 8:          Một nhà hàng hải sản nợ ngân hàng 30 triệu đồng, sau đó nhà hàng đã trả nợ ngân hàng 10 triệu đồng. Số dư tài khoản của nhà hàng ở ngân hàng là bao nhiêu?

Câu 9:          Công ty Phú Quý có lợi nhuận mỗi tháng trong Quý III là 20 triệu đồng. Trong Quý IV, lợi nhuận mỗi tháng của công ty là -10 triệu đồng. Trong 6 tháng cuối năm, lợi nhuận của công ty Phú Quý là bao nhiêu tiền ?

DẠNG 4: HÌNH HỌC TRỰC QUAN

Câu 1:          Vẽ các hình sau (Không cần nêu cách vẽ):

a) Hình tam giác đều \(ABC\) có cạnh là \(3{\rm{cm}}\).

b) Hình vuông \(ABCD\) có cạnh bằng \(4{\rm{cm}}\).

c) Hình chữ nhật \(MNPQ\) có chiều dài \(MN\) \( = 8{\rm{cm}}\), chiều rộng \(NP\) \( = 6{\rm{cm}}\)

d) Hinh thoi \(EFGH\) có \(EF = 3{\rm{cm}},EG = 5{\rm{cm}}\).

e) Hình bình hành \(GHIK\) có \(GH = 3{\rm{cm}},HI = 5{\rm{cm}}\).

Câu 2:          Tính chu vi và diện tích các hình sau:

a) Hình chữ nhật có chiều dài \(20{\rm{cm}}\) và chiều rộng \(12{\rm{cm}}\).

b) Hình vuông có cạnh \(5{\rm{cm}}\).

c) Hình thang cân có độ dài hai đáy là \(4{\rm{cm}}\) và \(10{\rm{cm}}\), chiều cao \(4{\rm{cm}}\), cạnh bên \(5{\rm{cm}}\).

d) Hình thoi có cạnh \(5dm\), độ dài hai đường chéo là \(60{\rm{cm}}\) và \(80{\rm{cm}}\).

e) Hình bình hành có độ dài hai cạnh là \(12{\rm{cm}}\) và \(16{\rm{cm}}\), chiều cao \(10{\rm{cm}}\).

Câu 3: 

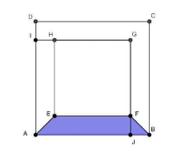
     Cho hình vuông \(ABCD\) có \(AB = 30{\rm{cm}}\), hình vuông \(EFGH\) có \(EF = 24{\rm{cm}}\), biết \(AIGJ\) là một hình vuông và \(ABFE\) là một hình thang cân (hình vẽ bên). Tính diện tích hình vuông \(AIGJ\) và diện tích hình thang cân \(ABFE\).

Câu 4:

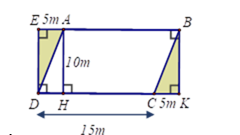
               Một khu đất có dạng hình bình hành ABCD có cạnh DC = 15m, đường cao AH = 10cm.

1) Tính diện tích khu đất.

2) Người chủ muốn mở rộng khu đất về hai phía như hình vẽ. Biết sau khi mở rộng, khu đất có dạng hình chữ nhật EBKD. Tính diện tích phần mở rộng thêm.

Câu 5: Một thửa ruộng hình thang có các kích thước như hình dưới.

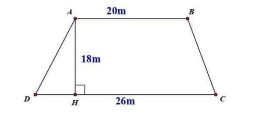
            Tính diện tích mảnh ruộng.

Câu 6: Một phòng họp hình chữ nhật có các kích thước như hình dưới. Biết rằng cứ mỗi \(6{{\rm{m}}^2}\) là người ta xếp vào đó 4 cái ghế sao cho đều nhau và kín phòng học.

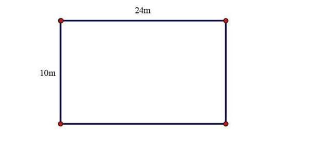
a) Tính diện tích phòng học.

b) Hỏi phòng đó có bao nhiêu ghế?

Câu 7: Một mảnh vườn hình thoi có độ dài hai hai đường chéo là \(9{\rm{m}}\) và \(6{\rm{m}}\). Ở giữa vườn người ta xây một bể cá hình vuông có độ dài mỗi cạnh là \(2{\rm{m}}\), và phần còn lại để trồng hoa. Tính diện tích phần vườn trồng hoa.

Câu 8: Một thửa ruộng hình thang có diện tích là \(1155{{\rm{m}}^2}\) và có đáy bé kém đáy lớn. Người ta kéo dài đáy bé thêm \(20{\rm{m}}\) và kéo dài đáy lớn thêm \(5m\) về cùng một phía để được hình thang mới. Diện tích hình thang mới này bằng diện tích của một hình chữ nhật có chiều rộng là \(30{\rm{m}}\) và chiều dài \(51{\rm{m}}\). Hãy tính đáy bé, đáy lớn của thửa ruộng ban đầu.

DẠNG 6: BÀI TẬP NÂNG CAO

Câu 1:          Chứng minh rằng: \(2 + {2^2} + {2^3} + {2^4} +  \ldots  + {2^{59}} + {2^{60}}\) chia hết cho 3.

Câu 2:          Cho \(A = 7 + {7^2} + {7^3} +  \ldots . + {7^{11}} + {7^{12}}\)

a) \(A\) là số chẵn hay số lẻ? Vì sao?

b) \(A\) là số nguyên tố hay hợp số, vì sao?

c) Tìm chữ số tận cùng của \(A\).

Câu 3:          Tìm số nguyên tố \(p\), \(q\) sao cho:

a) \(p + 4;p + 10\) là số nguyên tố

b) \(q + 2;q + 8\) là số nguyên tố.

Câu 4:          Tìm số tự nhiên \(a\), \(b\) biết

1) \(a + b = 40\) và ƯCLN(a;b)=5              2) \(a.b = 768\) và ƯCLN(a;b)=8

Câu 5:          Số nguyên \(x\), \(y\) biết:

a) \(x + xy + y = 9\)

b) \(3x(y + 2) + y + 2 = 13\)

c) \(xy - x + 3y - 2 = 6\).

 Câu 6: Chứng minh rằng:

a) 5n + 1 và 6n + 1 (\(n \in N\)) nguyên tố cùng nhau.

b) ƯCLN(a;b)=ƯCLN(3a+2b;4a+3b).