Trả lời câu hỏi giữa bài:

Luyện tập 1 trang 6 Toán lớp 6 Tập 1: Gọi B là tập hợp các bạn tổ trưởng trong lớp em. Em hãy nêu tên một bạn thuộc tập B và một bạn không thuộc tập B.

Phương pháp giải:

Tất cả các bạn tổ trưởng trong lớp em đều thuộc B.

Một bạn thuộc B: Em tìm một bạn tổ trưởng.

Một bạn không thuộc B: bạn không là tổ trưởng.

Lời giải:

Tất cả các bạn tổ trưởng trong lớp em đều thuộc B.

Ví dụ: An, Minh, Tâm, Huy, Khang, Ngọc

Một bạn thuộc B: Em tìm một bạn tổ trưởng.

Ví dụ: Tâm

Một bạn không thuộc B: bạn không là tổ trưởng.

Ví dụ: Linh Chi

Câu hỏi trang 7 SGK Toán lớp 6 Tập 1: Khi mô tả tập hợp L các chữ cái trong từ NHATRANG bằng cách liệt kê các phần tử, bạn Nam viết:

L = {N, H, A, T, R A, N, G}.

Theo em, bạn Nam viết đúng hay sai?

Phương pháp giải:

Cách mô tả tập hợp: Liệt kê các phần tử của tập hợp, tức là viết các phần tử trong dấu ngoặc {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.

Lời giải:

Bạn Nam viết sai vì mỗi phần tử chỉ được viết một lần mà phần tử A và N bạn Nam viết 2 lần.

Cách viết đúng: L = {N;H;A;T;R;G}

Với giải Luyện tập 2 trang 7 SGK Toán lớp 6 Tập 1 Kết nối tri thức và cuộc sống chi tiết trong Bài 1: Tập hợp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:

Luyện tập 2 trang 7 SGK Toán lớp 6 Tập 1: Viết các tập hợp sau bằng cách liệt kê các phần tử của chúng:

A = {x∈∈NN| x < 5}

B = {x∈N∗x∈N∗| x < 5}

Phương pháp giải:

+Cách viết các tập hợp sau bằng cách liệt kê các phần tử: Liệt kê các phần tử của tập hợp, tức là viết các phần tử trong dấu ngoặc {} theo thứ tự tùy ý, các phần tử ngăn cách nhau bởi dấu ; nhưng mỗi phần tử chỉ được viết một lần.

+ N là tập hợp các số tự nhiên và N* là tập hợp các số tự nhiên khác 0

Lời giải:

Ta có:

A = {0; 1; 2; 3; 4}

B = {1; 2; 3; 4}

Luyện tập 3 trang 7 SGK Toán lớp 6 Tập 1: Gọi M là tập hợp các số tự nhiên lớn hơn 6 và nhỏ hơn 10.
a) Thay thế dấu "?" bằng dấu ∈;∉∈;∉

15[?] M, 9[?]M,

b) Mô tả tập hợp M bằng hai cách.

Phương pháp giải:

Viết tập hợp M bằng hai cách liệt kê và chỉ ra tính chất đặc trưng.

Lời giải:

a) Các phần tử của tập hợp M là: 7; 8; 9. Do đó:

15∉M;9∈M15∉M;9∈M

b)

M={7;8;9}M={x∈N|6<x<10}M={7;8;9}M={x∈N|6<x<10}.

Bài tập trang 7 SGK Toán 6 Tập 1

Bài 1.1 trang 7 SGK Toán lớp 6 Tập 1: Cho hai tập hợp:

A = {a, b,c, x, y} và B = {b, d, y, t, u,v}.

Dùng kí hiệu “∈∈” hoặc “∉∉” để trả lời câu hỏi: Mỗi phần tử a, b, x, u thuộc tập hợp nào và không thuộc tập hợp nào?

Phương pháp giải:

- Lý thuyết về phần tử thuộc và không thuộc một tập hợp.

- Quan sát từng phần tử a, b, x, u, nếu phần tử nào xuất hiện trong tập hợp A thì ta viết “∈∈” tập đó, nếu phần tử đó không xuất hiện trong tập hợp A thì kí hiệu “∉∉”.

Lời giải:

Phần tử a thuộc tập hợp A và không thuộc tập hợp B nên ta kí hiệu:a∈A;a∉Ba∈A;a∉B

Tương tự với các phần tử khác:

b∈A;b∈Bb∈A;b∈B;

x∈A;x∉Bx∈A;x∉B

u∉A;u∈B

Bài 1.2 trang 7 SGK Toán lớp 6 Tập 1: Cho tập hợp hợp U = {x∈Nx∈N| x chia hết cho 3}.

Trong các số 3, 5, 6, 0, 7 số nào thuộc và số nào không thuộc tập hợp U

Phương pháp giải:

Một số thuộc tập U nếu số đó chia hết cho 3.

Các số có tổng các chữ số là một số chia hết cho 3 thì chia hết cho 3.

Lời giải:

Tập hợp U là tập hợp các số tự nhiên chia hết cho 3.

Số 3 là số tự nhiên chia hết cho 3 nên 3 thuộc U

Số 5 là số tự nhiên không chia hết cho 3 nên 5 không thuộc U

Tương tự, số 6 và số 0 thuộc U. Số 7 không thuộc U.

Bài 1.3 trang 7 SGK Toán lớp 6 Tập 1: Bằng cách liệt kê các phần tử, hãy viết các tập hợp sau:

a) Tập hợp K các số tự nhiên nhỏ hơn 7;

b) Tập hợp D tên các tháng (dương lịch) có 30 ngày;

c) Tập hợp M các chữ cái tiếng Việt trong từ “ ĐIỆN BIÊN PHỦ”

Phương pháp giải:

a)

-  Liệt kê các số tự nhiên, số nào nhỏ hơn 7 thì số đó là phần tử của K.

- Viết các số đó trong dấu ngoặc {} và các số đó chỉ được viết một lần.

b)

- Tìm các tháng (dương lịch) có 30 ngày.

- Viết tên các tháng đó trong dấu ngoặc {} và các tháng đó chỉ được viết một lần.

c)

- Liệt kê các chữ cái xuất hiện trong từ.

- Viết từng chữ cái trong dấu ngoặc {} và các chữ cái đó chỉ được viết một lần.

Lời giải:

a) Các số tự nhiên nhỏ hơn 7 là: 0;1;2;3;4;5;6

=> K = {0;1;2;3;4;5;6}

b) Các tháng dương lịch có 30 ngày là: Tháng 4, tháng 6, tháng 9, tháng 11.

=>  D = {tháng 4; tháng 6; tháng 9; tháng 11}

c) M = {Đ;I;Ê;N;B;P;H;U}

Bài 1.4 trang 8 SGK Toán lớp 6 Tập 1: Bằng cách nêu dấu hiệu đặc trưng, hãy viết các tập hợp A các số tự nhiên nhỏ hơn 10.

Phương pháp giải:

- Chỉ ra tính chất đặc trưng của các phần tử.

- Ta viết n∈Nn∈N có nghĩa n là một số tự nhiên.

Lời giải:

Tính chất đặc trưng của phần tử là nhỏ hơn 10.

Cách 1:

A={n| n là số tự nhiên nhỏ hơn 10}.

Cách 2:

A={n|n∈N,n<10}A={n|n∈N,n<10}.

Cách 3:

A={n∈N|n<10}A={n∈N|n<10}.

Bài 1.5 trang 8 SGK Toán lớp 6 Tập 1: Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quay quanh Mặt Trời gọi là các hành tinh. Đó là Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương và Sao Hải Vương. Gọi S là tập các hành tinh của Hệ Mặt Trời. Hãy viết tập S bằng cách liệt kê các phần tử của S.

Phương pháp giải:

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ” 

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Lời giải:

S = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}

Lý thuyết Tập hợp Toán 6

I. Tập hợp, phần tử

Giới thiệu

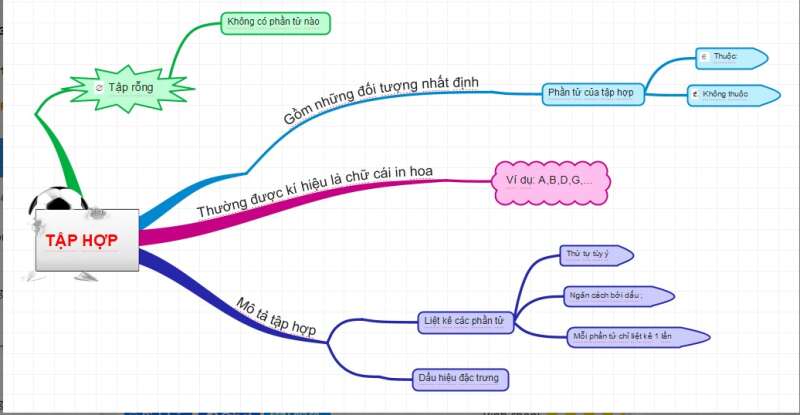
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.

Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.

Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.

+ Ví dụ:

a) Tập hợp các bạn nữ trong lớp 6A bao gồm tất cả các bạn nữ của lớp 6A. Đối tượng của tập hợp này là các bạn nữ của lớp 6A. Mỗi một bạn là một phần tử.

b) Tập hợp các số nhỏ hơn gồm tất cả các số nhỏ hơn 6, đó là 0,1,2,3,4,5. Mỗi một số trong 6 số này là một phần tử của tập hợp, chẳng hạn số 0 là một phần tử, số 1 cũng là một phần tử.

II. Các kí hiệu tập hợp

+) Ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D,...

+) Sử dụng các chữ cái thường a,b,c,... để kí hiệu cho phần tử.

+) Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu “;”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

+) Phần tử $x$ thuộc tập hợp $A$ được kí hiệu là $x\in A$, đọc là “x thuộc A”. Phần tử $y$ không thuộc tập hợp $A$ được kí hiệu là $y\notin A$, đọc là “y không thuộc A”.

Ví dụ: Tập hợp B gồm tất cả các số nhỏ hơn 5

Kí hiệu: $B=\left\{0;1;2;3;4\right\}=\left\{2;1;0;3;4\right\}$. Mỗi số 0;1;2;3;4 đều là một phần tử của tập hợp B. Số 6 không là phần tử của B( 8 không thuộc B)

Ta viết $0\in B;1\in B;2\in B;$$3\in B;4\in B$ và $8\notin B$

Ta không được viết $B=\left\{0;\underset{\_}{1;1};2;3;4\right\}$ cách viết này có hai số 1 là cách viết sai.

III. Các cách cho một tập hợp

1. Các cách cho một tập hợp

Cách 1:  Liệt kê các phần tử của tập hợp

Kí hiệu: $B=\left\{0;1;2;3;4\right\}=\left\{2;1;0;3;4\right\}$

Chú ý:

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ” (nếu có phần tử số) hoặc dấu “ ,”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó

Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).

a) Tập hợp B gồm tất cả các số nhỏ hơn 5

Liệt kê: $B=\left\{0;1;2;3;4\right\}=\left\{2;1;0;3;4\right\}$

Chỉ ra tính chất đặc trưng: $B=\{x|x<5\}$

b) Tập hợp các số nhỏ hơn 6

Liệt kê:  $A=\left\{0;1;2;3;4;5\right\}$

Chỉ ra tính chất đặc trưng: $B=\{x\in N|x<6\}$

Sơ đồ Venn:

 

2. Tập rỗng

Tập rỗng là tập hợp không có phần tử nào, kí hiệu $\mathrm{\varnothing }$.

Ví dụ:

Giả sử lớp 6A là một lớp không có bạn nào trên 55kg. Nên tập hợp các bạn trên 55kg của lớp 6A là tập rỗng.

IV. Tập hợp N và N*

Các số $0,1,2,3,4,...$ là các số tự nhiên

Tập hợp các số tự nhiên được kí hiệu là $\mathbb{N}$, tức là $\mathbb{N}=\left\{0;1;2;3;...\right\}$

Tập hợp các số tự nhiên khác 0 được kí hiệu là ${\mathbb{N}}^{\ast }$, tức là ${\mathbb{N}}^{\ast }=\left\{1;2;3;...\right\}$

Tập hợp $\mathbb{N}$ bỏ đi số 0 thì được ${\mathbb{N}}^{\ast }$.

Khi cho một số tự nhiên $x\in {\mathbb{N}}^{\ast }$ thì ta hiểu $x$ là số tự nhiên khác 0.

Ví dụ:

Viết tập hợp sau bằng cách liệt kê các phần tử: $A=\left\{a\in {\mathbb{N}}^{\ast }|a<4\right\}$

$a\in {\mathbb{N}}^{\ast }$ nên $a$ là các số từ 1;2;3;4;5;6;...

Tuy nhiên thêm điều kiện $a<4$ nên $a$ là các số 1;2;3.

Vậy $A=\left\{1;2;3\right\}$

 

Các dạng toán về tập hợp