Toptailieu.vn giới thiệu Giải bài tập Toán lớp 6 Bài 3: Thứ tự trong tập hợp các số tự nhiên sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6 Tập 1. Mời các bạn đón xem:
Toán 6 (Kết nối tri thức) Bài 3: Thứ tự trong tập hợp các số tự nhiên
Trả lời câu hỏi giữa bài:
Phương pháp giải:
Quan sát tia số và trả lời
Lời giải:
Điểm 5 nằm bên trái điếm 8, điểm 8 nằm bên phải điếm 5.
Điểm biểu diễn số tự nhiên nào nằm ngay bên phải điểm 8?
Phương pháp giải:
Quan sát tia số, điểm biểu diễn số nhỏ hơn thì nằm bên trái điểm biểu diễn số lớn hơn
Lời giải:
Điểm 7 biểu diễn số tự nhiên nằm ngay bên trái điểm 8.
Điểm 9 biểu diễn số tự nhiên nằm ngay bên phải điểm 8
Phương pháp giải:
Quan sát tia số, điểm biểu diễn số nhỏ hơn thì nằm bên trái điểm biểu diễn số lớn hơn
Lời giải:
n là một số tự nhiên nhỏ hơn 7 thì điểm n nằm bên trái điểm 7
b) Trên tia số (nằm ngang), trong hai điểm m và n, điểm nào nằm trước?
Phương pháp giải:
a) So sánh hai số m và n có số chữ số bằng nhau. Đi từ trái sang phải, so sánh các chữ số ở các hàng tương ứng.
b) Trên tia số, điểm nào nhỏ hơn thì điểm đó nằm trước điểm còn lại
Lời giải:
a) Vì hàng chục triệu, triệu, trăm nghìn, chục nghìn có các chữ số giống nhau, nhưng ở hàng nghìn ta thấy 6 > 5 nên 12 036 001 > 12 035 987. Vậy m>n
b) Vì m>n nên trên tia số điểm n nằm trước điểm m
Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều,
Số tiền thu được vào buổi tối ít hơn vào buổi chiều
Hãy so sánh số tiền thu được (đều là số tự nhiên) của cửa hàng đó vào buổi sáng và buổi tối.
Phương pháp giải:
Gọi số tiền cửa hàng đó thu được vào buổi sáng, buổi chiều và buổi tối lần lượt là a, b, c. Dựa vào đề bài so sánh a,b,c
Lời giải:
Gọi số tiền cửa hàng đó thu được vào buổi sáng, buổi chiều và buổi tối lần lượt là a, b, c (a, b, c là các số tự nhiên)
Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều nên a > b
Số tiền thu được vào buổi tối ít hơn vào buổi chiều nên c < b hay b > c
Theo tính chất bắc cầu ta được: a > c
Vậy số tiền thu được vào buổi sáng nhiều hơn vào buổi tối
Câu hỏi trang 14 SGK Toán lớp 6 Tập 1:Trong các số 3;5;8;9 số nào thuộc tập hợp A= {x∈N|x≥5}, số nào thuộc tập hợp B= {x∈N|x≤5}?...
Phương pháp giải:
Ta có thể mô tả lại tập hợp bằng cách liệt kê
Lời giải:
A={5;6;7;8;...}
B={0;1;2;3;4;5}
Ta có: 5,8,9∈A
3,5∈B
Bài tập trang 14 SGK Toán lớp 6 Tập 1
Bài 1.13 trang 14 SGK Toán lớp 6 Tập 1: Viết thêm các số liền trước và liền sau của hai số 3 532 và 3 529 để được sáu số tự nhiên rồi sắp xếp sáu số tự nhiên đó theo thứ tự từ bé đến lớn:
Phương pháp giải:
Viết thêm các số liền trước và liền sau của hai số 3 532 và 3 529 để được sáu số tự nhiên, rồi so sánh để viết sáu số tự nhiên đó theo thứ tự từ bé đến lớn.
Lời giải:
Các số liền trước và liền sau của số 3 532 là: 3 531 ; 3 533
Các số liền trước và liền sau của số 3529 là: 3 528 ; 3530
Sáu số trên được sắp xếp theo thứ tự từ bé đến lớn là:
3 528; 3 529; 3 530; 3 531; 3 532; 3 533
Bài 1.14 trang 14 SGK Toán lớp 6 Tập 1: Cho ba số tự nhiên a, b, c, trong đó a là số nhỏ nhất. Biết rằng trên tia số, điểm b nằm giữa hai điểm a và c. Hãy dùng kí hiệu "=" để mô tả thứ tự của ba số a, b, c. Cho ví dụ bằng số cụ thể.
Phương pháp giải:
Nếu a < b thì trên tia số, a nằm bên trái b .
Lời giải:
Số a nhỏ nhất nên điểm a nằm bên trái hai điểm b và c.
Mà điểm b nằm giữa hai điểm a và c nên điểm b nằm bên trái điểm c
Do đó b < c
Vì a bé nhất nên ta có a < b < c
* Ví dụ: a = 5; b = 7; c = 8
Số a bé nhất và điểm b nằm giữa hai điểm a và c trên tia số.
Bài 1.15 trang 14 SGK Toán lớp 6 Tập 1: Liệt kê các phần tử của mỗi tập hợp sau:
a) M={x∈N|10≤x<15}
b) K={x∈N*|x≤3}
c) L={x∈N|x≤3}
Phương pháp giải:
Liệt kê các phần tử của các tập hợp theo yêu cầu đề bài, mỗi phần tử chỉ viết 1 lần và cách nhau bởi dấu chấm phẩy.
Lời giải:
a) M = {10; 11; 12; 13; 14}
b) K = {1; 2; 3}
c) L = {0; 1; 2; 3}
Bài 1.16 trang 14 SGK Toán lớp 6 Tập 1: Ba bạn An, Bắc, Cường dựng cố định một cây sào thẳng đứng rồi đánh dấu chiều cao của các bạn lên đó bởi ba điểm. Cường đặt tên các điểm đó theo thứ tự từ dưới lên là A, B, C và giải thích rằng điểm A ứng với chiều cao của bạn An, B ứng với chiều cao bạn Bắc và C ứng với chiều cao của Cường. Biết rằng bạn An cao 150cm, bạn Bắc cao 153cm, bạn Cường cao 148cm. Theo em, Cường giải thích như thế có đúng không? Nếu không thì phải sửa như nào cho đúng?
Phương pháp giải:
So sánh chiều cao của các bạn rồi sắp xếp theo thứ tự tăng dần để rút ra nhận xét.
Lời giải:
Cường giải thích như thế là không đúng.
Vì cách đặt tên các điểm được đánh dấu tương tự như việc đặt tên các điểm trên tia số.
Chiều cao của các bạn theo thứ tự tăng dần là 148cm, 150cm, 153cm ứng với chiều cao của Cường, An và Bắc
Do vậy cần đánh dấu các điểm theo thứ tự từ dưới lên là C, A, B
Tập hợp các số tự nhiên kí hiệu là , tập hợp các số tự nhiên khác 0 kí hiệu là .
Ta có:
N = { 0; 1; 2 ; 3 ; 4 ;......}
= {1 ; 2 ; 3 ; 4; ......}
Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Trên tia số, điểm biểu diễn số nhỏ ở bên trái điểm biểu diễn số lớn.
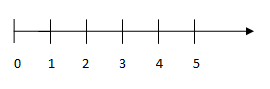
Số tự nhiên a được gọi là điểm a. Điểm 0 là gốc.
Ví dụ: Điểm biểu diễn số 4 trên tia số ta gọi là điểm 4.
2. Thứ tự trong tập hợp các số tự nhiên
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết hoặc
Ngoài ra ta cũng viết để chỉ hoặc
+ Nếu và thì (Tính chất bắc cầu)
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.
+ Số 0 là số tự nhiên bé nhất.
Ví dụ:
Số 3 và số 4 là hai số tự nhiên liên tiếp. Số liền sau của 8 là 9.
Số liền trước của 6 là 5.
Các dạng bài tập
1. Tìm số liền sau, số liền trước của một số tự nhiên cho trước
Phương pháp:
- Để tìm số liền sau của số tự nhiên ta tính
- Để tìm số liền trước của số tự nhiên khác ta tính
Chú ý:
- Số không có số liền trước.
- Hai số tự nhiên liên tiếp thì hơn kém nhau đơn vị.
2. Tìm các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp:
Liệt kê tất cả các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho
Ví dụ:
Tìm tất cả các số tự nhiên thỏa mãn
Giải:
Ta có: các số tự nhiên lớn hơn và nhỏ hơn là: .
Tìm tất cả các số tự nhiên thỏa mãn
3. Sử dụng công thức đếm số các số tự nhiên
Phương pháp:
Để đếm các số tự nhiên từ đến hai số liên tiếp cách nhau đơn vị, ta dùng công thức sau:
hay bằng (số cuối – số đầu):khoảng cách +1.
- Căn cứ vào các phần tử đã được liệt kê hoặc căn cứ vào tính chất đặc trưng cho các phần tử của tập hợp cho trước, ta có thể tìm được số phần tử của tập hợp đó.
- Sử dụng các công thức sau:
+ Tập hợp các số tự nhiên từ đến có: phần tử (1)
+ Tập hợp các số chẵn từ số chẵn đến số chẵn có: phần tử ( 2)
+ Tập hợp các số lẻ từ số lẻ đến số lẻ có: phần tử ( 3)
+ Tập hợp các số tự nhiên từ đến hai số kế tiếp cách nhau d đơn vị, có: phần tử (4)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
