Với giải Bài 9.44 trang 111 Toán 8 Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối chương 9 trang 110 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Bài 9.44 trang 111 Toán 8 Tập 2 | Kết nối tri thức Giải Toán lớp 8
Bài 9.44 trang 111 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 4 cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB.
a) Chứng minh rằng ΔHDA ∽ ΔAHC .
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD.
Lời giải:
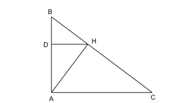
a) Ta có (do tam giác ACH vuông ở H).
Suy ra (cùng phụ với ).
Tam giác HDA vuông tại D và tam giác AHC vuông tại H có nên ΔHDA ∽ ΔAHC .
b) Áp dụng định lí Pythagore cho tam giác vuông ABC, ta có
BC2 = AB2 + AC2 = 42 + 52 = 41.
Suy ra cm.
Diện tích tam giác ABC là: (cm2).
Lại có , do đó AH ∙ BC = 2 . 10 = 20, suy ra AH = =(cm).
Áp dụng định lí Pythagore cho tam giác ACH ta có AC2 = AH2 + CH2.
Do đó, CH2 = AC2 – AH2 = 42 – .
Suy ra (cm).
Vì ΔHDA ∽ ΔAHC nên (cm).
Ta có BH = BC – HC = (cm).
Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 9.37 trang 110 Toán 8 Tập 2: Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽ ΔABC. Khẳng định nào sau đây là đúng?
Bài 9.38 trang 110 Toán 8 Tập 2: Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng?
Bài 9.39 trang 110 Toán 8 Tập 2: Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?
Bài 9.40 trang 110 Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB ≠ AC) và tam giác DEF vuông tại D (DE ≠ DF). Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF?
Bài 9.41 trang 110 Toán 8 Tập 2: Cho Hình 9.73, biết rằng MN // AB, MP // AC. Hãy liệt kê ba cặp hai tam giác (khác nhau) đồng dạng có trong hình.
Bài 9.42 trang 110 Toán 8 Tập 2: Cho Hình 9.74, biết rằng . Chứng minh rằng ΔABD ∽ ΔACE và ΔBOE ∽ ΔCOD.
Bài 9.43 trang 110 Toán 8 Tập 2:Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.
Bài 9.44 trang 111 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 4 cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB.
Bài 9.45 trang 111 Toán 8 Tập 2: Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt là trung điểm của AH, BH (H.9.76).
Bài 9.46 trang 111 Toán 8 Tập 2: Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC. Chứng minh rằng:
Bài 9.47 trang 111 Toán 8 Tập 2: Để tính được chiều cao gần đúng của kim tự tháp Ai Cập, người ta cắm một cây cọc cao 1 m vuông góc với mặt đất và đo được bóng cây cọc trên mặt đất là 1,5 m.
Bài 9.48 trang 111 Toán 8 Tập 2: Từ căn hộ chung cư nhà mình, bạn Lan đứng cách cửa sổ 1 m nhìn sang tòa nhà đối diện thì vừa nhìn thấy đúng tất cả 6 tầng của tòa nhà đó.
Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác: