Với Giải Bài 30 trang 100 SBT Toán 11 Tập 2 trong Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện Sách bài tập Toán lớp 11 Cánh Diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.
Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo của các góc nhị diện [A, SO, B]
Bài 30 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo của các góc nhị diện [A, SO, B] và [B, SO, C]. Tính α + β.
Lời giải:
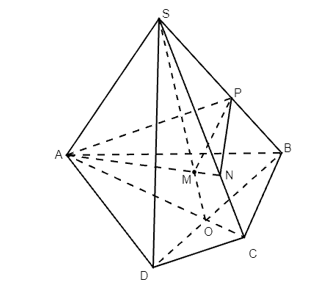
Trong (SAC): Kẻ AN ⊥ SO (N ∈ SC), gọi M = AN ∩ SO (M ∈ SO).
Trong (SOB): Kẻ PM ⊥ SO tại M (P ∈ SB).
· Ta có: AM ⊥ SO, PM ⊥ SO và AM ∩ PM = M ∈ SO.
Suy ra là góc phẳng nhị diện của góc nhị diện [A, SO, B], tức là
· Lại có: NM ⊥ SO, PM ⊥ SO và NM ∩ PM = M ∈ SO.
Suy ra là góc phẳng nhị diện của góc nhị diện [B, SO, C], tức là
Suy ra:
Trong (APN) có: M ∈ AN nên 3 điểm A, M, N thẳng hàng, do đó
Từ đó ta có: α + β = 180°.
Xem thêm các bài giải Toán 11 Cánh Diều hay, chi tiết khác:
Bài 24 trang 99 SBT Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau, đường thẳng d cắt (P) sao cho góc giữa đường thẳng d và mặt phẳng (P) bằng φ (0° < φ < 90°). Khi đó, góc giữa đường thẳng d và mặt phẳng (Q) bằng:
Bài 25 trang 99 SBT Toán 11 Tập 2: Cho hai đường thẳng a và b song song với nhau, mặt phẳng (P) cắt a sao cho góc giữa đường thẳng a và mặt phẳng (P) bằng φ (0° < φ < 90°). Khi đó, góc giữa đường thẳng b và mặt phẳng (P) bằng:
Bài 26 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi I là hình chiếu của A trên đường thẳng BC, α là góc giữa đường thẳng SI và mặt phẳng (ABC), β là số đo nhị diện [S, BC, A]. Phát biểu nào sau đây đúng?
Bài 27 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a. Gọi α, β, γ lần lượt là số đo của các góc nhị diện [B, SA, C], [A, BC, S], [A, SC, B]. Tính:
Bài 29 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), ABCD là hình thoi cạnh a, AC = a, Tính số đo của góc nhị diện [S, CD, A].
Bài 30 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo của các góc nhị diện [A, SO, B] và [B, SO, C]. Tính α + β.
Bài 31 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. Gọi α1, α2, α3, α4 lần lượt là góc giữa các đường thẳng SA, SB, SC, SD và mặt phẳng (ABCD). Chứng minh rằng:
Bài 32 trang 100 SBT Toán 11 Tập 2: Một máy nước nóng sử dụng năng lượng mặt trời như ở hình 20 có các ống hấp nhiệt chân không dài 1,8 m được đặt trên sân thượng của một toà nhà. Khi tia nắng mặt trời chiếu vuông góc với sân thượng, bóng nắng của các ống hấp nhiệt chân không lên mặt sân dài 1,2 m. Các ống hấp nhiệt chân không đó tạo với mặt sân thượng một góc bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?