Toán 11 (Kết nối tri thức) Bài tập cuối chương 7

Trần Thị Thùy Linh Ngày: 27-01-2024 Lớp 11

248

Toptailieu biên soạn và giới thiệu lời giải Toán 11 (Kết nối tri thức) Bài 11: Vị trí địa lí, điều kiện tự nhiên, dân cư, xã hội và kinh tế khu vực Đông Nam Á hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài tập cuối chương 7 từ đó học tốt môn Toán 11.

Toán 11 (Kết nối tri thức) Bài tập cuối chương 7

Trắc nghiệm

Giải Toán 11 trang 64 Tập 2

Bài 7.33 trang 64 Toán 11 Tập 2: Cho các phát biểu sau:

(1) (P) và (Q) có giao tuyến là đường thẳng a và cùng vuông góc với mặt phẳng (R) thì a $⊥$ (R).

(2) Hai mặt phẳng (P) và (Q) vuông góc với nhau và có giao tuyến là đường thẳng a, một đường thẳng b nằm trong mặt phẳng (P) và vuông góc với đường thẳng a thì b $⊥$ (Q).

(3) Mặt phẳng (P) chứa đường thẳng a và a vuông góc với (Q) thì (P) $⊥$ (Q).

(4) Đường thẳng a nằm trong mặt phẳng (P) và mặt phẳng (P) vuông góc với mặt phẳng (Q) thì a $⊥$ (Q).

Số phát biểu đúng trong các phát biểu trên là:

Lời giải:

Đáp án đúng là: C

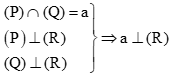
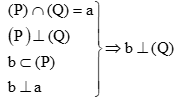
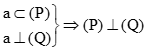
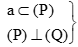
+) Bài 7.33 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 nên (1) đúng.

+) Bài 7.33 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 nên (2) đúng.

+) Bài 7.33 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 nên (3) đúng.

+) Bài 7.33 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 ta chưa kết luận được a $⊥$ (Q) vì có thể xảy ra trường hợp song song nên (4) sai.

Bài 7.34 trang 64 Toán 11 Tập 2: Cho mặt phẳng (P) vuông góc với mặt phẳng (Q) và a là giao tuyến của (P) và (Q). Trong các phát biểu dưới đây, phát biểu nào đúng?

A. Đường thẳng d nằm trên (Q) thì d vuông góc với (P).

B. Đường thẳng d nằm trên (Q) và d vuông góc với a thì d vuông góc với (P).

C. Đường thẳng d vuông góc với a thì d vuông góc với (P).

D. Đường thẳng d vuông góc với (Q) thì d vuông góc với (P).

Lời giải:

Đáp án đúng là: B

Bài 7.34 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Bài 7.35 trang 64 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng?

A. Số đo của góc nhị diện [S, AB, C] bằng $\hat{S B C}$ .

B. Số đo của góc nhị diện [D, SA, B] bằng 90°.

C. Số đo của góc nhị diện [S, AC, B] bằng 90°.

D. Số đo của góc nhị diện [D, SA, B] bằng $\hat{B S D}$ .

Lời giải:

Đáp án đúng là: C

Bài 7.35 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Gọi O là giao điểm của AC và BD. Kẻ OE $⊥$ AB tại E.

Do ABCD là hình vuông nên O là trung điểm của AC và BD.

Xét tam giác ABD có OE // AD (do cùng vuông góc với AB) mà O là trung điểm của BD nên E là trung điểm của AB.

Xét tam giác SAB có SA = SB (do S.ABCD là hình chóp tứ giác đều) nên SAB là tam giác cân tại S mà SE là trung tuyến nên SE đồng thời là đường cao hay SE $⊥$ AB.

Do đó [S, AB, C] = $\hat{S E O}$ , suy ra A sai.

Vì ABCD là hình vuông nên BO $⊥$ AC, S.ABCD là hình chóp đều nên SO $⊥$ (ABCD) suy ra SO $⊥$ AC, SO $⊥$ BD .

Vì BO $⊥$ AC, SO $⊥$ AC nên [S, AC, B] = $\hat{S O B}$ = 90^o, suy ra C đúng.

Kẻ DF $⊥$ SA tại F.

Vì SO $⊥$ BD và AC $⊥$ BD nên BD $⊥$ (SAC), suy ra BD $⊥$ SA mà DF $⊥$ SA nên SA $⊥$ (BDF), suy ra SA $⊥$ BF.

Vì SA $⊥$ BF và DF $⊥$ SA nên [D, SA, B] = $\hat{B F D}$ , suy ra B, D sai.

Bài 7.36 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA $⊥$ (ABCD).

Phát biểu nào sau đây là sai?

A. Đường thẳng BC vuông góc với mặt phẳng (SAB).

B. Đường thẳng BD vuông góc với mặt phẳng (SAC).

C. Đường thẳng AC vuông góc với mặt phẳng (SBD).

D. Đường thẳng AD vuông góc với mặt phẳng (SAB).

Lời giải:

Đáp án đúng là: C

Bài 7.36 trang 64 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Vì ABCD là hình vuông nên AB $⊥$ BC mà SA $⊥$ (ABCD) nên SA $⊥$ BC.

Có AB $⊥$ BC và SA $⊥$ BC nên BC $⊥$ (SAB). Vậy A đúng.

Vì ABCD là hình vuông nên AC $⊥$ BD mà SA $⊥$ (ABCD) nên SA $⊥$ BD.

Có AC $⊥$ BD và SA $⊥$ BD nên BD $⊥$ (SAC). Vậy B đúng.

Vì ABCD là hình vuông nên AD $⊥$ AB mà SA $⊥$ (ABCD) nên SA $⊥$ AD.

Có AD $⊥$ AB và SA $⊥$ AD nên AD $⊥$ (SAB). Vậy D đúng.

Bài 7.37 trang 64 Toán 11 Tập 2: Thể tích của khối chóp có diện tích đáy bằng S, chiều cao bằng h là:

A. V = S ∙ h.

B. V = $\frac{1}{2}$ .S.h.

C. V = $\frac{1}{3}$ .S.h.

D. V = $\frac{2}{3}$ .S.h.

Lời giải:

Đáp án đúng là: C

Ta có thể tích khối chóp là V = $\frac{1}{3}$ .S.h.

Tự luận

Giải Toán 11 trang 65 Tập 2

Bài 7.38 trang 65 Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = a $\sqrt{2}$ và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.

Lời giải:

Bài 7.38 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Kẻ OD $⊥$ BC tại D.

Có OA $⊥$ OB, OA $⊥$ OC nên OA $⊥$ (OBC), suy ra OA $⊥$ BC mà OD $⊥$ BC nên

BC $⊥$ (OAD).

Kẻ OE $⊥$ AD tại E.

Vì BC $⊥$ (OAD) nên BC $⊥$ OE mà OE $⊥$ AD nên OE $⊥$ (ABC).

Do đó d(O, (ABC)) = OE.

Xét tam giác OBC vuông tại O, OD là đường cao có:

$\frac{1}{O D^{2}} = \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ $= \frac{1}{2 a^{2}} + \frac{1}{4 a^{2}} = \frac{3}{4 a^{2}}$ .

Vì OA $⊥$ (OBC) nên OA $⊥$ OD.

Xét tam giác AOD vuông tại O, OE là đường cao nên

$\frac{1}{O E^{2}} = \frac{1}{O A^{2}} + \frac{1}{O D^{2}}$ $= \frac{1}{a^{2}} + \frac{3}{4 a^{2}} = \frac{7}{4 a^{2}}$ $\Rightarrow O E = \frac{2 a \sqrt{7}}{7}$ .

Vậy d(O, (ABC)) $= \frac{2 a \sqrt{7}}{7}$ .

Bài 7.39 trang 65 Toán 11 Tập 2: Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC.

a) Chứng minh rằng BC $⊥$ (AID).

b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng AH $⊥$ (BCD).

c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.

Lời giải:

Bài 7.39 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Vì tam giác ABC cân tại A, AI là trung tuyến nên AI đồng thời là đường cao hay AI $⊥$ BC.

Vì tam giác BCD cân tại D, DI là trung tuyến nên DI đồng thời là đường cao hay DI $⊥$ BC.

Có AI $⊥$ BC và DI $⊥$ BC nên BC $⊥$ (AID).

b) Do AH là đường cao của tam giác AID nên AH $⊥$ DI.

Vì BC $⊥$ (AID) nên BC $⊥$ AH mà AH $⊥$ DI nên AH $⊥$ (BCD).

c) Vì BC $⊥$ (AID) nên BC $⊥$ IJ, mà IJ là đường cao của tam giác AID nên IJ $⊥$ AD. Do đó IJ là đường vuông góc chung của AD và BC.

Bài 7.40 trang 65 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a và $\hat{C A B}$ = 30^o. Biết SA $⊥$ (ABC) và SA = a $\sqrt{2}$ .

a) Chứng minh rằng (SBC) $⊥$ (SAB).

b) Tính theo a khoảng cách từ điểm A đến đường thẳng SC và khoảng cách từ điểm A đến mặt phẳng (SBC).

Lời giải:

Bài 7.40 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Do tam giác ABC vuông tại B nên AB $⊥$ BC.

Vì SA $⊥$ (ABC) nên SA $⊥$ BC mà AB $⊥$ BC nên BC $⊥$ (SAB), suy ra (SBC) $⊥$ (SAB).

b) Kẻ AD $⊥$ SC tại D. Khi đó d(A, SC) = AD.

Vì SA $⊥$ (ABC) nên SA $⊥$ AC nên tam giác SAC vuông tại A.

Xét tam giác ABC vuông tại B, sin $\hat{C A B}$ = $\frac{B C}{A C}$

$\Rightarrow$ AC = $\frac{B C}{\sin \hat{C A B}} = \frac{a}{\sin 30 °}$ = 2a.

Xét tam giác SAC vuông tại A, AD là đường cao, có:

$\frac{1}{A D^{2}} = \frac{1}{S A^{2}} + \frac{1}{A C^{2}}$ $= \frac{1}{2 a^{2}} + \frac{1}{4 a^{2}} = \frac{3}{4 a^{2}}$ $\Rightarrow A D = \frac{2 a \sqrt{3}}{3}$ .

Vậy d(A, SC) $= \frac{2 a \sqrt{3}}{3}$ .

Kẻ AE $⊥$ SB tại E.

Vì BC $⊥$ (SAB) nên BC $⊥$ AE mà AE $⊥$ SB nên AE $⊥$ (SBC).

Khi đó d(A, (SBC)) = AE.

Xét tam giác ABC vuông tại B, có AB = $\frac{B C}{\tan 30 °} = \frac{a}{\tan 30 °}$ = a $\sqrt{3}$ .

Vì SA $⊥$ (ABC) nên SA $⊥$ AB, suy ra tam giác SAB vuông tại A.

Xét tam giác SAB vuông tại A, AE là đường cao, có: $\frac{1}{A E^{2}} = \frac{1}{S A^{2}} + \frac{1}{A B^{2}}$ .

$= \frac{1}{2 a^{2}} + \frac{1}{3 a^{2}} = \frac{5}{6 a^{2}}$ $\Rightarrow$ AE = a $\sqrt{\frac{6}{5}}$

Vậy d(A, (SBC)) = a $\sqrt{\frac{6}{5}}$ .

Bài 7.41 trang 65 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) $⊥$ (ABCD).

a) Tính theo a thể tích của khối chóp S.ABCD.

b) Tính khoảng cách giữa hai đường thẳng AD và SC.

Lời giải:

Bài 7.41 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Kẻ SE $⊥$ AD tại E. Vì tam giác SAD vuông cân tại S nên E là trung điểm của AD.

Có (SAD) $⊥$ (ABCD), (SAD) $\cap$ (ABCD) = AD, SE $⊥$ AD nên SE $⊥$ (ABCD).

Vì tam giác SAD vuông cân tại S, SE là trung tuyến nên SE = $\frac{A D}{2} = \frac{a}{2}$ .

Khi đó $V_{S . A B C D} = \frac{1}{3} S_{A B C D} \cdot S E$ $= \frac{1}{3} \cdot a^{2} \cdot \frac{a}{2} = \frac{a^{3}}{6}$ .

b) Do ABCD là hình vuông nên AD // BC mà BC $\subset$ (SBC) nên AD // (SBC).

Khi đó d(AD, SC) = d(AD, (SBC)) = d(E, (SBC)).

Kẻ EF // AB (F thuộc BC). Khi đó EF $⊥$ BC (vì AB $⊥$ BC).

Mà SE $⊥$ (ABCD) nên SE $⊥$ BC mà EF $⊥$ BC nên BC $⊥$ (SEF).

Lại có BC $\subset$ (SBC) nên (SBC) $⊥$ (SEF) và (SBC) $\cap$ (SEF) = SF.

Kẻ EG $⊥$ SF tại G nên EG $⊥$ (SBC). Khi đó d(E, (SBC)) = EG.

Do ABCD là hình vuông nên EF = AB = a.

Xét tam giác SEF vuông tại E, EG là đường cao, có

$\frac{1}{E G^{2}} = \frac{1}{S E^{2}} + \frac{1}{E F^{2}}$ $= \frac{4}{a^{2}} + \frac{1}{a^{2}} = \frac{5}{a^{2}}$ $\Rightarrow$ EG = $\frac{a}{\sqrt{5}}$ .

Vậy d(AD, SC) = $\frac{a}{\sqrt{5}}$ .

Bài 7.42 trang 65 Toán 11 Tập 2: Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a, AA' $⊥$ (ABCD) và $\hat{B A D}$ = 60^o.

a) Tính thể tích của khối hộp ABCD.A'B'C'D'.

b) Tính khoảng cách từ A đến mặt phẳng (A'BD).

Lời giải:

Bài 7.42 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Gọi O là giao điểm của AC và BD.

Vì hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a nên ABCD là hình thoi, suy ra AO = OC và AC $⊥$ BD.

Có S_ABD= $\frac{1}{2}$ .AO.BD = $\frac{1}{2}$ .CO.BD = S_BCD. Do đó S_ABCD = 2S_ABD.

Mà S_ABD= $\frac{1}{2}$ .AB.AD.sin $\hat{B A D}$ = $\frac{1}{2}$ .a.a.sin60^o = $\frac{a^{2} \sqrt{3}}{4}$ . Do đó S_ABCD = $\frac{a^{2} \sqrt{3}}{2}$ .

Vậy $V_{A B C D . A^{'} B' C^{'} D^{'}} = A A^{'} \cdot S_{A B C D}$ $= a \cdot \frac{a^{2} \sqrt{3}}{2} = \frac{a^{3} \sqrt{3}}{2}$ .

b) Vì AO $⊥$ BD mà AA' $⊥$ (ABCD) nên AA' $⊥$ BD. Do đó BD $⊥$ (AOA').

Suy ra (A'BD) $⊥$ (AOA').

Kẻ AE $⊥$ A'O tại E. Vì (A'BD) $⊥$ (AOA'), (A'BD) $\cap$ (AOA') = A'O và AE $⊥$ A'O nên AE $⊥$ (A'BD). Do đó d(A, (A'BD)) = AE.

Xét tam giác ABD có AB = AD = a nên tam giác ABD là tam giác cân tại A mà $\hat{B A D} = 60^{o}$ nên tam giác ABD đều, suy ra BD = a mà BO = $\frac{B D}{2} = \frac{a}{2}$ .

Xét tam giác AOB vuông tại O, có AO = $\sqrt{A B^{2} - B O^{2}}$ = $\sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a \sqrt{3}}{2}$ .

Vì AA' $⊥$ (ABCD) nên AA' $⊥$ AO hay tam giác A'AO vuông tại A.

Xét tam giác A'AO vuông tại A có $\frac{1}{A E^{2}} = \frac{1}{A {A^{'}}^{2}} + \frac{1}{A O^{2}}$ $= \frac{1}{a^{2}} + \frac{4}{3 a^{2}} = \frac{7}{3 a^{2}}$

$\Rightarrow A E = a \sqrt{\frac{3}{7}}$ .

Vậy d(A, (A'BD)) = $a \sqrt{\frac{3}{7}}$ .

Bài 7.43 trang 65 Toán 1 Tập 2: Cho hình lăng trụ ABCD.A'B'C'D'. Biết A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a. Tính theo a thể tích của khối lăng trụ ABCD.A'B'C'D' và thể tích của khối chóp A'.BB'C'C.

Lời giải:

Bài 7.43 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Gọi O là giao điểm của AC và BD.

Do A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a nên A'O $⊥$ (ABCD).

Vì ABCD là hình vuông cạnh a nên S_ABCD = a².

Xét tam giác ABC vuông tại B, có AC = $\sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ mà O là trung điểm của AC nên AO = $\frac{A C}{2} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác A'AO vuông tại O, có A'O = $\sqrt{A^{'} A^{2} - A O^{2}} = \sqrt{a^{2} - \frac{a^{2}}{2}} = \frac{a \sqrt{2}}{2}$ .

Khi đó $V_{A B C D . A^{'} B^{'} C^{'} D^{'}} = A^{'} O \cdot S_{A B C D} = \frac{a \sqrt{2}}{2} \cdot a^{2} = \frac{a^{3} \sqrt{2}}{2}$ .

Ta có $V_{A B C D . A^{'} B^{'} C^{'} D^{'}} = V_{A A^{'} D^{'} D . B B^{'} C^{'} C} = \frac{a^{3} \sqrt{2}}{2}$ .

Khi đó ta thấy khối chóp A'.BB'C'C và khối lăng trụ AA'D'D.BB'C'C có chung đường cao và đáy nên $V_{A^{'} . B B^{'} C^{'} C} = \frac{1}{3} \cdot V_{A A^{'} D^{'} D . B B^{'} C^{'} C} = \frac{1}{3} \cdot \frac{a^{3} \sqrt{2}}{2} = \frac{a^{3} \sqrt{2}}{6}$ .

Bài 7.44 trang 65 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD và AB = BC = DA = a, CD = 2a. Biết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và SA = a $\sqrt{2}$ . Tính theo a khoảng cách từ S đến mặt phẳng (ABCD) và thể tích của khối chóp S.ABCD.

Lời giải:

Bài 7.44 trang 65 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Gọi O là giao điểm của AC và BD.

Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) nên SO $⊥$ (ABCD).

Khi đó d(S, (ABCD)) = SO.

Kẻ AH $⊥$ DC tại H, BK $⊥$ DC tại K.

Khi đó ABKH là hình chữ nhật nên AB = HK = a.

Xét $∆$ AHD và $∆$ BKC có: AD = BC = a, $\hat{A H D} = \hat{B K C} = 90 °$ , $\hat{A D H} = \hat{B C K}$ (do ABCD là hình thang cân).

Do đó $∆$ AHD = $∆$ BKC, suy ra DH = CK = $\frac{D C - H K}{2} = \frac{2 a - a}{2} = \frac{a}{2}$ ;

CH = HK + CK = a+ $\frac{a}{2} = \frac{3 a}{2}$ .

Xét tam giác AHD vuông tại H, có AH = $\sqrt{A D^{2} - D H^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a \sqrt{3}}{2}$ .

Xét tam giác AHC vuông tại H, có AC = $\sqrt{A H^{2} + H C^{2}} = \sqrt{\frac{3 a^{2}}{4} + \frac{9 a^{2}}{4}} = a \sqrt{3}$ .

Vì AB // CD nên $\frac{A O}{O C} = \frac{A B}{C D} \Rightarrow \frac{A O}{O C} = \frac{a}{2 a} = \frac{1}{2}$ $\Rightarrow A O = \frac{1}{3} A C = \frac{a \sqrt{3}}{3}$ .

Xét tam giác SOA vuông tại O, có SO = $\sqrt{S A^{2} - A O^{2}}$ $= \sqrt{2 a^{2} - \frac{a^{2}}{3}} = \frac{a \sqrt{15}}{3}$ .

Khi đó d(S, (ABCD)) $= \frac{a \sqrt{15}}{3}$ .

Ta có $S_{A B C D} = \frac{1}{2} \cdot (A B + C D) \cdot A H$ $= \frac{1}{2} \cdot (a + 2 a) \cdot \frac{a \sqrt{3}}{2}$ $= \frac{3 a^{2} \sqrt{3}}{4}$ .

Vậy $V_{S . A B C D} = \frac{1}{3} \cdot S_{A B C D} \cdot S O$ $= \frac{1}{3} \cdot \frac{3 a^{2} \sqrt{3}}{4} \cdot \frac{a \sqrt{15}}{3}$ $= \frac{a^{3} \sqrt{45}}{12}$ $= \frac{a^{3} \sqrt{5}}{4}$ .