Toptailieu biên soạn và giới thiệu lời giải Toán 11 (Kết nối tri thức) Bài 33: Đạo hàm cấp hai hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài 33 từ đó học tốt môn Toán 11.

Toán 11 (Kết nối tri thức) Bài 33: Đạo hàm cấp hai

Giải Toán 11 trang 95 Tập 2

Mở đầu trang 95 Toán 11 Tập 2: Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khí) được cho bởi phương trình sau:

x(t) = 4cos$\left(2\pi t+\frac{\pi }{3}\right)$,

ở đó x tính bằng centimet và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Vận tốc của vật tại thời điểm t là

v(t) = x'(t) = -$\left(2\pi t+\frac{\pi }{3}\right)$'.4sin$\left(2\pi t+\frac{\pi }{3}\right)$ = -8$\pi$sin$\left(2\pi t+\frac{\pi }{3}\right)$.

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = -8$\pi$$\left(2\pi t+\frac{\pi }{3}\right)$'.cos$\left(2\pi t+\frac{\pi }{3}\right)$ = -16${\pi }^2$cos$\left(2\pi t+\frac{\pi }{3}\right)$.

Tại thời điểm t = 5, gia tốc của vật là:

a(5) = $-16{\pi }^2\cos \left(2\pi .5+\frac{\pi }{3}\right)\approx -79$ (cm/s²).

1. Khái niệm đạo hàm cấp hai

HĐ1 trang 95 Toán 11 Tập 2: Nhận biết đạo hàm cấp hai của một hàm số

a) Gọi g(x) là đạo hàm của hàm số y = sin$\left(2x+\frac{\pi }{4}\right)$. Tìm g(x).

b) Tính đạo hàm của hàm số y = g(x).

Lời giải:

a) Ta có

g(x) = y' = 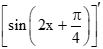= 2.cos$\left(2x+\frac{\pi }{4}\right)$.

b) Ta có

g'(x) =  = -4sin$\left(2x+\frac{\pi }{4}\right)$.

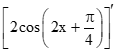
Luyện tập 1 trang 95 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = xe^2x;

b) y = ln(2x + 3).

Lời giải:

a) Ta có y = xe^2x

Suy ra: y' = x' . e^2x + x . (e^2x)' = e^2x + 2xe^2x.

Do đó, y'' = 2e^2x + 2(e^2x + 2xe^2x) = 2e^2x + 2e^2x + 4xe^2x = 4e^2x + 4xe^2x.

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = 4e^2x + 4xe^2x.

b) Ta có y = ln(2x + 3).

y' = $\frac{(2x+3{)}^{\text{'}}}{2x+3}=\frac{2}{2x+3}$ .

y'' = ${\left(\frac{2}{2x+3}\right)}^{\text{'}}=\frac{-2.2}{{\left(2x+3\right)}^2}=\frac{-4}{{\left(2x+3\right)}^2}$ .

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = $\frac{-4}{{\left(2x+3\right)}^2}$ .

2. Ý nghĩa cơ học của đạo hàm cấp hai

Giải Toán 11 trang 96 Tập 2

HĐ2 trang 96 Toán 11 Tập 2: Nhận biết ý nghĩa cơ học của đạo hàm cấp hai

Xét một chuyển động có phương trình s = 4cos2πt.

a) Tính vận tốc tức thời của chuyển động tại thời điểm t.

b) Tính gia tốc tức thời tại thời điểm t.

Lời giải:

a)

Ta có: v(t) = s'(t) = –4.2πsin2πt = –8πsin2πt.

Vậy vận tốc tức thời của chuyển động tại thời điểm t là –8πsin2πt.

b) Gia tốc tức thời tại thời điểm t là

a(t) = v'(t) = (–8πsin2πt)' = –8π.2πcos2πt = –16π²cos2πt.

Vận dụng trang 96 Toán 11 Tập 2: Một chuyển động thẳng có phương trình $s=2t^2+\frac{1}{2}{t}^4$ (s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.

Lời giải:

Vận tốc tại thời điểm t là v(t) = s'(t) = 4t + 2t³.

Gia tốc tức thời của vật tại thời điểm t là a(t) = v'(t) = 4 + 6t².

Tại thời điểm t = 4 giây, gia tốc của vật là:

a(4) = 4 + 6 . 4² = 100 (m/s²).

Bài tập

Bài 9.13 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = x²e^x. Tính f''(0).

Lời giải:

Với f(x) = x²e^x, ta có:

f'(x) = (x²)' . e^x + x² . (e^x)' = 2x.e^x + x².e^x.

f''(x) = (2e^x + 2x.e^x) + (2x.e^x + x².e^x) = 4xe^x + 2e^x + x²e^x.

Vậy f''(0) = 4 . 0 . e⁰ + 2 . e⁰ + 0² . e⁰ = 2.

Bài 9.14 trang 96 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = ln(x + 1);

b) y = tan2x.

Lời giải:

a) Ta có y' = (ln(x+1))' = $\frac{{\left(x+1\right)}^{\text{'}}}{x+1}=\frac{1}{x+1}$

$\Rightarrow {y^{\text{'}}}^{\text{'}}={\left(\frac{1}{x+1}\right)}^{\text{'}}=\frac{-1}{{\left(x+1\right)}^2}$.

b)

Ta có y' = (tan2x)' = $\frac{2}{{\cos }^{2}2x}$

$\Rightarrow {y^{\text{'}}}^{\text{'}}=\frac{-2{\left({\cos }^{2}2x\right)}^{\text{'}}}{{\cos }^{4}2x}=\frac{-2.2\cos 2x.(\cos 2x{)}^{\text{'}}}{{\cos }^{4}2x}$

$=\frac{4.2\sin 2x}{{\cos }^{3}2x}=\frac{8\sin 2x}{{\cos }^{3}2x}$.

Bài 9.15 trang 96 Toán 11 Tập 2: Cho hàm số P(x) = ax² + bx + 3 (a, b là hằng số). Tìm a, b biết P'(1) = 0 và P''(1) = –2.

Lời giải:

Ta có:

P'(x) = 2ax + b

P''(x) = 2a

Do P'(1) = 0 và P''(1) = –2 nên ta có

Vậy a = – 1 và b = 2.

Bài 9.16 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = $2{\sin }^2\left(x+\frac{\pi }{4}\right)$ . Chứng minh rằng |f''(x)| ≤ 4 với mọi x.

Lời giải:

Ta có:

$f^{\text{'}}\left(x\right)=2.2\sin \left(x+\frac{\pi }{4}\right)$.

$=4\sin \left(x+\frac{\pi }{4}\right)\cos \left(x+\frac{\pi }{4}\right)=2\sin \left(2x+\frac{\pi }{2}\right)$

Khi đó ${f^{\text{'}}}^{\text{'}}\left(x\right)=2.{\left(2x+\frac{\pi }{2}\right)}^{\text{'}}.\cos \left(2x+\frac{\pi }{2}\right)=4\cos \left(2x+\frac{\pi }{2}\right)$ .

Vì  với mọi x nên 4 $\le$4 với mọi x.

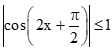
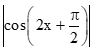
Vậy |f''(x)| ≤ 4 với mọi x.

Bài 9.17 trang 96 Toán 11 Tập 2: Phương trình chuyển động của một hạt được cho bởi s(t) = 10 + 0,5sin$\left(2\pi t+\frac{\pi }{5}\right)$, trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Vận tốc tại thời điểm t là:

v(t) = s'(t) = 0,5.2πcos$\left(2\pi t+\frac{\pi }{5}\right)$= πcos$\left(2\pi t+\frac{\pi }{5}\right)$.

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = –π.2πsin$\left(2\pi t+\frac{\pi }{5}\right)$= –2π²sin$\left(2\pi t+\frac{\pi }{5}\right)$.

Tại thời điểm t = 5 giây, gia tốc của vật là:

a(5) = –2π²sin$\left(2\pi t+\frac{\pi }{5}\right)$ ≈ –11,6 (cm/s²).

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 32: Các quy tắc tính đạo hàm

Bài tập cuối chương 9 trang 97

Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit

Hoạt động thực hành trải nghiệm Hình học

Bài tập ôn tập cuối năm