Toptailieu.vn xin giới thiệu Lý thuyết Hàm số mũ. Hàm số lôgarit (Chân trời sáng tạo) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Hàm số mũ. Hàm số lôgarit (Chân trời sáng tạo) hay, chi tiết | Lý thuyết Toán 11
A. Lý thuyết Hàm số mũ. Hàm số lôgarit
1. Hàm số mũ
- Hàm số được gọi là hàm số mũ cơ số a.
- Hàm số có:
+ Tập xác định: .
+ Tập giá trị: .
+ Hàm số liên tục trên .
+ Sự biến thiên:
+ Đồ thị:
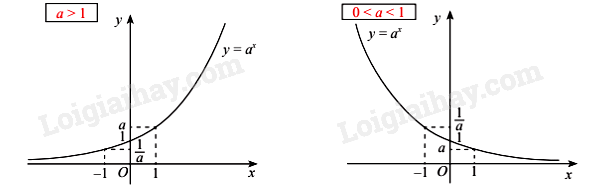
2. Hàm số lôgarit
- Hàm số được gọi là hàm số lôgarit cơ số a.
- Hàm số có:
+ Tập xác định: .
+ Tập giá trị: .
+ Hàm số liên tục trên .
+ Sự biến thiên:
+ Đồ thị:
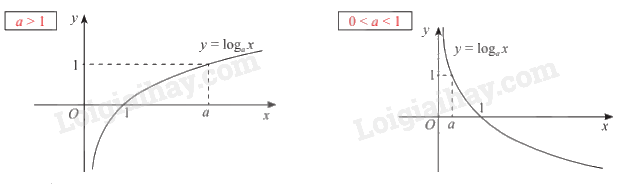
Sơ đồ tư duy Hàm số mũ. Hàm số lôgarit
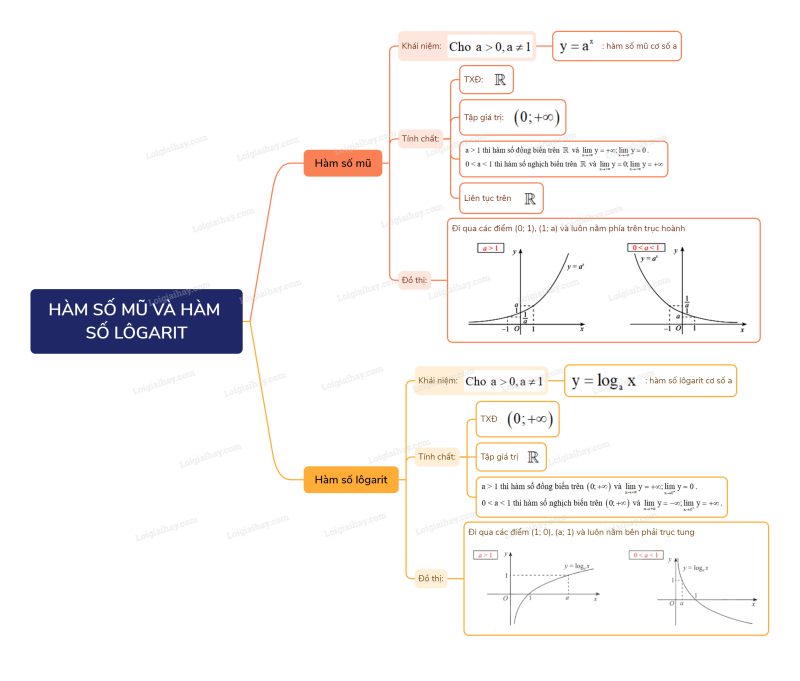
B. Bài tập Hàm số mũ. Hàm số lôgarit
Đang cập nhật ...
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.