Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Cánh diều) Bài 1: Tính đơn điệu của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 1 từ đó học tốt môn Toán 12.
Nội dung bài viết
Toán 12 (Cánh diều) Bài 1: Tính đơn điệu của hàm số
b) Cho hàm số y=f(x)=x2 có đồ thị như Hình 2.
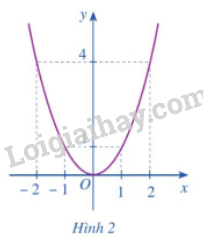
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Hoàn thành bảng biến thiên sau:
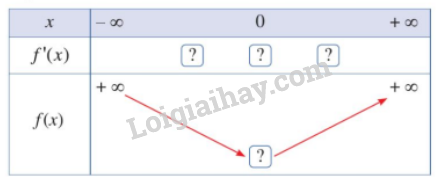
Lời giải:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và f(x) là hàm số xác định trên K.
- Hàm số f(x) được gọi là hàm số đồng biến trên K nếu với mọi x1,x2 thuộc K và x1<x2 thì f(x1)<f(x2).
- Hàm số f(x) được gọi là hàm số đồng biến trên K nếu với mọi x1,x2 thuộc K và x1<x2 thì f(x1)>f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
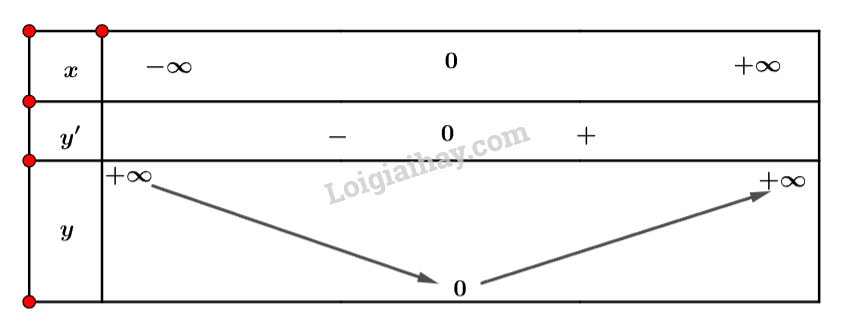
- Hàm số đồng biến trên khoảng (0;+∞) và nghịch biến trên khoảng (−∞;0).
- Đạo hàm f′(x)=2xâm khi x<0 và dương khi x>0.
- Hàm số y=f(x)=x2 nghịch biến khi f′(x)=2xmang dấu âm và đồng biến khi f′(x)=2x mang dấu dương.
- Ta có bàng biến thiên sau:
Lời giải:
Tập xác định D=R.
Ta có: y′=4x2−4x+1.
Xét y′=0⇔x=12.

Vậy hàm số đồng biến trên R.
Luyện tập 2 trang 7 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số y=x4+2x2−3.
Lời giải:
Tập xác định D=R.
Ta có: y′=4x3+4x.
Xét y′=0⇔x=0.
Ta có bảng biến thiên:

Vậy hàm số đồng biến trên khoảng (0;+∞) và nghịch biến trên khoảng (−∞;0).
Hoạt động 2 trang 7 SGK Toán 12 Tập 1: a) Xác định tính đồng biến, nghịch biến của hàm số f(x)=x3.
b) Xét dấu của đạo hàm f′(x)=3x2.
c) Phương trình f′(x)=0 có bao nhiêu nghiệm ?
Lời giải:
a) Tập xác định D=R.
Ta có: y′=3x2.
Xét y′=0⇒x=0.
Bảng biến thiên:
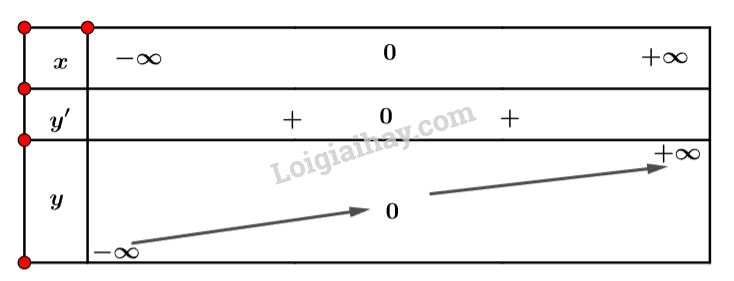
Vậy hàm số đồng biến trên R.
b) Dựa vào bảng biến thiên ta thấy đạo hàm y′=3x2 luôn dương với mọi x.
c) Phương trình f′(x)=0 có một nghiệm.
Lời giải:
Tập xác định D=R.
Ta có: y′=x√x2+1.
Xét y′=0⇔x=0.
Ta có bảng biến thiên:

Vậy hàm số y=√x2+1 nghịch biến trên nửa khoảng (−∞;0] và đồng biến trên nửa khoảng [0;+∞).
Luyện tập 4 trang 8 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số sau y=2x−1x+2.
Lời giải:
Tập xác định D=R∖{−2}.
Ta có: y′=5(x+2)2.
Nhận xét: y′>0 với mọi x∈D.
Ta có bảng biến thiên:

Vậy hàm số đồng biến trên mỗi khoảng (−∞;−2) và (−2;+∞).
Hoạt động 3 trang 9 SGK Toán 12 Tập 1: Dựa vào đồ thị hàm số y=f(x)=−x3−3x2+3 ở Hình 3, hãy so sánh:
a) f(−2) với mỗi giá trị f(x), ở đó x∈(−3;−1) và x≠−2.
b) f(0)với mỗi giá trị f(x), ở đó x∈(−1;1) và x≠0.

Lời giải:
a) Nhận xét: Ta thấy rằng f(x)>f(−2) với mọi x∈(−3;−1) và x≠−2.
b) Tương tự: Ta thấy rằng f(x)<f(0) với mọi x∈(−1;1) và x≠0.
Hoạt động 4 trang 10 SGK Toán 12 Tập 1: Quan sát bảng biến thiên dưới đây và cho biết:
a) xo có là điểm cực đại của hàm số f(x) hay không.
b) x1 có là điểm cực tiểu của hàm số h(x) hay không.

Lời giải:
a) xo có là điểm cực đại của hàm số f(x) .
b) x1 có là điểm cực tiểu của hàm số h(x).
Luyện tập 5 trang 11 SGK Toán 12 Tập 1: Tìm điểm cực trị của mỗi hàm số sau:
Lời giải:
a) Tập xác định: D=R.
Ta có: y′=4x3−12x+8.
Xét y′=0⇔[x=−2x=1
Ta có bảng biến thiên sau:
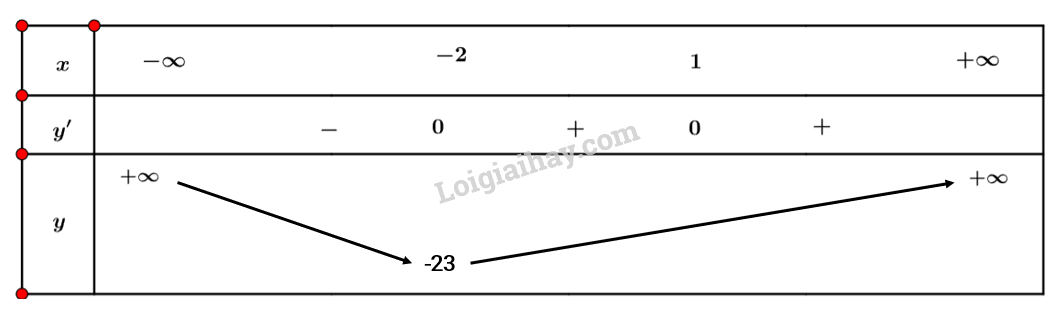
Vậy hàm số đạt cực đại tại điểm x=−2.
b) Tập xác định: D=R∖{1}.
Ta có: y′=−8(x−1)2.
Nhận xét y′<0∀x∈D
Ta có bảng biến thiên sau:

Vậy hàm số không có điểm cực trị.
Bài 1 trang 13 SGK Toán 12 Tập 1: Cho hàm số y=f(x)có bảng biến thiên như sau:
 Hàm số đồng biến trên khoảng nào dưới đây?
Hàm số đồng biến trên khoảng nào dưới đây?
A. (1;+∞).
B. (−1;0).
C. (−1;1).
D. (0;1).
Lời giải:
Dựa vào bảng biến thiên ta thấy đồ thị hàm số đi lên trong khoảng (0;1) nên hàm số đồng biến trên khoảng (0;1)⇒D.
Bài 2 trang 13 SGK Toán 12 Tập 1: Cho hàm số y=f(x)có bảng biến thiên như sau:
 Giá trị cực tiểu của hàm số đã cho bằng:
Giá trị cực tiểu của hàm số đã cho bằng:
a) 2.
b) 3.
c) −4.
d) 0.
Lời giải:
Giá trị cực tiểu của hàm số là y=−4⇒C
a) y=−x3+2x2−3 b) y=x4−2x2+5
c) y=3x+12−x d) y=x2−2xx+1
Lời giải:
a) Tập xác định: D=R.
Ta có: y′=−3x2+4x.
Nhận xét y′=0⇔[x=0x=43
Ta có bảng biến thiên sau:

Vậy hàm số đồng biến trên khoảng (0;43) và nghịch biến trên khoảng (−∞;0) và (43;+∞).
b) Tập xác định: D=R.
Ta có: y′=4x3−4x.
Nhận xét y′=0⇔[x=0x=±1
Ta có bảng biến thiên sau:
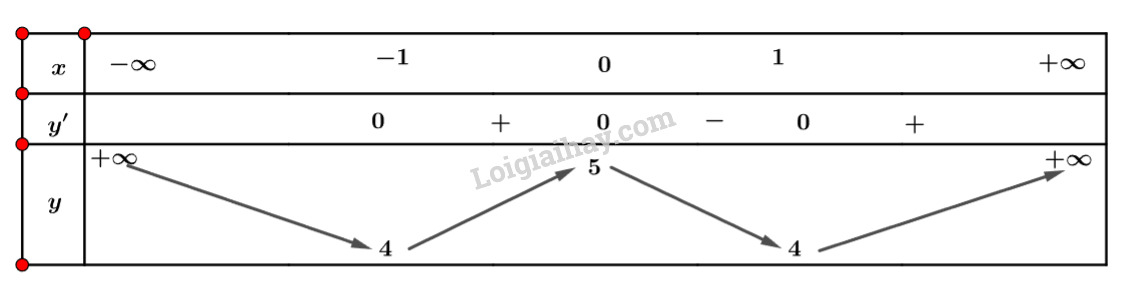
Vậy hàm số đồng biến trên khoảng (−1;0) và (1;+∞) và nghịch biến trên khoảng (−∞;−1) và (0;1).
c) Tập xác định: D=R∖{2}.
Ta có: y′=5(2−x)2.
Nhận xét y′>0∀x∈D
Ta có bảng biến thiên sau:

Vậy hàm số đồng biến trên khoảng (−∞;2) và (2;+∞).
d) Tập xác định: D=R∖{−1}.
Ta có: y′=(2x−2)(x+1)−x2+2x(x+1)2=x2+2x−2(x+1)2.
Nhận xét y′=0⇔[x=−1+√3x=−1−√3.
Ta có bảng biến thiên sau:

Vậy hàm số đồng biến trên khoảng (−∞;−1−√3) và (−1+√3;+∞) và nghịch biến trên khoảng (−1−√3;−1) và (−1;−1+√3).
Bài 4 trang 13 SGK Toán 12 Tập 1: Tìm cực trị của mỗi hàm số sau:
Lời giải:
a) Tập xác định: D=R.
Ta có: y′=6x2+6x−36.
Nhận xét y′=0⇔[x=2x=−3.
Ta có bảng biến thiên sau:
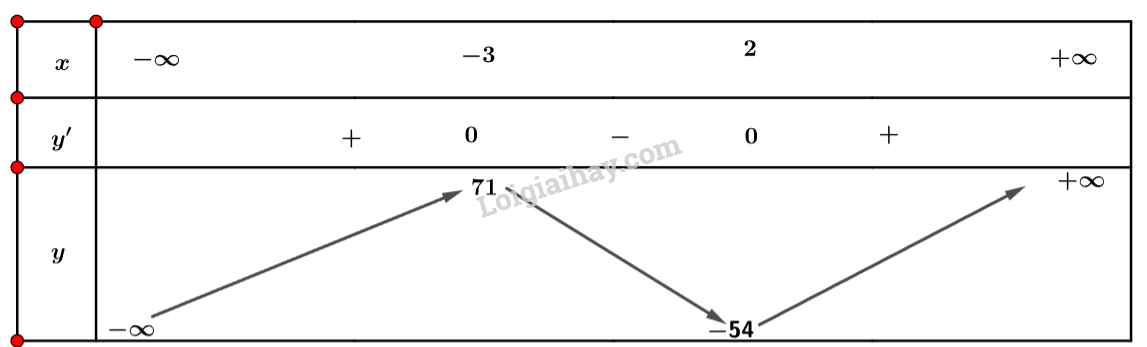
Vậy hàm số đạt cực đại tại điểm x=−3 và đạt cực tiểu tại x=2.
b) Tập xác định: D=R.
Ta có: y′=x3+4x.
Nhận xét y′=0⇔x=0.
Ta có bảng biến thiên sau:
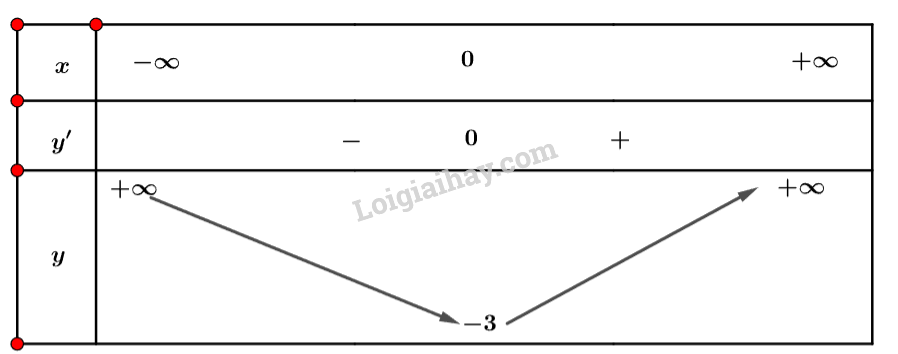
Vậy hàm số đạt cực tiểu tại x=0
c) Tập xác định: D=R∖{0}.
Ta có: y′=1+1x2.
Nhận xét y′>0∀x∈D.
Ta có bảng biến thiên sau:

Vậy hàm số không có điểm tiểu và điểm cực đại.
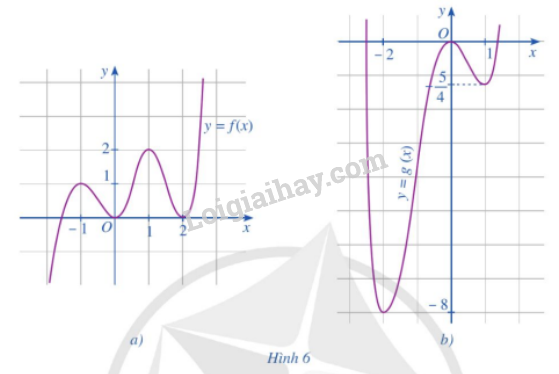
Lời giải:
a) Hàm số đồng biến trên khoảng (−∞;−1),(0;1),(2;+∞) và nghịch biến trên khoảng (−1;0),(1;2).
Hàm số đạt cực đại tại x=−1 và x=1. Hàm số đạt cực tiểu tại x=0 và x=2.
b) Hàm số đồng biến trên khoảng (−2;0),(1;+∞) và nghịch biến trên khoảng (−∞;−2),(0;1).
Hàm số đạt cực đại tại x=0. Hàm số đạt cực tiểu tại và
.
Hỏi thể tích ,
giảm trong khoảng nhiệt độ nào?
Lời giải:
Tập xác định: .
Ta có: .
Nhận xét .
Ta có bảng biến thiên sau:
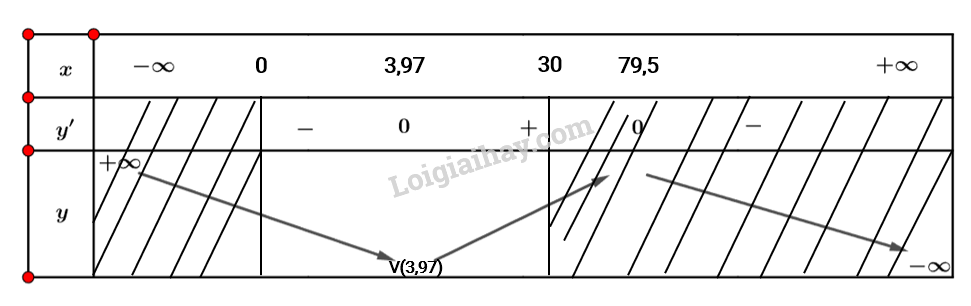
Vậy thể tích giảm trong khoảng nhiệt độ từ .
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Lời giải:
Tập xác định: .
Ta có: .
Nhận xét .

Vậy gia tốc tàu con thoi tăng trong khoảng s đầu tiên.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.