Hoạt động 1 trang 5 Toán 12 Tập 1 | Cánh diều Giải Toán lớp 12

Hoạt động 1 trang 5 Toán 12 Tập 1 | Cánh diều Giải Toán lớp 12

Mai Hương Ngày: 15-03-2024 Lớp 12

192

Với giải Hoạt động 1 trang 5 Toán 12 Tập 1 Cánh diều chi tiết trong Bài 1: Tính đơn điệu của hàm số giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Hoạt động 1 trang 5 Toán 12 Tập 1 | Cánh diều Giải Toán lớp 12

Hoạt động 1 trang 5 SGK Toán 12 Tập 1: a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập $K \subset R$ , trong đó K là một khoảng, đoạn hoặc nửa khoảng.

b) Cho hàm số $y = f (x) = x^{2}$ có đồ thị như Hình 2.

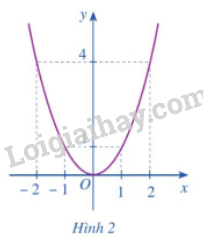
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.

- Xét dấu đạo hàm $f^{'} (x) = 2 x$ .

- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số $f (x) = x^{2}$ và dấu của đạo hàm $f^{'} (x) = 2 x$ trên mỗi khoảng $(- \infty; 0), (0; + \infty)$ .

- Hoàn thành bảng biến thiên sau:

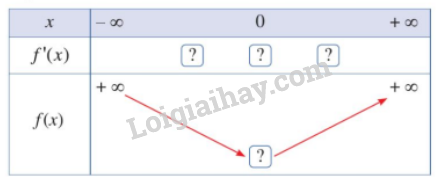
Lời giải:

a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và $f (x)$ là hàm số xác định trên K.

- Hàm số $f (x)$ được gọi là hàm số đồng biến trên K nếu với mọi $x_{1}, x_{2}$ thuộc K và $x_{1} < x_{2}$ thì $f (x_{1}) < f (x_{2})$ .

- Hàm số $f (x)$ được gọi là hàm số đồng biến trên K nếu với mọi $x_{1}, x_{2}$ thuộc K và $x_{1} < x_{2}$ thì $f (x_{1}) > f (x_{2})$ .

- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.

b)

- Hàm số đồng biến trên khoảng $(0; + \infty)$ và nghịch biến trên khoảng $(- \infty; 0)$ .

- Đạo hàm $f^{'} (x) = 2 x$ âm khi $x < 0$ và dương khi $x > 0$ .

- Hàm số $y = f (x) = x^{2}$ nghịch biến khi $f^{'} (x) = 2 x$ mang dấu âm và đồng biến khi $f^{'} (x) = 2 x$ mang dấu dương.

- Ta có bàng biến thiên sau:

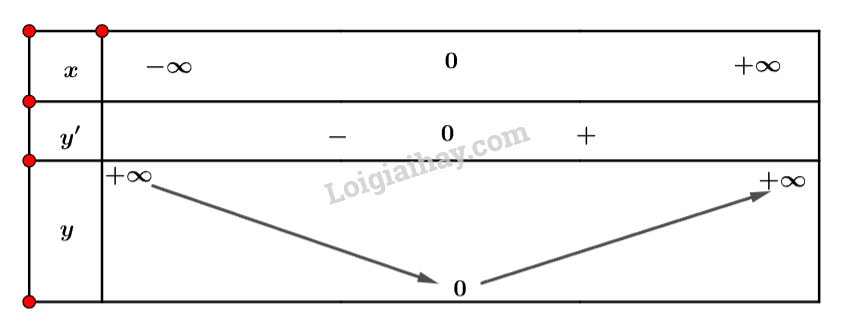
Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Hoạt động 1 trang 5 SGK Toán 12 Tập 1: a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập $K \subset R$ , trong đó K là một khoảng, đoạn hoặc nửa khoảng.

Luyện tập 1 trang 6 SGK Toán 12 Tập 1: Xét dấu $y^{'}$ rồi tìm khoảng đồng biến, nghịch biến của hàm số $y = \frac{4}{3} x^{3} - 2 x^{2} + x - 1$ .

Luyện tập 2 trang 7 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số $y = x^{4} + 2 x^{2} - 3$ .

Hoạt động 2 trang 7 SGK Toán 12 Tập 1: a) Xác định tính đồng biến, nghịch biến của hàm số $f (x) = x^{3}$ .

Luyện tập 3 trang 7 SGK Toán 12 Tập 1: Chứng minh rằng hàm số $y = \sqrt{x^{2} + 1}$ nghịch biến trên nửa khoảng $(- \infty; 0]$ và đồng biến trên nửa khoảng $[0; + \infty)$ .

Luyện tập 4 trang 8 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số sau $y = \frac{2 x - 1}{x + 2}$ .

Hoạt động 3 trang 9 SGK Toán 12 Tập 1: Dựa vào đồ thị hàm số $y = f (x) = - x^{3} - 3 x^{2} + 3$ ở Hình 3, hãy so sánh:

Hoạt động 4 trang 10 SGK Toán 12 Tập 1: Quan sát bảng biến thiên dưới đây và cho biết: a) $x_{o}$ có là điểm cực đại của hàm số $f (x)$ hay không.

Luyện tập 5 trang 11 SGK Toán 12 Tập 1: Tìm điểm cực trị của mỗi hàm số sau: a) $y = x^{4} - 6 x^{2} + 8 x + 1$ .

Bài 1 trang 13 SGK Toán 12 Tập 1: Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Bài 2 trang 13 SGK Toán 12 Tập 1: Cho hàm số $y = f (x)$ có bảng biến thiên như sau: Giá trị cực tiểu của hàm số đã cho bằng:

Bài 3 trang 13 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số sau: a) $y = - x^{3} + 2 x^{2} - 3$ b) $y = x^{4} - 2 x^{2} + 5$

Bài 4 trang 13 SGK Toán 12 Tập 1: Tìm cực trị của mỗi hàm số sau: a) $y = 2 x^{3} + 3 x^{2} - 36 x - 10$

Bài 5 trang 14 SGK Toán 12 Tập 1: Cho hai hàm số $y = f (x), y = g (x)$ có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.

Bài 6 trang 14 SGK Toán 12 Tập 1:Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T

(0^{o} C \leq T \leq 30^{o} C)

được tính bởi công thức sau:

Bài 7 trang 14 SGK Toán 12 Tập 1: Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm $t = 0 (s)$

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 12

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

299

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

325

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

348

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

296

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.