Toán 12 (Cánh diều) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Mai Hương Ngày: 15-03-2024 Lớp 12

380

Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Cánh diều) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 2 từ đó học tốt môn Toán 12.

Nội dung bài viết

Hoạt động 1 trang 15 SGK Toán 12 Tập 1:
Luyện tập 1 trang 16 SGK Toán 12 Tập 1:
Hoạt động 2 trang 16 SGK Toán 12 Tập 1:
Luyện tập 2 trang 16 SGK Toán 12 Tập 1:
Hoạt động 3 trang 17 SGK Toán 12 Tập 1:
Luyện tập 3 trang 18 SGK Toán 12 Tập 1:

Toán 12 (Cánh diều) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

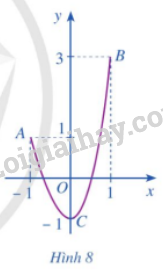
Hoạt động 1 trang 15 SGK Toán 12 Tập 1: Cho hàm số $y = f (x)$ liên tục trên đoạn $[- 1; 1]$ và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:

a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất

b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất

Lời giải:

a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất

b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất

Luyện tập 1 trang 16 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $f (x) = \sqrt{9 - x^{2}}$ trên đoạn $[- 3; 3]$ .

Lời giải:

Ta có: $x \in [- 3; 3] \Rightarrow 0 \leq x^{2} \leq 9 \Rightarrow 0 \leq 9 - x^{2} \leq 9 \Rightarrow 0 \leq \sqrt{9 - x^{2}} \leq 3$ .

Vậy ${\begin{cases} max_{[- 3; 3]} f (x) = 3 \Leftrightarrow x = 0 \\ min_{[- 3; 3]} f (x) = 0 \Leftrightarrow x = \pm 3 \end{cases}$

Hoạt động 2 trang 16 SGK Toán 12 Tập 1: Cho hàm số $f (x) = x + \frac{1}{x - 1}$ với $x > 1$ .

a) Tính $lim_{x \to 1^{+}} f (x), lim_{x \to + \infty} f (x)$ .

b) Lập bảng biến thiên của hàm số $f (x)$ trên khoảng $(1; + \infty)$ .

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $f (x)$ trên khoảng $(1; + \infty)$ .

Lời giải:

a) Ta có: ${\begin{cases} lim_{x \to 1^{+}} f (x) = + \infty \\ lim_{x \to + \infty} f (x) = + \infty \end{cases}$

b) Bảng biến thiên của hàm số trên khoảng $(1; + \infty)$ là:

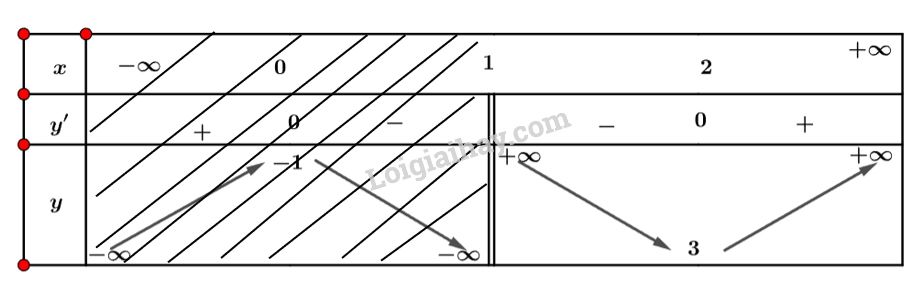
c) Hàm số có giá trị nhỏ nhất bằng 3 khi $x = 2$ và không có giá trị lớn nhất.

Luyện tập 2 trang 16 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y = \frac{2 x - 5}{x - 1}$ trên nửa khoảng $(1; 3]$ .

Lời giải:

Ta có: $y^{'} = \frac{3}{{(x - 1)}^{2}}$ .

Nhận xét $y^{'} > 0 \forall x \in D$ .

Ta có bảng biến thiên:

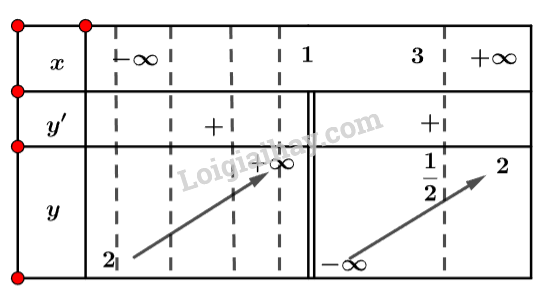
Vậy hàm số có giá trị lớn nhất bằng $\frac{1}{2}$ khi $x = 3$ và không có giá trị nhỏ nhất.

Hoạt động 3 trang 17 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = 2 x^{3} - 6 x, x \in [- 2; 2]$ có đồ thị là đường cong ở Hình 9.

a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị $M = max_{[- 2; 2]} f (x); m = min_{[- 2; 2]} f (x)$ bằng bao nhiêu.

b) Giải phương trình $f^{'} (x) = 0$ với $x \in (- 2; 2)$

c) Tính các giá trị của hàm số $f (x)$ tại hai đầu mút $- 2; 2$ và tại các điểm $x \in (- 2; 2)$ mà ở đó $f^{'} (x) = 0$

d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Lời giải:

a) Ta có: ${\begin{cases} max_{[- 2; 2]} f (x) = 4 \\ min_{[- 2; 2]} f (x) = - 4 \end{cases}$ .

b) Ta có: $f^{'} (x) = 6 x^{2} - 6$ .

Xét $f^{'} (x) = 0 \Leftrightarrow x = \pm 1$ .

c) Ta có: ${\begin{cases} f (2) = f (- 1) = 4 \\ f (- 2) = f (1) = - 4 \end{cases}$ .

d) Nhận xét: ${\begin{cases} max_{[- 2; 2]} f (x) = f (2) = f (- 1) \\ min_{[- 2; 2]} f (x) = f (- 2) = f (1) \end{cases}$ .

Luyện tập 3 trang 18 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = \sin 2 x - 2 x$ trên đoạn $[\frac{π}{2}; \frac{3 π}{2}]$ .

Lời giải:

Ta có: $f^{'} (x) = 2 \cos 2 x - 2$ .

Xét $f^{'} (x) = 0 \Leftrightarrow x = π$ .

Ta có $f (\frac{π}{2}) = - π, f (π) = - 2 π, f (\frac{3 π}{2}) = - 3 π$

Vậy hàm số $f (x) = \sin 2 x - 2 x$ có giá trị nhỏ nhất bằng $- 3 π$ khi $x = \frac{3 π}{2}$ và có giá trị lớn nhất bằng $- π$ khi $x = \frac{π}{2}$ .

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác: