Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Ôn tập chương 3 (Lý thuyết + 40 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Ôn tập chương 3 (Lý thuyết + 40 bài tập có lời giải)

I. Lý thuyết Ôn tập chương 3

Phương pháp quy nạp toán học

1. Để chứng minh một mệnh đề là đúng với mọi n ∈ ℕ* bằng phương pháp quy nạp toán học, ta tiến hành hai bước:

        ♦ Bước 1: Kiểm tra rằng mệnh đề đúng với n = 1.

        ♦ Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k (k ≥ 1) (ta gọi là giả thiết quy nạp) và chứng minh rằng nó cũng đúng với n=k+1.

2. Trong trường hợp phải chứng minh một mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là số tự nhiên) thì:

        ♦ Ở bước 1, ta kiểm tra mệnh đề đúng với n = p.

        ♦ Ở bước 2, ta giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k (k ≥ p) và chứng minh rằng nó cũng đúng với n = k + 1.

3. Phép thử với một số hữu hạn số tự nhiên, tuy không phải là chứng minh, nhưng cho phép ta dự đoán được kết quả. Kết quả này chỉ là giả thiết, và để chứng minh ta có thể dùng phương pháp quy nạp toán học.

 Dãy số

I.1 Định nghĩa

1. Định nghĩa dãy số

Mỗi hàm số u xác định trên tập các số nguyên dương N^* được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:

    u: N^* → R

    n → u(n).

Người ta thường viết dãy số dưới dạng khai triển

    u₁, u₂, u₃,…, u_n,…,

trong đó u_n = u(n) hoặc viết tắt là (u_n), và gọi u₁ là số hạng đầu, u_n là số hạng thứ n và là số hạng tổng quát của dãy số.

2. Định nghĩa dãy số hữu hạn

Mỗi hàm số u xác định trên tập M = {1,2,3,…,m} với m ∈ N^* được gọi là một dãy số hữu hạn.

Dạng khai triển của nó là u₁, u₂, u₃,…, u_n, trong đó u₁ là số hạng đầu, u_n là số hạng cuối.

I.2 Cách cho một dãy số

1. Dãy số cho bằng công thức của số hạng tổng quát

2. Dãy số cho bằng phương pháp mô tả

3. Dãy số cho bằng phương pháp truy hồi

Cách cho một dãy số bằng phương pháp truy hồi, tức là:

a) Cho số hạng đầu (hay vài số hạng đầu).

b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.

I.3 Dãy số tăng, dãy số giảm và dãy số bị chặn

1. Dãy số tăng, dãy số giảm

Định nghĩa 1

Dãy số (u_n) được gọi là dãy số tăng nếu ta có u_n+1 > u_n với mọi n ∈ N^*.

Dãy số (u_n) được gọi là dãy số giảm nếu ta có u_n+1 < u_n với mọi n ∈ N^*.

Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số (u_n) với u_n = (–3)ⁿ tức là dãy –3; 9; –27; 81,… không tăng cũng không giảm.

2. Dãy số bị chặn

Định nghĩa 2

Dãy số (u_n) được gọi là bị chặn trên nếu tồn tại một số M sao cho

    u_n ≤ M, ∀ n ∈ N^*

Dãy số (u_n) được gọi là bị chặn dưới nếu tồn tại một số m sao cho

    u_n ≥ m, ∀ n ∈ N^*

Dãy số (u_n) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho

    m ≤ u_n ≤ M, ∀ n ∈ N^*

Cấp số cộng

I.1 Định nghĩa

Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.

Số d được gọi là công sai của cấp số cộng.

Nếu (u_n) là cấp số cộng với công sai d, ta có công thức truy hồi

   u_n+1 = u_n + d với n ∈ N^*

Đặc biệt khi d = 0 thì cấp số cộng là một dãy số không đỗi (tất cả các số hạng đều bằng nhau).

I.2 Số hạng tổng quát

Định lí 1

Nếu cấp số cộng (u_n) có số hạng đầu u₁ và công sai d thì số hạng tổng quát u_n được xác định bởi công thức:

    u_n = u₁ + (n – 1 )d với n ≥ 2

I.3 Tính chất các số hạng của cấp số cộng

Định lí 2

Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là

I.4 Tổng n số hạng đầu của cấp số cộng

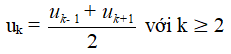
Định lí 3

Cho cấp số cộng (u_n). Đặt S_n = u₁ + u₂ + u₃ +…+ u_n. Khi đó

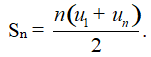
Chú ý: Vì u_n = u₁ + (n – 1)d nên công thức trên có thể viết lại là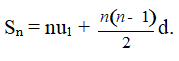 

Cấp số nhân

I.1 Định nghĩa

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

    u_n+1 = u_nq với n ∈ N^*

Đặc biệt:

    + Khi q = 0, cấp số nhân có dạng u₁, 0, 0,…, 0,…

    + Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁,…, u₁,…

    + Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0,…, 0…

I.2 Số hạng tổng quát

Định lí 1

Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức

    u_n = u₁.q^n-1 với n ≥ 2

I.3 Tính chất các số hạng của cấp số nhân

Định lí 2

Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là

    u_k² = u_k-1.u_k+1 với k ≥ 2

I.4 Tổng n số hạng đầu tiên của một cấp số nhân

Định lí 3

Cho cấp số nhân (u_n) với công bội q ≠ 1. Đặt S_n = u₁ + u₂ + … + u_n. Khi đó

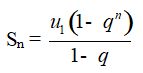
Chú ý: Nếu q = 1 thì cấp số nhân là u₁, u₁, u₁,…, u₁,… khi đó S_n = nu₁.

II. Bài tập Ôn tập chương 3

Câu 1: Cho cấp số nhân có 5 số hạng đầu là 1;4;16;64;256. Khi đó tổng của  số hạng đầu của cấp số nhân đó bằng

A.  $4^{n-1}.$

B. $\frac{n}{2}\left(1+4^{n-1}\right).$

C.   $\frac{4^n-1}{4-1}.$

D. $4.\frac{4^n-1}{4-1}.$

Đáp án: C

Câu 2: Cho cấp số nhân $\left(u_n\right)$ thỏa mãn $\left\{\begin{array}{l}{u}_2+u_4=10\\ u_1+u_3+u_5=-21\end{array}\right..$Tìm số hạng đầu và công bội

A. $\left\{\begin{array}{l}{u}_1=-16\\ q=-2\end{array}\right.$ hoặc $\left\{\begin{array}{l}{u}_1=-1\\ q=-\frac{1}{2}\end{array}\right..$

B. $\left\{\begin{array}{l}{u}_1=-16\\ q=-\frac{1}{2}\end{array}\right.$ hoặc  $\left\{\begin{array}{l}{u}_1=-1\\ q=-2\end{array}\right..$

C. $\left\{\begin{array}{l}{u}_1=16\\ q=-\frac{1}{2}\end{array}\right.$ hoặc $\left\{\begin{array}{l}{u}_1=1\\ q=-2\end{array}\right..$

D. $\left\{\begin{array}{l}{u}_1=16\\ q=-2\end{array}\right.$ hoặc $\left\{\begin{array}{l}{u}_1=1\\ q=-\frac{1}{2}\end{array}\right..$

Đáp án: B

Câu 3: Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất bằng $\frac{1}{9}$ số đo của góc nhỏ thứ ba. Số đo của các góc trong tứ giác đó lần lượt là

A. $5°; 15°; 45°; 225°.$

B.  $9°; 27°; 81°; 243°.$

C.  $7°; 21°; 63°; 269°.$

D.  $8°; 32°; 72°; 248°.$

Đáp án: B

Câu 4: Cho dãy số $\left(u_n\right)$ xác định bởi $\left\{\begin{array}{l}{u}_1=3\\ u_{n+1}=2{u_n}^2-15\end{array}\right.\left(\forall n\ge 1\right)$. Khẳng định nào sau đây đúng?

A. $\left(u_n\right)$ là cấp số cộng và không là cấp số nhân.

B. $\left(u_n\right)$ là cấp số nhân và không là cấp số cộng.

C. $\left(u_n\right)$ vừa là cấp số cộng, vừa là cấp số nhân.

D. $\left(u_n\right)$ không là cấp số cộng, không là cấp số nhân.

Đáp án: C

Câu 5: Cho cấp số cộng có tổng n số hạng đầu là $S_n=3n^2+4n,n\in {\mathbb{N}}^{\ast }$. Giá trị của số hạng thứ 10 của cấp số cộng là

A. $u_{10}=55.$

B.  $u_{10}=67.$

C.  $u_{10}=61.$

D. $u_{10}=59.$

Đáp án: C

Câu 6: Cho ba số $x; 5; 2y$ lập thành cấp số cộng và ba số $x; 4; 2y$ lập thành cấp số nhân thì $\left|x-2y\right|$ bằng

A. $\left|x-2y\right|=8.$

B. $\left|x-2y\right|=9.$

C. $\left|x-2y\right|=6.$

D. $\left|x-2y\right|=10.$

Đáp án: C

Câu 7: Cho ba số $x, 5, 3y$ theo thứ tự lập thành cấp số cộng và ba số $x, 3, 3y$ theo thứ tự lập thành cấp số nhân thì $\left|3y-x\right|$ bằng?

A. 8.

B. 6.

C. 9.

D. 10.

Đáp án: A

Câu 8: Cho cấp số nhân $\left(a_n\right)$. Dãy số nào dưới đây không phải là cấp số nhân?

A.  $a_1,a_3,a_5,\mathrm{...},a_{2n+1},\mathrm{...}$ 

B.  $a_1-3,a_2-3,a_3-3,\mathrm{...},a_n-3,\mathrm{...}$

C.   $2a_1,2a_2,2a_3,\mathrm{...2}{a}_n,\mathrm{...}$

D.  $\sqrt[3]{a_1},\sqrt[3]{a_2},\sqrt[3]{a_3},\mathrm{...},\sqrt[3]{a_n},\mathrm{...}$

Đáp án: B

Câu 9: Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình $x^4-\left(m+1\right)x^2+m=0$ có 4 nghiệm phân biệt lập thành cấp số cộng. Tổng giá trị của các phần tử thuộc S là

A. $\frac{91}{9}.$

B. $\frac{28}{9}.$

C. $\frac{13}{9}.$

D. $\frac{82}{9}.$

Đáp án: D

Câu 10: Cho dãy số $\left(u_n\right)$ xác định bởi $\left\{\begin{array}{l}{u}_1=3\\ u_{n+1}=6u_n+15\left(\forall n\ge 1\right)\end{array}\right.$. Tìm chữ số hàng đơn vị của $u_{2018}?$

A. 6.

B. 9.

C. 4.

D. 3.

Đáp án: D

Câu 11: Một hãng taxi áp dụng mức giá đối với khách hàng theo hình thức bậc thang như sau: Mỗi bậc áp dụng cho 10 km. Bậc 1 (áp dụng cho 10km đầu) có giá trị 10.000đ/1km, giá mỗi km ở các bậc tiếp theo giảm 5% so với giá của bậc trước đó. Bạn An thuê hãng taxi đó để đi quãng đường 114km, nhưng khi đi được 50km thì bạn Bình đi chung hết quãng đường còn lại. Tính số tiền mà bạn An phải trả, biết rằng mức giá áp dụng từ lúc xe xuất phát và số tiền trên quãng đường đi chung bạn An chỉ phải trả 20% (Kết quả làm trong đến hàng nghìn).

A. 885000.

B. 433000.

C. 539000.

D. 559000.

Đáp án: C

Câu 12: Dãy số nào sau đây là một cấp số nhân?

A. $2,4,6,8,\mathrm{....}$

B. $2,4,8,16,\mathrm{...}$

C.  $1,2,3,4,\mathrm{...}$

D. $1,3,5,7,\mathrm{....}$

Đáp án: B

Câu 13: Dãy số $\left(u_n\right)$ cho bởi: $\left\{\begin{array}{l}{u}_1=2\\ u_{n+1}=2u_n-3\end{array}\right.,\forall n\ge 1.$Số hạng thứ 3 của dãy là

A.  $u_3=-6.$

B.  $u_3=3.$

C.  $u_3=1.$

D.  $u_3=-1.$

Đáp án: D

Câu 14: Cho dãy số $\left(u_n\right)$ với $u_n=\frac{3^n}{n^3}$ số hạng thứ hai của dãy là?

A. 1.

B. $\frac{3}{4}.$

C. $\frac{3}{2}.$

D. $\frac{9}{8}.$

Đáp án: D

Câu 15: Cho dãy số $u_n={\left(-2\right)}^n$. Khẳng định nào sau đây là đúng?

A. Dãy bị chặn.

B. Dãy không bị chặn.

C. Dãy giảm.

D. Dãy tăng.

Đáp án: B

Câu 16: Cho cấp số nhân $\left(u_n\right)$ có $u_1=2,q=3.$ Khi đó số hạng thứ 3 của cấp số nhân là

A. 12.

B. 8.

C. 54.

D. 18.

Đáp án: D

Câu 17: Cho cấp số cộng $\left(u_n\right)$, biết $u_1=3$ và $u_6=13$. Tính công sai của cấp số cộng đã cho.

A. d = 10

B. d = 2

C. $d=\sqrt[5]{\frac{13}{3}}$

D. d= $\frac{5}{3}$

Đáp án: B

Câu 18: Cho cấp số nhân lùi vô hạn $\left(u_n\right)$ có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây

A.  $S=\frac{1}{1-q}.$

B.  $S=\frac{u_1}{1-q}.$

C.  $S=\frac{u_1}{1+q^n}.$

D.  $S=\frac{u_1}{1-q^n}.$

Đáp án: B

Câu 19: Cho dãy số $\left(u_n\right)$với $\left\{\begin{array}{l}{u}_1=\frac{1}{2}\\ u_n=\frac{1}{2-u_{n-1}}\end{array}\right.$với $n\ge 2$. Giá trị của $u_4$bằng

A. $\frac{3}{4}.$

B.  $\frac{4}{5}.$

C.  $\frac{5}{6}.$

D.  $\frac{6}{7}.$

Đáp án: B

Câu 20: Cho dãy số $\left\{\begin{array}{l}{u}_1=1\\ u_n=2u_{n-1}+3u_{n-2}\left(n\in {\mathbb{N}}^{\ast }\right)\end{array}\right..$ Khi đó số hạng thứ n+3 là

A. $u_{n+3}=2u_{n+2}+3u_{n+1}.$

B.  $u_{n+3}=2u_{n+2}+3u_n.$

C.  $u_{n+3}=2u_{n-2}+3u_{n+1}.$

D.  $u_{n+3}=2u_{n+2}+3u_{n-1}.$

Đáp án: A

Câu 21: Cho dãy số có công thức tổng quát là $u_n=2^n$ thì số hạng thứ n + 3 là?

A.  $u_{n+3}=2^3.$

B.   $u_{n+3}={8.2}^n.$

C.   $u_{n+3}={6.2}^n.$

D.   $u_{n+3}=6^n.$

Đáp án: B

Câu 22: Cho cấp số nhân $\left(u_n\right)$ có $u_5+u_{19}=90.$Tính tổng của 23 số hạng đầu tiên của cấp số cộng trên.

A. 1030.

B. 1025.

C. 1035.

D. 1040.

Đáp án: A

Câu 23: Dãy số $\left(u_n\right)$ nào bị chặn trong các dãy số sau khi biết

A. $u_n=\frac{\sqrt{n^2+3}}{2n+1}$

B. $u_n=\frac{n^2+n-1}{2n-1}$

C.  $u_n={\left(-1\right)}^n.\left(3n+2\right).$

D.  $u_n=2n-1.$

Đáp án: A

Câu 24: Tìm số thực a để dãy số $\left(u_n\right)$ với $u_n=\frac{a{n}^2+1}{2n^2+3}$ là dãy số giảm?

A. $a>\frac{2}{3}.$

B.  $a<\frac{3}{2}.$

C.  $a>\frac{3}{2}.$

D.  $a<\frac{2}{3}.$

Đáp án: D

Câu 25: Tìm số hạng đầu $u_1$ và công sai d của cấp số cộng $\left(u_n\right)$ biết $u_2=7;u_3=4.$

A.  $u_1=4;d=-3.$

B.  $u_1=10;d=-3.$

C.  $u_1=1;d=-3.$

D. $u_1=1;d=3.$

Đáp án: B

Câu 26: Xét dãy các số tự nhiên chẵn liên tiếp $\left(u_n\right):0;2;4;6;8;\mathrm{....}$Số 2018 là số hạng thứ mấy?

A. 2016.

B. 2018.

C. 1010.

D. 1009.

Đáp án: C

Câu 27: Một khu rừng có trữ lượng gỗ là ${4.10}^5$ mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?

A. ${4.10}^5.{\left(0,05\right)}^5.$

B. $4.{\left(10,4\right)}^5.$

C. ${4.10}^5.{\left(1,04\right)}^4.$

D. ${4.10}^5.{\left(1,4\right)}^5.$

Đáp án: C

Câu 28: Tổng $1+2+2^2+\mathrm{...}+2^{2017}$ có giá trị bằng

A. $2^{2018}.$

B. $2^{2017}.$

C. $2^{2018}-1.$

D. $2^{2017}-1.$

Đáp án: C

Câu 29: Tổng $1+2+2^2+\mathrm{...}+2^{2017}$ có giá trị bằng

A.  $2^{2017}-1.$

B.   $2^{2017}.$

C.   $2^{2018}-1.$

D.   $2^{2018}.$

Đáp án: C

Câu 30: Cho cấp số cộng $\left(u_n\right)$ có $u_1=123$ và $u_3-u_{15}=84.$ Số hạng $u_{17}$ là

A. 4.

B. 242.

C. 11.

D. 235.

Đáp án: C

Câu 31: Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên

A. -3 hoặc – 6

B. – 4 hoặc -2

C. -1 hoặc -5

D. -4 hoặc - 7

Đáp án: B

Câu 32: Tìm x để 3 số : 1 - x; x² ; x + 1 theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của x.

B. x = ± 2 .

C. x = ± 1 .

D. x = 0

Đáp án: B

Câu 33: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25°. Tìm 2 góc còn lại?

A. 65° ; 90°.

B. 75° ; 80°.

C. 60° ; 95°.

D. 55°; 100°.

Đáp án: C

Câu 34: Cho cấp số nhân (u_n) với u₁ = -1; q = -1/10 . Số 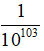 là số hạng thứ mấy của (u_n) ?

A. Số hạng thứ 103

B. Số hạng thứ 104

C. Số hạng thứ 105

D. Đáp án khác

Đáp án: B

Câu 35: Mệnh đề nào dưới đây sai?

A. Dãy số 1; -2; 4; -8; 16; -32; 64 là một cấp số nhân.

B. Dãy số 7; 0; 0; 0;... là một cấp số nhân.

C. Dãy số (u_n):u_n = n.6^{n + 1} là một cấp số nhân.

D. Dãy số (v_n):v_n = (-1)ⁿ.3²ⁿ là một cấp số nhân.

Đáp án: C

Câu 36: Dãy số (u_n) có phải là cấp số nhân không ? Nếu phải hãy xác định số công bội ? Biết rằng u_n = 4.3ⁿ

A. q = 3

B. q = 2

C. q = 4

D. q = ∅

Đáp án: A

Câu 37: Cho cấp số nhân (u_n) với u₁ = 3; q = -2 . Số 192 là số hạng thứ mấy của (u_n) ?

A. Số hạng thứ 5.

B. Số hạng thứ 6.

C. Số hạng thứ 7.

D. Không là số hạng của cấp số đã cho.

Đáp án: A

Câu 38: Cho dãy số (u_n) với 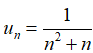.Khẳng định nào sau đây là sai?

A. Năm số hạng đầu của dãy là: ;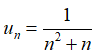

B. Là dãy số tăng.

C. Bị chặn trên bởi số M = 1/2.

D. Không bị chặn.

Đáp án: B

Câu 39: Xét tính tăng giảm của các dãy số sau: 

A. Dãy số tăng

B. Dãy số giảm

C. Dãy số không tăng không giảm

D. Cả A, B, C đều sai

Đáp án: A

Câu 40: Cho cấp số cộng (u_n) có: u₁ = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:

A. 1, 6

B. 6

C. 0,5

D. 0,6

Đáp án: C