Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Cấp số cộng (Lý thuyết + 40 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Cấp số cộng (Lý thuyết + 40 bài tập có lời giải)
I. Lý thuyết Cấp số cộng
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi
un+1 = un + d với n ∈ N*
Đặc biệt khi d = 0 thì cấp số cộng là một dãy số không đỗi (tất cả các số hạng đều bằng nhau).
Định lí 1
Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1 )d với n ≥ 2
Định lí 2
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là
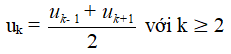
Định lí 3
Cho cấp số cộng (un). Đặt Sn = u1 + u2 + u3 +…+ un. Khi đó
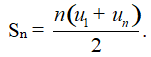
Chú ý: Vì un = u1 + (n – 1)d nên công thức trên có thể viết lại là 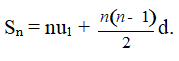
II. Bài tập Cấp số cộng
Câu 1: Khẳng định nào sau đây là sai?
A. Dãy số là một cấp số cộng:
B. Dãy số là một cấp số cộng:
C. Dãy số :là cấp số cộng
D. Dãy số: không phải là một cấp số cộng
Đáp án: B
Câu 2: Cho một cấp số cộng có . Hãy chọn kết quả đúng
A. Dạng khai triển :
B. Dạng khai triển :
C. Dạng khai triển :
D. Dạng khai triển:
Đáp án: D
Câu 3. Cho một cấp số cộng có . Tìm d ?
A. .
B. .
C. .
D. .
Đáp án: C
Câu 4: Cho một cấp số cộng có . Tìm ?
A.
B.
C.
D.
Đáp án: A
Câu 5: Cho cấp số cộng có: . Số hạng thứ 7 của cấp số cộng này là:
A. 1,6
B. 6
C. 0,5
D. 0,6
Đáp án: C
Câu 6: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng 25o. Tìm 2 góc còn lại?
A. 65o ; 90o.
B. 75o ; 80o.
C. 60o ; 95o.
D. 60o ; 90o.
Đáp án: D
Câu 7: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. .
B. .
C. .
D. .
Đáp án: B
Câu 8: Cho theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A.
B.
C.
D.
Đáp án: C
Câu 9: Cho cấp số cộng thỏa: . Tính số hạng thứ 100 của cấp số ;
A.
B.
C.
D.
Đáp án: B
Câu 10: Tam giác ABC có ba góc A,B,C theo thứ tự đó lập thành cấp số cộng và C = 5A. Xác định số đo các góc A,B,C.
A.
B.
C.
D.
Đáp án: D
Câu 11: Cho tam giác ABC biết ba góc tam giác lập thành cấp số cộng và tính các góc của tam giác
A.
B.
C.
D.
Đáp án: A
Câu 12: Cho theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?
A. .
B. .
C. .
D. .
Đáp án: B
Câu 13. Cho dãy số có:. Khẳng định nào sau đây là đúng?
A. .
B. .
C. .
D. .
Đáp án: C
Câu 14. Cho dãy số có:. Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Đáp án: A
Câu 15. Cho dãy số có d = –2; S8 = 72. Tính u1 ?
A.
B.
C.
D.
Đáp án: A
Câu 16. Cho dãy số có Tính ?
A.
B.
C.
D.
Đáp án: D
Câu 17: Cho một cấp số cộng có và tổng 100 số hạng đầu bằng 24850. Tính
A.
B.
C.
D.
Đáp án: A
Câu 18: Xác định x để 3 số: theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x.
B. .
C.
D.
Đáp án: C
Câu 19: Xác định để 3 số : theo thứ tự lập thành một cấp số cộng?
A.
B.
C.
D. Không có giá trị nào của x.
Đáp án: B
Câu 20: Xác định m để phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
A.
B.
C.
D.
Đáp án: B
Câu 21: Xác định m để phương trình (1) có bốn nghiệm phân biệt lập thành cấp số cộng.
A. hoặc
B. hoặc
C. hoặc
D. hoặc
Đáp án: B
Câu 22: Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này
A. 105
B. 27
C. 108
D. 111
Đáp án: C
Câu 23: Cho một cấp số cộng có u1 = -3; u6 = 27. Tìm d ?
A. d = 5
B. d = 7
C. d = 6
D. d = 8
Đáp án: C
Câu 24: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
Đáp án: D
Câu 25: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
A. 1,6
B. 6
C. 0,5
D. 0,6
Câu 26: Cho cấp số cộng (un) thỏa: 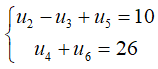 . Xác định công thức tổng quát của cấp số
. Xác định công thức tổng quát của cấp số
A. un = 3n - 2
B. un = 3n - 4
C. un = 3n - 3
D. un = 3n - 1
Đáp án: A
Câu 27: Cho hai cấp số cộng (un): 4, 7, 10, 13, 16, ...và (vn):1, 6, 11, 16, 21, ...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?
A.10
B. 20
C. 30
D. 40
Câu 28: Cho cấp số cộng (un) thỏa mãn: 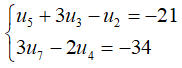 . Tính số hạng thứ 100 của cấp số ;
. Tính số hạng thứ 100 của cấp số ;
A. - 243
B. - 295
C. - 231
D. - 294
Đáp án: B
Câu 29: Cho cấp số cộng (un) thỏa mãn: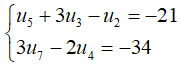 .Tính tổng 15 số hạng đầu của cấp số ;
.Tính tổng 15 số hạng đầu của cấp số ;
A. - 244
B. - 274
C. - 253
D. - 285
Đáp án: D
Câu 30: Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên
A. -3 hoặc – 6
B. – 4 hoặc -2
C. -1 hoặc -5
D. -4 hoặc - 7
Câu 31: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25°. Tìm 2 góc còn lại?
A. 65° ; 90°.
B. 75° ; 80°.
C. 60° ; 95°.
D. 55°; 100°.
Câu 32: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. a2 + c2 = 2ab + 2bc.
B. a2 - c2 = 2ab - 2bc.
C. a2 + c2 = 2ab - 2bc.
D. a2 - c2 = ab - bc.
Câu 33: Tìm x để 3 số : 1 - x; x2 ; x + 1 theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x.
B. x = ± 2 .
C. x = ± 1 .
D. x = 0
Câu 34: Cho các dãy số (un) sau :

Hỏi có bao nhiêu dãy số là cấp số cộng ?
A. 1
B. 2
C.3
D.4
Câu 35: Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng. Tính tổng của ba số viết xen giữa đó ?
A. 36.
B. 30.
C.39.
D. 34
Câu 36: Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc A bằng 30°. Tìm công sai d ?
A. 40
B. 30
C. 35
D. 45
Câu 37: Cho cấp số cộng (un) thỏa mãn 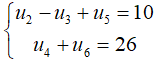 . Xác định công sai?
. Xác định công sai?
A. d = 3
B. d = 5
C. d = 6
D. d = 4
Câu 38: Cho dãy số (un) có d = –2; S8 = 72. Tính u1 ?
A. u1 = -8
B. u1 = 16
C. u1 = 4
D. u1 = 8
Câu 39: Cho dãy số (un) có u1 = -1; d = 2; Sn = 483 Tính số các số hạng của cấp số cộng?
A. n = 20
B. n = 21
C. n = 22
D. n = 23
Câu 40: Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?
A. 6
B. 7
C. 5
D. 8
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.