Tính từ số hạng của CSC và kết luận.

Sử dụng công thức $u_{n+1}=u_n+d$.

Lời giải:

Ta có:

$u_6=u_5+d=u_5+3$ $=\frac{35}{3}+3=\frac{44}{3}$

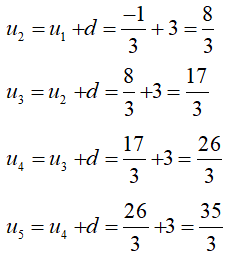
Dạng khai triển của cấp số cộng đó là: ${\displaystyle \frac{-1}{3};\frac{8}{3};\frac{17}{3};\frac{26}{3};\frac{35}{3};\frac{44}{3}}$.

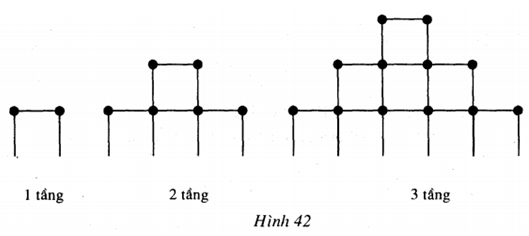
Hỏi: Nếu tháp có 100 tầng thì cần bao nhiêu que diêm để xếp tầng đế của tháp?

Lời giải:

Xây 1 tầng cần 2 que diêm để xếp tầng đế

Xây 2 tầng cần 4 que diêm để xếp tầng đế (4 = 2 + 1.2)

Xây 3 tầng cần 6 que diêm để xếp tầng đế ( 6 = 2 + 2.2)

Xây 100 tầng cần 200 que diêm để xếp tầng đế (200 = 2 + 99.2).

b) Tính tổng các số hạng của cấp số cộng.

Lời giải:

a)

Tổng các số hạng từng cột bằng nhau và bằng 26.

b)

Tổng các số hạng của cấp số cộng là: ${\displaystyle \frac{26.8}{2}}=104$.

Bài tập trang 97, 98 SGK Toán 11

a) $u_n=5-2n$;

b) $u_n={\displaystyle \frac{n}{2}}-1$;

c) $u_n=3^n$;

d) $u_n={\displaystyle \frac{7-3n}{2}}$.

Phương pháp giải:

Sử dụng định nghĩa cấp số cộng:

Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn) trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.

Ta chứng minh $u_{n+1}-u_n=const$.

Lời giải:

a)

Ta có: $u_1=5-2.1=3$

Với mọi $n\in {\mathbb{N}}^{\ast }$ ta có: 

$u_{n+1}-u_n=5-2\left(n+1\right)-\left(5-2n\right)$

$=5-2n-2-5+2n=-2$

$\Rightarrow u_{n+1}=u_n-2,\mathrm{\forall }n\in N^{\ast }$

a) $\{\begin{array}{l}{u}_1-u_3+u_5=10\\ u_1+u_6=17\end{array}$

b) $\{\begin{array}{l}{u}_7-u_3=8\\ u_2.u_7=75\end{array}$

Phương pháp giải:

a) Sử dụng công thức SHTQ: $u_n=u_1+(n–1)d$.

b) Sử dụng công thức SHTQ: $u_n=u_1+(n–1)d$.

Lời giải:

a) Ta có :

$\begin{array}{l}{u}_3=u_1+2d;\\ u_5=u_1+4d;\\ u_6=u_1+5d\end{array}$

Theo đề bài ta có :

$\begin{array}{l}\{\begin{array}{l}{u}_1-u_3+u_5=10\\ u_1+u_6=17\end{array}\\ \iff \{\begin{array}{l}{u}_1-\left(u_1+2d\right)+u_1+4d=10\\ u_1+u_1+5d=17\end{array}\\ \iff \{\begin{array}{l}{u}_1+2d=10\\ 2u_1+5d=17\end{array}\iff \{\begin{array}{l}{u}_1=16\\ d=-3\end{array}\end{array}$

b) Ta có: $u_7=u_1+6d;u_3=u_1+2d;u_2=u_1+d$

Do đó theo đề bài ta có:

$\begin{array}{l}\{\begin{array}{l}{u}_7-u_3=8\\ u_2.u_7=75\end{array}\\ \iff \{\begin{array}{l}{u}_1+6d-u_1-2d=8\\ \left(u_1+d\right)\left(u_1+6d\right)=75\end{array}\\ \iff \{\begin{array}{l}4d=8\\ \left(u_1+d\right)\left(u_1+6d\right)=75\end{array}\\ \iff \{\begin{array}{l}d=2\\ \left(u_1+2\right)\left(u_1+12\right)=75\end{array}\\ \iff \{\begin{array}{l}d=2\\ u_1^2+14u_1+24=75\end{array}\\ \iff \{\begin{array}{l}d=2\\ u_1^2+14u_1-51=0\end{array}\\ \iff \{\begin{array}{l}d=2\\ [\begin{array}{l}{u}_1=3\\ u_1=-17\end{array}\end{array}\end{array}$

$\iff [\begin{array}{l}\{\begin{array}{l}d=2\\ u_1=3\end{array}\\ \{\begin{array}{l}d=2\\ u_1=-17\end{array}\end{array}$

a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?

b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

Sử dụng các công thức:

$\begin{array}{l}{u}_n=u_1+\left(n-1\right)d\\ S_n=n{u}_1+\frac{n\left(n-1\right)}{2}d\end{array}$

Lời giải:

a) Ta có:

$\begin{array}{l}{u}_n=u_1+(n-1).d\\ \Rightarrow n=\frac{u_n-u_1}{d}+1;d=\frac{u_n-u_1}{n-1}\\ S_n=n.u_1+\frac{n(n-1)}{2}.d\Rightarrow u_1=\frac{2.S_n-n(n-1).d}{2n}\\ S_n=\frac{n(u_1+u_n)}{2}\Rightarrow u_1=\frac{2.S_n-n.u_n}{n}\end{array}$

Dựa vào các công thức trên thấy cần phải biết ít nhất 3 đại lượng để tìm được các đại lượng còn lại.

b)

Dòng đầu: Biết $u_1=-2;u_{20}=55$. Tìm d và $S_{20}$.

Ta có $u_{20}=u_1+19d$

$\iff 55=-2+19d\iff d=3$

$S_{20}=\frac{20\left(u_1+u_{20}\right)}{2}$ $=\frac{20.\left(-2+55\right)}{2}=530$

Dòng 2: Biết $d=-4;S_{15}=120$, tìm $u_1$ và $u_{15}$.

Ta có $S_{15}=15u_1+\frac{15.\left(15-1\right)}{2}.d$

$\iff 120=15.u_1+105.\left(-4\right)$

$\iff 15u_1=540\iff u_1=36$

$\Rightarrow u_{15}=u_1+14d=36+14.\left(-4\right)=-20$

Dòng 3: Biết $u_1=3;d=\frac{4}{27};u_n=7$. Tìm n và tính $S_n$.

Ta có $u_n=u_1+\left(n-1\right)d$

$\iff 7=3+\left(n-1\right).\frac{4}{27}\iff n=28$

$S_{28}=28u_1+\frac{28.\left(28-1\right)}{2}.d$

$=28.3+378.\frac{4}{27}=140$

Dòng 4: Biết $u_{12}=17$ và $S_{12}=72$. Tìm $u_1$ và $d$.

$\begin{array}{l}{S}_{12}=\frac{12\left(u_1+u_{12}\right)}{2}\\ \iff 72=\frac{12\left(u_1+17\right)}{2}\\ \iff u_1+17=12\\ \iff u_1=-5\\ u_{12}=u_1+11d\\ \iff 17=-5+11d\\ \iff 22=11d\iff d=2\end{array}$

Dòng 5: Biết $u_1=2;d=-5$ và $S_n=-205$. Tìm n và tính $u_n$.

Ta có

$\begin{array}{l}{S}_n=n{u}_1+\frac{n\left(n-1\right)}{2}d\\ \iff -205=n.2+\frac{n\left(n-1\right)}{2}.\left(-5\right)\\ \iff -410=4n-5n\left(n-1\right)\\ \iff 5n^2-9n-410=0\\ \iff [\begin{array}{l}n=10\\ n=-\frac{41}{5}\left(loai\right)\end{array}\\ \Rightarrow n=10\\ \Rightarrow u_{10}=u_1+9d\\ =2+9.\left(-5\right)=-43\end{array}$

Vậy ta điền được bảng như sau :

a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Phương pháp giải:

a)

Đây là một bài toán cấp số cộng.

- Xác định số hạng thứ nhất $u_1$.

- Xác định công sai $d$.

Sử dụng công thức số hạng tổng quát: $u_n=u_1+(n-1)d$

b)

+) độ cao mặt sàn tầng hai tương ứng với bậc nào của cầu thang?

+) áp dụng câu a), tính độ cao từ bậc đó so với mặt sân.

Lời giải:

a) Đổi: $18cm=0,18m$

Gọi $u_i$ là độ cao từ bậc thứ $i$ (của cầu thang) so với mặt sân.

Vì mỗi bậc cao $0,18m,$ sàn nhà lại cao hơn mặt sân $0,5m$ nên bậc đầu tiên sẽ cao hơn so với mặt sân là:

$0,18+0,5=0,68(m)$ hay $u_1=0,68$

Từ các bậc sau thì: bậc sau cao hơn bậc ngay trước $0,18m$, nên độ cao so với mặt sân của hai bậc liên tiếp cũng hơn kém nhau $0,18m$. Hay $u_{n+1}=u_n+0,18;21\ge n\ge 1$

Do đó, độ cao từ các bậc so với mặt sân, từ bậc 1 đến bậc 21 tạo thành một CSC với $u_1=0,68$ và công sai $d=0,18$

Vậy độ cao từ bậc thứ $n$ so với mặt sân là: $u_n=0,68+(n-1).0,18=0,5+n.0,18.$

b)

Vì mặt sàn tầng hai có cùng độ cao với bậc thứ 21 (bậc cao nhất) của cầu thang.

Nên chiều cao mặt sàn tầng hai so với mặt sân cũng là độ cao từ bậc thứ 21 so với mặt sân (được kí hiệu là u_21 ở câu a)

Vậy chiều cao mặt sàn tầng hai so với mặt sân là $u_{21}=0,5+21.0,18=4,28(m)$.