Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 2: Dãy số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về dãy số lớp 11.
Giải bài tập Toán 11 Bài 2: Dãy số
Trả lời câu hỏi giữa bài:
Câu hỏi 1 trang 85 SGK Đại số và Giải tích 11: Cho hàm số , . Tính
Phương pháp giải:
Thay lần lượt từng giá trị của n vào f.
Lời giải:
Câu hỏi 2 trang 86 SGK Đại số và Giải tích 11: Hãy nêu các phương pháp cho một hàm số và ví dụ minh họa.
Lời giải:
- Hàm số cho bằng bảng
Ví dụ:
- Hàm số cho bằng công thức:
Ví dụ: .
Câu hỏi 3 trang 86 SGK Đại số và Giải tích 11: Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau:
a) Dãy nghịch đảo của các số tự nhiên lẻ;
b) Dãy các số tự nhiên chia cho dư .
Lời giải:
a)
Năm số hạng đầu:
Số hạng tổng quát của dãy số: .
b)
Năm số hạng đầu:
Số hạng tổng quát của dãy số: với .
Câu hỏi 4 trang 87 SGK Đại số và Giải tích 11: Viết mười số hạng đầu của dãy Phi-bô-na-xi.
Phương pháp giải:
Dãy Phi-bô-na-xi có hai số hạng đầu bằng 1, số hạng sau bằng tổng hai số ngay trước nó.
Lời giải:
Mười số hạng đầu của dãy Phi-bô-na-xi: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55.
Câu hỏi 5 trang 89 SGK Đại số và Giải tích 11: Cho các dãy số và và với ;
a) Tính , ;
b) Chứng minh và , với mọi .
Phương pháp giải:
a) Thay giá trị vào hai dãy tìm ,
b) Xét hiệu
Lời giải:
a) ;
b) Ta có:
⇒ ⇒ , .
⇒ ⇒ ,.
Câu hỏi 6 trang 90 SGK Đại số và Giải tích 11: Chứng minh các bất đẳng thức với mọi .
Phương pháp giải:
Xét hiệu hai vế cần đánh giá và so sánh với 0.
Lời giải:
Bài tập trang 92 SGK Toán 11
Bài 1 trang 92 SGK Đại số và Giải tích 11: Viết năm số hạng đầu của các dãy số có số hạng tổng quát un cho bởi công thức:
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
a) Muốn viết 5 số hạng đầu tiên của dãy số đã cho ta tính lần lượt tại .
b) Muốn viết 5 số hạng đầu tiên của dãy số đã cho ta tính lần lượt tại .
c) Muốn viết 5 số hạng đầu tiên của dãy số đã cho ta tính lần lượt tại .
d) Muốn viết 5 số hạng đầu tiên của dãy số đã cho ta tính lần lượt tại .
Lời giải:
a) Ta có: ; ; ; ;
Năm số hạng đầu của dãy số là:
; ,
b)
Ta có: ; ; ; ; .
Năm số hạng đầu của dãy số là
c)
Ta có: , ; ; ; .
Năm số hạng đầu của dãy số là
;
d)
Ta có: , , , , .
Năm số hạng đầu của dãy số là
.
Bài 2 trang 92 SGK Đại số và Giải tích 11: Cho dãy số , biết: với .
a) Viết năm số hạng đầu của dãy số;
b) Chứng minh bằng phương pháp quy nạp: .
Phương pháp giải:
a) Công thức đã cho có thể hiểu là số hạng sau bằng số hạng trước cộng với .
b)
Nội dung phương pháp quy nạp toán học.
Bước 1: Chứng minh đẳng thức đã cho đúng với .
Bước 2: Giả sử đẳng thức đúng đến (giả thiết quy nạp). Ta chứng minh đẳng thức đúng với .
Khi đó đẳng thức đúng với mọi .
Lời giải:
a)
.
.
.
.
.
Năm số hạng đầu của dãy số là:
b)
Chứng minh (*) bằng phương pháp quy nạp:
+) Do nên (*) đúng với
+) Giả sử (*) đúng với , tức là .
Ta cần chứng minh (*) đúng với , tức là chứng minh .
Thật vậy, từ giả thiết với mọi ta suy ra:
hay
Do đó (*) đúng với .
Kết luận: Vậy hệ thức đúng với mọi .
Bài 3 trang 92 SGK Đại số và Giải tích 11: Dãy số un cho bởi: .
a) Viết năm số hạng đầu của dãy số.
b) Dự đoán công thức số hạng tổng quát và chứng minh công thức đó bằng phương pháp quy nạp.
Phương pháp giải:
a) Để viết năm số hạng đầu tiên của dãy số ta tính lần lượt tại .
b)
Dựa vào các giá trị dự đoán công thức tổng .
Sử dụng phương pháp quy nạp toán học.
Bước 1: Chứng minh đẳng thức đã cho đúng với .
Bước 2: Giả sử đẳng thức đúng đến (giả thiết quy nạp). Chứng minh đẳng thức đúng đến .
Lời giải:
a) Ta có:
Năm số hạng đầu của dãy số là
b)
Ta có:
...........
Từ trên ta dự đoán , với (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với , rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với , tức là có với , ta cần chứng minh
Theo công thức dãy số, ta có:
.
Như vậy công thức (1) đúng với .
Vậy công thức (1) được chứng minh.
Bài 4 trang 92 SGK Đại số và Giải tích 11: Xét tính tăng, giảm của các dãy số un biết:
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
a) Để xét tính tăng, giảm có dãy số ta có 2 cách sau:
Cách 1: Xét hiệu
+) Nếu hiệu trên lớn hơn chứng tỏ do đó dãy số là dãy tăng.
+) Nếu hiệu trên nhỏ hơn chứng tỏ do đó dãy số là dãy giảm.
Cách 2: Xét thương
+) Nếu thương trên lớn hơn chứng tỏ do đó dãy số là dãy tăng.
+) Nếu thương trên nhỏ hơn chứng tỏ do đó dãy số là dãy giảm.
d) Xét thương (vì với mọi ) rồi so sánh với .
Lời giải:
a) Xét hiệu
Vậy dãy số đã cho là dãy số giảm.
Cách khác:
Với mọi ta có:
Do đó là dãy số giảm.
b)
Xét hiệu
Vậy dãy số đã cho là dãy số tăng.
Cách khác:
Với mọi n thuộc N* ta có:
Vậy dãy số đã cho là dãy số tăng.
c)
Nhận xét:
⇒ dãy số không tăng, không giảm.
Chú ý:
Các dãy số mà có số hạng đang dấu là dãy số không tăng và cũng không giảm.
d)
Ta có:
với mọi
(Vì )
Vậy dãy số đã cho là dãy số giảm dần.
Cách khác:
Bài 5 trang 92 SGK Đại số và Giải tích 11: Trong các dãy số sau, dãy số nào bị chặn dưới, dãy số nào bị chặn trên, dãy số nào bị chặn?
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Dãy số được gọi là bị chặn trên nếu tồn tại một số M sao cho.
Dãy số được gọi là bị chặn dưới nếu tồn tại một số m sao cho .
Dãy số được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho .
Lời giải:
a) Ta có:
Do đó bị chặn dưới bởi 1.
Ngoài ra, không bị chặn trên vì không tồn tại số M nào để với mọi .
b)
Dễ thấy .
Mặt khác, vì:
Suy ra với mọi .
Vậy dãy số bị chặn.
c)
Dễ thấy với mọi
Ta có:
Vậy , tức dãy số bị chặn.
d)
Ta có:
Vậy , tức là dãy số là dãy bị chặn.
Lý thuyết Bài 2: Dãy số
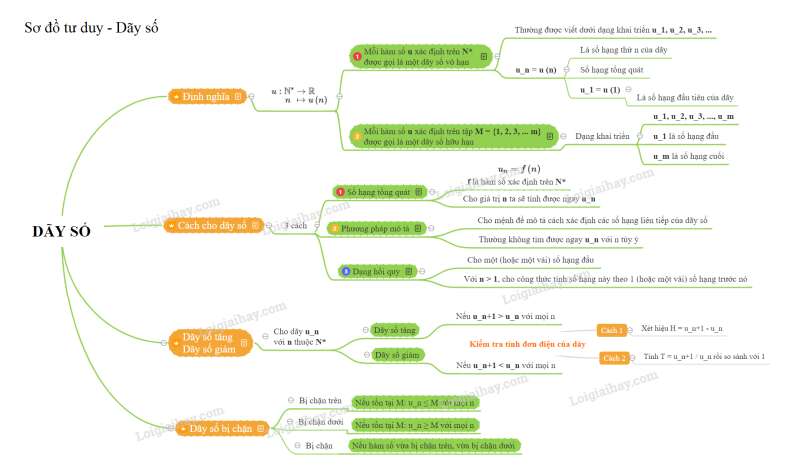
1. Định nghĩa
a) Mỗi hàm số xác định trên tập số nguyên dương * được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:
Dãy số thường được viết dưới dạng khai triển u1, u2,u3, ….,un,….,
trong đó un = u(n) là số hạng thứ n và gọi nó là số hạng tổng quát, u1 là số hạng đầu của dãy số (un )
b) Mỗi hàm số u xác định trên tập M = {1, 2, 3, ..., m}, với được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là: u1, u2,u3, ….,, trong đó u1 là số hạng đầu, là số hạng cuối.
2. Cách cho một dãy số
a) Dãy số cho bằng công thức của số hạng tổng quát.
Khi đó , trong đó f là một hàm số xác định trên
Đây là cách khá thông dụng (giống như hàm số) và nếu biết giá trị của n (hay cũng chính là số thứ tự của số hạng) thì ta có thể tính ngay được .
b) Dãy số cho bằng phương pháp mô tả
Người ta cho một mệnh đề mô tả cách xác định các số hạng liên tiếp của dãy số. Tuy nhiên, thường thì không tìm ngay được với n tuỳ ý.
c) Dãy số cho bằng phương pháp truy hồi (hay quy nạp)
- Cho số hạng thứ nhất (hoặc một vài số hạng đầu).
- Với n ≥ 2, cho một công thức tính nếu biết (hoặc một vài số hạng đứng trước đó)
Chẳng hạn, các công thức có thể là:
hoặc
3. Dãy số tăng, dãy số giảm
- Dãy số được gọi là dãy số tăng nếu un+1 > un với mọi ;
- Dãy số được gọi là dãy số giảm nếu un+1 < un với mọi .
Phương pháp khảo sát tính đơn điệu của dãy số :
Phương pháp 1:
Xét hiệu H = un+1 - un.
- Nếu H > 0 với mọi thì dãy số tăng
- Nếu H < 0 với mọi thì dãy số giảm.
Phương pháp 2:
Nếu un > 0 với mọi thì lập tỉ số , rồi so sánh với 1.
- Nếu với mọi thì dãy số tăng.
- Nếu với mọi thì dãy số giảm.
4. Dãy số bị chặn
- Dãy số được gọi là bị chặn trên nếu tồn tại số M sao cho
≤ M, với mọi
- Dãy số Un được gọi là bị chặn dưới nếu tồn tại số m sao cho
≥ m, với mọi
- Dãy số Un được gọi là bị chặn nếu nó vừa bị chặn trêm vừa bị chặn dưới tức là tồn tại hai số m, M sao cho:
m ≤ ≤ M, với mọi