Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Dãy số (Lý thuyết + 40 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.
Nội dung bài viết
Mời các bạn đón xem:
Dãy số (Lý thuyết + 40 bài tập có lời giải)
I. Lý thuyết Dãy số
I.1 Định nghĩa
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương N* được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:
u: N* → R
n → u(n).
Người ta thường viết dãy số dưới dạng khai triển
u1, u2, u3,…, un,…,
trong đó un = u(n) hoặc viết tắt là (un), và gọi u1 là số hạng đầu, un là số hạng thứ n và là số hạng tổng quát của dãy số.
2. Định nghĩa dãy số hữu hạn
Mỗi hàm số u xác định trên tập M = {1,2,3,…,m} với m ∈ N* được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là u1, u2, u3,…, un, trong đó u1 là số hạng đầu, un là số hạng cuối.
1. Dãy số cho bằng công thức của số hạng tổng quát
2. Dãy số cho bằng phương pháp mô tả
3. Dãy số cho bằng phương pháp truy hồi
Cách cho một dãy số bằng phương pháp truy hồi, tức là:
a) Cho số hạng đầu (hay vài số hạng đầu).
b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
1. Dãy số tăng, dãy số giảm
Định nghĩa 1
Dãy số (un) được gọi là dãy số tăng nếu ta có un+1 > un với mọi n ∈ N*.
Dãy số (un) được gọi là dãy số giảm nếu ta có un+1 < un với mọi n ∈ N*.
Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số (un) với un = (–3)n tức là dãy –3; 9; –27; 81,… không tăng cũng không giảm.
2. Dãy số bị chặn
Định nghĩa 2
Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho
un ≤ M, ∀ n ∈ N*
Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho
un ≥ m, ∀ n ∈ N*
Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho
m ≤ un ≤ M, ∀ n ∈ N*
Câu 1: Cho dãy số có 4 số hạng đầu là: −1,3,19,53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.
A. u10=97
B. u10=71
C. u10=1414
D. u10=971
Đáp án: A
Câu 2: Cho dãy số (un)với un=an2n+1 (a: hằng số). un+1 là số hạng nào sau đây?
A. un+1=a.(n+1)2n+2.
B. un+1=a.(n+1)2n+1.
C. un+1=a.n2+1n+1.
D. un+1=an2n+2.
Đáp án: A
Câu 3: Cho dãy số có các số hạng đầu là: 5;10;15;20;25;...Số hạng tổng quát của dãy số này là:
A. un=5(n−1).
B. un=5n.
C. un=5+n.
D. un=5.n+1.
Đáp án: B
Câu 4: Cho dãy số có các số hạng đầu là:8,15,22,29,36,....Số hạng tổng quát của dãy số này là:
A. un=7n+7
B. un=7.n
C. un=7.n+1
D. un : Không viết được dưới dạng công thức
Đáp án: C
Câu 5: Cho dãy số có các số hạng đầu là: 0;12;23;34;45;.... Số hạng tổng quát của dãy số này là:
A. un=n+1n
B. un=nn+1
C. un=n−1n
D. un=n2−nn+1
Đáp án: B
Câu 6: Cho dãy số có các số hạng đầu là: −2;0;2;4;6;.... Số hạng tổng quát của dãy số này có dạng?
A. un=−2n
B. un=(−2)+n
C. un=(−2)(n+1)
D. un=(−2)+2(n−1)
Đáp án: D
Câu 7: Xét tính tăng, giảm và bị chặn của dãy số (un), biết: un=2n−133n−2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Đáp án: A
Câu 8: Cho dãy số được xác định như sau: {u1=1un=3un−1+12un−1−2, n≥2.
Viết 4 số hạng đầu của dãy và chứng minh rằng un>0, ∀n
A. u1=1,u2=32,u3=476,u4=22734
B. u1=1,u2=32,u3=176,u4=22734
C. u1=1,u2=32,u3=196,u4=22734
D. u1=1,u2=32,u3=176,u4=212734
Đáp án: B
Câu 9: Cho dãy số có các số hạng đầu là: 13;132;133;134;135;…. Số hạng tổng quát của dãy số này là?
A. un=1313n+1
B. un=13n+1
C. un=13n
D. un=13n−1
Đáp án: C
Câu 10: Cho dãy số (un) với {u1=5un+1=un+n. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=(n−1)n2
B. un=5+(n−1)n2
C. un=5+(n+1)n2
D. un=5+(n+1)(n+2)2
Đáp án: B
Câu 11: Cho dãy số (un) với {u1=1un+1=un+(−1)2n. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=1+n
B. un=1−n
C. un=1+(−1)2n
D. un=n
Đáp án: D
Câu 12: Cho dãy số (un) với {u1=1un+1=un+(−1)2n+1. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=2−n.
B. un không xác định.
C. un=1−n.
D. un=−n với mọi n.
Đáp án: A
Câu 13: Xét tính tăng giảm của các dãy số sau: un=3n2−2n+1n+1
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: B
Câu 14: Xét tính tăng giảm của các dãy số sau: un=n−√n2−1
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: B
Câu 15: Cho dãy số (un) với {u1=1un+1=un+n2. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=1+n(n+1)(2n+1)6
B. un=1+n(n−1)(2n+2)6
C. un=1+n(n−1)(2n−1)6
D. un=1+n(n+1)(2n−2)6
Đáp án: C
Câu 16: Cho dãy số (un) với {u1=2un+1−un=2n−1. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=2+(n−1)2.
B. un=2+n2.
C. un=2+(n+1)2.
D. un=2−(n−1)2.
Đáp án: A
Câu 17: Cho dãy số (un) với {u1=−2un+1=−2−1un. Công thức số hạng tổng quát của dãy số này là:
A. un=−n−1n
B. un=n+1n
C. un=−n+1n
D. un=−nn+1
Đáp án: C
Câu 18: Cho dãy số (un) với {u1=12un+1=un−2. Công thức số hạng tổng quát của dãy số này là:
A. un=12+2(n−1).
B. un=12−2(n−1).
C. un=12−2n.
D. un=12+2n.
Đáp án: B
Câu 19: Xét tính tăng giảm của các dãy số sau: un=3n−12n
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: A
Câu 20: Xét tính tăng giảm của các dãy số sau: un=n+(−1)nn2
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: C
Câu 21: Cho dãy số (un) được xác định bởi : {u0=2011un+1=u2nun+1, ∀n=1,2,...
Khẳng định nào sau đây đúng
A. Dãy (un) là dãy giảm
B. Dãy (un) là dãy tăng
C. Dãy (un) là dãy không tăng, không giảm
D. A, B, C đều sai
Đáp án: A
Câu 22: Cho dãy số (un) với 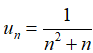 .Khẳng định nào sau đây là sai?
.Khẳng định nào sau đây là sai?
A. Năm số hạng đầu của dãy là: 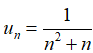 ;
;
B. Là dãy số tăng.
C. Bị chặn trên bởi số M = 1/2.
D. Không bị chặn.
Đáp án: B
Câu 23: Cho dãy số có các số hạng đầu là: 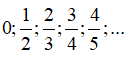 .Số hạng tổng quát của dãy số này là:
.Số hạng tổng quát của dãy số này là:
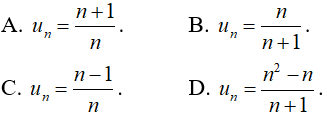
Đáp án: B
Câu 24: Xét tính tăng giảm của các dãy số sau: 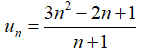
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: A
Câu 25: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
A. 1, 6
B. 6
C. 0,5
D. 0,6
Đáp án: C
Câu 26: Cho cấp số cộng (un) thỏa mãn: 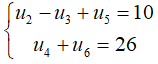 Xác định công sai d
Xác định công sai d
A. d = 2
B. d = 4
C. d = 3
D. d = 5
Đáp án: C
Câu 27: Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d = 2. Tìm n?
A. n = 12
B. n = 13
C. n = 14
D. n = 15
Đáp án: A
Câu 28 : Nếu các số 5 + m; 7 + 2m; 17 + m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
A. m = 2
B. m = 3
C. m = 4
D. m = 5
Đáp án: C
Câu 29: Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng.
A. un = 5n + 1
B. un = 5n - 1
C. un = 4n + 1
D. un = 4n - 1
Đáp án: C
Câu 30: Cho cấp số cộng (un) có d = -2 và S8 = 72. Tìm số hạng đầu tiên u1?
A. 16
B. –16
C. 4
D. 8
Đáp án: A
Câu 31: Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu?
A. d = 2
B. d = 3
C. d = 4
D. d = 5
Đáp án: A
Câu 32: Cho cấp số cộng (un) thỏa mãn u2 + u23 = 60. Tính tổng S24 của 24 số hạng đầu tiên của cấp số cộng đã cho.
A. 60
B. 120
C. 720
D. 1440
Đáp án: C
Câu 33: Cho cấp số cộng (un) thỏa mãn 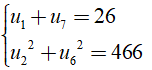 .Mệnh đề nào sau đây đúng?
.Mệnh đề nào sau đây đúng?
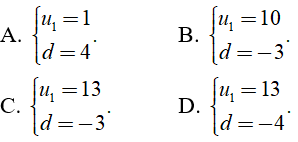
Đáp án: A
Câu 34: Trong các dãy số (un) sau, dãy nào là cấp số nhân?
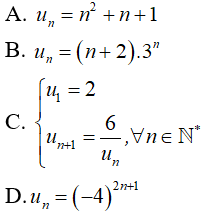
Đáp án: D
Câu 35: Cho cấp số nhân (un) với công bội q < 0 và u2 = 4, u4 = 9. Tìm u1 .
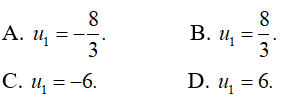
Đáp án: A
Câu 36: Cho cấp số nhân (un) biết u1 + u5 = 51; u2 + u6 = 102. Hỏi số 12288 là số hạng thứ mấy của cấp số nhân (un) ?
A. Số hạng thứ 10.
B. Số hạng thứ 11.
C. Số hạng thứ 12.
D. Số hạng thứ 13.
Đáp án: D
Câu 37: Tìm x biết 1, x2, 6 - x2 lập thành cấp số nhân.
A. x = ± 1
B. x = ± 1
C. x = ± √2
D. x = ± √3
Đáp án: B
Câu 38: Tính tổng tất cả các số hạng của một cấp số nhân , biết số hạng đầu bằng 18, số hạng thứ hai bằng 54 và số hạng cuối bằng 39366.
A. 19674.
B. 59040.
C. 177138.
D. 6552
Đáp án: B
Câu 39: Các số x + 6y ; 5x + 2y; 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x- 1 ; y + 2 ; x – 3y theo thứ tự đó lập thành một cấp số nhân. Tính x2 + y2
A. 40
B. 25
C. 100
D. 10
Đáp án: A
Câu 40: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
Đáp án: D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.