Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Phương pháp quy nạp toán học (Lý thuyết + 40 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Phương pháp quy nạp toán học (Lý thuyết + 40 bài tập có lời giải)
I. Lý thuyết Phương pháp quy nạp toán học
1. Để chứng minh một mệnh đề là đúng với mọi n ∈ ℕ* bằng phương pháp quy nạp toán học, ta tiến hành hai bước:
♦ Bước 1: Kiểm tra rằng mệnh đề đúng với n = 1.
♦ Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k (k ≥ 1) (ta gọi là giả thiết quy nạp) và chứng minh rằng nó cũng đúng với n=k+1.
2. Trong trường hợp phải chứng minh một mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là số tự nhiên) thì:
♦ Ở bước 1, ta kiểm tra mệnh đề đúng với n = p.
♦ Ở bước 2, ta giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k (k ≥ p) và chứng minh rằng nó cũng đúng với n = k + 1.
3. Phép thử với một số hữu hạn số tự nhiên, tuy không phải là chứng minh, nhưng cho phép ta dự đoán được kết quả. Kết quả này chỉ là giả thiết, và để chứng minh ta có thể dùng phương pháp quy nạp toán học.
II. Bài tập Phương pháp quy nạp toán học
Câu 1. Với mọi số tự nhiên n , tổng Sn=n3+3n2+5n+3 chia hết cho:
A. 3
B. 4
C. 5
D. 7
Đáp án: A
Câu 2. Giá trị của tổng là:
S=1−2+3−4+...−2n+(2n+1)
A. 1
B. 0
C. 5
D. n +1
Đáp án: D
Câu 3. Với mọi số nguyên dương n , tổng Sn=1.2+2.3+3.4+...+n(n+1) là:
A. n(n+1)(n+2)(n+3)6
B. n(n+1)(n+2)3
C. n(n+1)(n+2)2
D. Đáp số khác
Đáp án: B
Câu 4: Một học sinh chứng minh mệnh đề ''8n+1 chia hết cho 7,∀n∈N*''(*) như sau:
Giả sử (*) đúng với n=k tức là 8k+ 1 chia hết cho 7
Ta có: 8k+ 1 = 8(8k+1)- 7, kết hợp với giả thiết 8k+ 1 chia hết cho 7 nên suy ra được 8k+1+ 1 chia hết cho 7.
Vậy đẳng thức (*) đúng với mọi n∈N*
Khẳng định nào sau đây là đúng?
A. Học sinh trên chứng minh đúng.
B. Học sinh chứng minh sai vì không có giả thiết qui nạp.
C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.
D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp
Đáp án: D
Câu 5: Với n∈N* , ta xét các mệnh đề: P :“ 7n + 5 chia hết cho 2”;
Q: “7n+ 5 chia hết cho 3” và R: “7n+ 5 chia hết cho 6”.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 3
B. 0
C. 1
D. 2
Đáp án: A
Câu 6: Trong phương pháp quy nạp toán học, nếu ta giả sử mệnh đề đúng với n=k thì ta cần chứng minh mệnh đề đúng đến:
A. n=k−1
B. n=k−2
C. n=k+1
D. n=k+2
Đáp án: C
Câu 7: Đối với bài toán chứng minh P(n) đúng với mọi n≥p với p là số tự nhiên cho trước thì ở bước 1 ta cần chứng minh mệnh đề đúng với:
A. n=1
B. n=k
C. n=k+1
D. n=p
Đáp án: D
Câu 8: Dùng quy nạp chứng minh mệnh đề chứa biến P(n) đúng với mọi số tự nhiên n≥p (p là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề P(n) đúng với n=k. Khẳng định nào sau đây là đúng?
A. k≠p
B. k≥p
C. k=p
D. k<p
Đáp án: B
Câu 9: Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến đúng với mọi số tự nhiên n≥p ( p là một số tự nhiên), ta tiến hành hai bước:
- Bước 1, kiểm tra mệnh đề P(n) đúng với n=p
- Bước 2, giả thiết mệnh đề P(n) đúng với số tự nhiên bất kỳ n=k≥p và phải chứng minh rằng nó cũng đúng với n=k+1
Trong hai bước trên:
A. Chỉ có bước 1 đúng.
B. Chỉ có bước 2 đúng.
C. Cả hai bước đều đúng
D. Cả hai bước đều sai
Đáp án: C
Câu 10: Trong phương pháp quy nạp toán học, ở bước 2, nếu ta giả sử mệnh đề đúng với n=k+1 thì ta cần chứng minh mệnh đề đúng với:
A. n=k
B. n=k+1
C. n=k+2
D. n=k+3
Đáp án: B
Câu 11: Giả sử Q là tập con thật sự của tập hợp các số nguyên dương sao cho
a) k∈Q
b) n∈Q⇒n+1∈Q∀n≥k
Chọn mệnh đề đúng trong các mệnh đề sau.
A. Mọi số nguyên dương đều thuộc Q.
B. Mọi số nguyên dương lớn hơn hoặc bằng k đều thuộc Q.
C. Mọi số nguyên bé hơn k đều thuộc Q.
D. Mọi số nguyên đều thuộc Q.
Đáp án: B
Câu 12. Tìm số nguyên dương p nhỏ nhất để 2n>2n+1 với mọi số nguyên
A. p = 5
B. p = 3
C. p = 4
D. p = 2
Đáp án: B
Câu 13: Với mọi số nguyên dương n, tổng 2 + 5 + 8 + … + (3n – 1) là:
A. n(3n+1)2
B. n(3n−1)2
C. n(3n+2)2
D. 3n22
Đáp án: A
Câu 14: Với mọi số nguyên dương n≥2, ta có: (1−14)(1−19)...(1−1n2)=an+2bn, trong đó a, b là các số nguyên. Tính các giá trị của biểu thức T=a2+b2
A. P = 5
B. P = 9
C. P = 20
D. P = 36
Đáp án: C
Câu 15: So sánh an+bn2và (a+b2)n, với a≥0;b≥0,n∈N* ta được:
A. an+bn2<(a+b2)n
B. an+bn2≥(a+b2)n
C. an+bn2=(a+b2)n
D. Không so sánh được
Đáp án: B
Câu 16: Với mỗi số nguyên dương n , đặt S=12+22+...+n2. Mệnh đề nào dưới đây là đúng
A. S=n(n+1)(n+2)6
B. S=n(n+1)(2n+2)3
C. S=n(n+1)(2n+1)6
D. S=n(n+1)(n+2)6
Đáp án: C
Câu 17: Với mọi số tự nhiên n≥2 bất đẳng thức nào sau đây đúng?
A. 3n>4n+1
B. 3n>4n+2
C. 3n>3n+2
D. Cả ba đều đúng
Đáp án: C
Câu 18. Tính tổng:
1.4 + 2.7 + … +n.(3n +1)
A. n.(n+1)2
B. (n+1).(n+2)2
C. (n+1).(2n−3)2
D. Đáp án khác
Đáp án: A
Câu 19. Chứng minh n3+3n2+5n chia hết cho 3
Đáp án:
Đặt un= n3+3n2+5n
Ta có u1=13+3.12+5.1=9 chia hết cho 3.
Giả sử uk= k3+3k2+5k chia hết cho 3.
Ta cần chứng minh
uk+1=(k+1)3+3(k+1)2+5(k+1) chia hết cho 3.
Thật vậy, ta có:
uk+1
=k3+3k2+3k+1+3k2+6k+3
+5k+5
=k3+ 6k2+ 14k+9
=(k3+3k+25k)
+ (3k2+ 9k+ 9)
=uk+3(k2+3k+3).
Vì uk và 3(k2+3k+3) đều chia hết cho 3, nên uk+1 cũng chia hết cho 3.
Vậy với mọi số nguyên dương n thì un chia hết cho 3.
Câu 20: Tìm tất cả các số nguyên dương n sao cho 2n+1>n2+3n
A. n≥3
B. n≥5
C. n≥6
D. n≥4
Đáp án: D
Câu 21: Cho tổng Sn=11.2+12.3+13.4+...+1n(n+1). Mệnh đề nào đúng?
A. Sn=1n+1
B. Sn=nn+1
C. Sn=n+1n+2
D. Sn=nn+2
Đáp án: B
Câu 22: Đặt Sn=11.3+13.5+...+1(2n−1)(2n+1) với n∈N*. Mệnh đề nào dưới đây đúng
A. Sn=n+12(2n+1)
B. Sn=3n−14n+2
C. Sn=n+26n+3
D. Sn=n2n+1
Đáp án: C
Câu 23: Với n∈N*, hãy rút gọn biểu thức
S=1.4+2.7+...+n(3n+1)
A. S=n(n+1)2
B. S=n(n+2)2
C. S=n(n+1)
D. S=2n(n+1)
Đáp án: A
Câu 24. Kí hiệu k!=k(k−1)...2.1,∀k∈N* đặt Sn=1.1!+2.2!+...+n.n! Mệnh đề nào dưới đây là đúng?
A. Sn=2.n!
B. Sn=(n+1)!−1
C. Sn=(n+1)!
D. Sn=(n+1)!+1
Đáp án: B
Câu 25: Chọn mệnh đề đúng: Với mọi n∈N* thì:
A. (13n−1)⋮13
B. (13n−1)⋮8
C. (13n−1)⋮12
D. (13n−1)⋮7
Đáp án: C
Câu 26: Bất đẳng thức nào sau đây đúng? Với mọi số tự nhiên n thỏa n≥3 thì:
A. 2n<n
B. 2n<2n
C. 2n<n+1
D. 2n>2n+1
Đáp án: D
Câu 27. Bất đẳng thức nào sau đây đúng? Với mọi số nguyên dương n thì:
A. 1+1√2+...+1√n>2√n
B. 1+1√2+...+1√n>3√n
C. 1+1√2+...+1√n<2√n
D. 1+1√2+...+1√n>4√5
Đáp án: C
Câu 28: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau 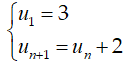
A. un = 3n + n2 -1
B. un = 2n + 1
C. un = 4n - 10
D. Đáp án khác
Đáp án: A
Câu 29: Xét tính tăng giảm của dãy số (un) biết: 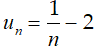
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Dãy số không đổi.
Đáp án: B
Câu 30: Xét tính tăng hay giảm và bị chặn của dãy số : 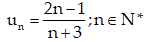
A. Dãy số giảm, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số tăng, bị chặn.
D. Dãy số giảm, bị chặn dưới.
Đáp án: C
Câu 31: Cho dãy số (un) có số hạng tổng quát 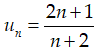 . Số 167/84 là số hạng thứ mấy?
. Số 167/84 là số hạng thứ mấy?
A. 300.
B. 212.
C. 250.
D. 249.
Câu 32: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau 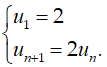
A. un = n2 - 3n + 10
B. un = 2n
C. un = 2n
D. un = n + 2
Câu 33: Xét tính tăng giảm của dãy số (un) biết: 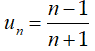
A. Dãy số giảm.
B. Dãy số không tăng không giảm
C. Dãy số không đổi.
D. Dãy số tăng
Câu 34: Cho dãy số 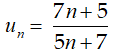 . Tìm mệnh đề đúng?
. Tìm mệnh đề đúng?
A. Dãy số tăng và bị chặn.
B. Dãy số giảm và bị chặn.
C. Dãy số tăng và bị chặn dưới
D. Dãy số giảm và bị chặn trên.
Câu 35: Xét tính bị chặn của dãy số (un) biết: 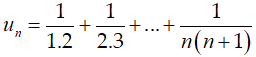
A. Dãy số bị chặn trên
B. Dãy số bị chặn dưới.
C. Dãy số bị chặn
D. Tất cả sai.
Câu 36: Cho dãy số (un) xác định bởi 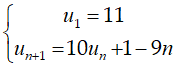 . Tìm số hạng tổng quát un theo n.
. Tìm số hạng tổng quát un theo n.
A. un = 100 + 2n
B.un = 10n + n
C. un = 100n – n2
D. Đáp án khác
Câu 37: Xét tính tăng giảm của dãy số (un) với 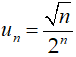
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Dãy số không đổi.
Đáp án: B
Câu 38: Cho dãy số (un) biết 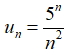 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Dãy số là dãy hữu hạn
Đáp án: A
Câu 39: Cho dãy số (un) biết 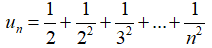 . Mệnh đề nào sau đây đúng ?
. Mệnh đề nào sau đây đúng ?
A. Dãy số bị chặn dưới.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn.
D. Không bị chặn
Câu 40: Xét tính tăng, giảm và bị chặn của dãy số (un), biết: 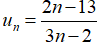
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.