Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Ôn tập chương 5 (Lý thuyết + 35 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Ôn tập chương 5 (Lý thuyết + 35 bài tập có lời giải)

A. Lý thuyết Ôn tập chương 5

ĐỊNH NGHĨA VÀ Ý NGHĨA ĐẠO HÀM

I. ĐẠO HÀM TẠI MỘT ĐIỂM

1. Định nghĩa đạo hàm tại một điểm

    Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Nếu tồn tại giới hạn (hữu hạn)

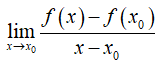
thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x₀ và kí hiệu là f’(x₀) (hoặc y’(x₀)), tức là

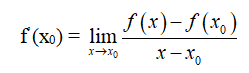
Chú ý:

    Đại lượng Δx = x – x₀ gọi là số gia của đối số x tại x₀.

    Đại lượng Δy = f(x) – f(x₀) = f(x₀ + Δx) – f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy

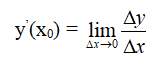
2. Cách tính đạo hàm bằng định nghĩa

    Bước 1. Giả sử Δx là số gia của đối số x tại x₀, tính Δy = f(x₀ + Δx) – f(x₀).

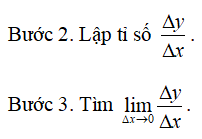
3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lí 1

    Nếu hàm số y = f(x) có đạo hàm tại x₀ thì nó liên tục tại x₀.

Chú ý:

    a) Nếu y = f(x) gián đoạn tại x₀ thì nó không có đạo hàm tại x₀.

    b) Nếu y = f(x) liên tục tại x₀ thì có thể không có đạo hàm tại x₀.

4. Ý nghĩa hình học của đạo hàm

Định lí 2

Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến M0T của đồ thị hàm số tại điểm M0(x0; f(x0)).

Định lí 3

Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M0(x0; f(x0)) là

y – y0 = f’(x0)(x – x0)

trong đó y0 = f(x0).

5. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời: v(t0) = s’(t0).

Cường độ tức thời: I(t0) = Q’(t0).

II. ĐẠO HÀM TRÊN MỘT KHOẢNG

Định nghĩa

    Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

    Khi đó, ta gọi hàm số f’: (a; b) → R

    x → f’(x)

    là đạo hàm của hàm số y = f(x) trên khoảng (a; b), kí hiệu là y’ hay f’(x).

QUY TẮC TÍNH ĐẠO HÀM

I. ĐẠO HÀM CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP

Định lí 1

    Hàm số y = xⁿ (n ∈ N, n > 1) có đạo hàm tại mọi x ∈ R và (xⁿ)’ = nx^{n – 1}

Định lí 2

    Hàm số y = √x có đạo hàm tại mọi x dương và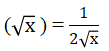 

II. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG

1. Định lí

Định lí 3

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có

    (u + v)’ = u’ + v’

    (u – v)’ = u’ – v’

    (uv)’ = u’v – v’u

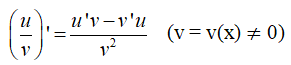
Hệ quả 1

    Nếu k là một hằng số thì (ku)’ = ku’.

Hệ quả 2

III. ĐẠO HÀM CỦA HÀM HỢP

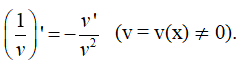
Định lí 4

    Nếu hàm số u = g(x) có đạo hàm tại x là u'_x và hàm số y = f(u) có đạo hàm tại u là y'_u thì hàm hợp y = f(g(x)) có đạo hàm tại x là y'_x = y'_u.u'_x .

ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC

1. Giới hạn của 

Định lý 1

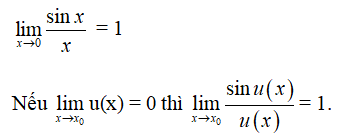
2. Đạo hàm của hàm số y = sinx

Định lý 2

    Hàm số y = sin x có đạo hàm tại mọi x ∈ R và (sin x)’ = cosx.

    Nếu y = sin u và u = u(x) thì (sin u)’ = u’.cos u.

3. Đạo hàm của hàm số y = cos x

Định lý 3

    Hàm số y = cos x có đạo hàm tại mọi x ∈ R và (cos x)’ = –sin x .

    Nếu y = cos u và u = u(x) thì (cos u)’ = –u’.sin u

4. Đạo hàm của hàm số y = tan x

Định lý 4

    Hàm số y = tan x có đạo hàm tại mọi x ≠ π/2 + kπ và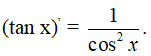 

    Nếu y = tan u và u = u(x) thì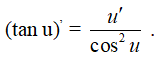 

5. Đạo hàm của hàm số y = cot x

Định lý 5

    Hàm số y = cot x có đạo hàm tại mọi x ≠ kπ và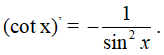 

    Nếu y = cot u và u = u(x) thì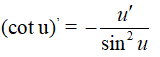 

VI PHÂN

Cho hàm số f^(n–1)(x) xác định trên khoảng (a; b) và có đạo hàm tại x ∈ (a; b). Giả sử f^(n–1)(x) (n ∈ N, n ≥ 4) là số gia của x.

Ta gọi tích f’(x₀)Δx là vi phân của hàm số n – 1 tại x ứng với số gia Δx, kí hiệu là y = f(x) hoặc dy, tức là

        dy = df(x) = f’(x)Δx

ĐẠO HÀM CẤP HAI

1. Định nghĩa

    Giả sử hàm số y = f(x) có đạo hàm tại mỗi điểm x ∈ (a;b). Khi đó, hệ thức y’ = f’(x) xác định một hàm số mới trên khoảng (a; b). Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) và kí hiệu là y’’ hoặc f’’(x).

Chú ý:

    + Đạo hàm cấp 3 của hàm số y = f(x) được định nghĩa tương tự và kí hiệu là y’’’ hoặc f’’’(x) hoặc f⁽³⁾(x).

    + Cho hàm số y = f(x) có đạo hàm cấp n – 1 , kí hiệu f^(n–1)(x) (n ∈ N, n ≥ 4). Nếu f^(n–1)(x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f(x), kí hiệu y⁽ⁿ⁾ hoặc f⁽ⁿ⁾(x).

            f⁽ⁿ⁾(x) = (f^(n–1)(x))’

2. Ý nghĩa cơ học của đạo hàm cấp hai

    Đạo hàm cấp hai f’’(t) là gia tốc tức thời của chuyển động s = f(t) tại thời điểm t.

B. Bài tập Ôn tập chương 5

Câu 1: Đạo hàm của hàm số $f\left(x\right)=2x+1$ tại $x_0=1$ là

A. 2.

B. 3.

C. 4.

D. 5.

Đáp án: A

Câu 2: Vi phân của hàm số $y=2x^5-\frac{2}{x}+5$ là biểu thức nào dưới đây?

A. $\left(10x^4-\frac{2}{x^2}\right)dx.$

B. $\left(10x^4+\frac{2}{x^2}+5\right)dx.$

C. $\left(10x+\frac{2}{x^2}\right)dx.$

D. $\left(10x^4+\frac{2}{x^2}\right)dx.$   

Đáp án: D

Câu 3: Cho hàm số $y=f\left(x\right)$ có đồ thị $\left(C\right)$ và điểm $M\left(x_0;y_0\right)\in \left(C\right)$. Khi đó, tiếp tuyến của $\left(C\right)$ tại điểm M có hệ số góc là

A. $f^{\text{'}}\left(x_0\right)$

B. $f^{\text{'}}\left(x\right).$

C. $f^{\text{'}}\left(x-x_0\right).$

D. $f^{\text{'}}\left(x+x_0\right).$

Đáp án: A

Câu 4: Đạo hàm của hàm số $y=\sqrt{x}$ là

A. $y^{\text{'}}=\frac{2}{\sqrt{x}}.$

B. $y^{\text{'}}=\frac{1}{\sqrt{x}}.$

C. $y^{\text{'}}=\frac{1}{2\sqrt{x}}.$

D. $y^{\text{'}}=2\sqrt{x}.$

Đáp án: C

Câu 5: Đạo hàm của hàm số $y=\cos x$ là

A.$y^{\text{'}}=\sin x.$

B. $y^{\text{'}}=\tan x.$

C. $y^{\text{'}}=\frac{1}{{\tan }^{2}x}.$

D.  $y^{\text{'}}=-\sin x.$

Đáp án: D

Câu 6: Hàm số $y=\sin x+x$ có đạo hàm là

A. $-\cos x+1.$

B. $\cos x+1.$

C. $\sin x+x.$

D.  $\sin x+1.$

Đáp án: B

Câu 7: Đâu là phương trình tiếp tuyến của đồ thị hàm số $y=f\left(x\right)$ tại điểm $M\left(x_0;y_0\right)$?

A. $y-y_0=f\left(x_0\right)\left(x-x_0\right).$

B. $y=f\left(x_0\right)\left(x-x_0\right)+y_0.$

C. $y+y_0=f^{\text{'}}\left(x_0\right)\left(x-x_0\right).$

D. $y=f^{\text{'}}\left(x_0\right)\left(x-x_0\right)+y_0.$

Đáp án: D

Câu 8: Tính đạo hàm của hàm số  $y=x^2+1$

A. $y^{\text{'}}=x^2+1.$

B. $y^{\text{'}}=2x+1.$

C. $y^{\text{'}}=2x.$

D. $y^{\text{'}}=2x-1.$

Đáp án: C

Câu 9: Cho hàm số $y=\sin x$. Tính $y^{\text{'}\text{'}}\left(0\right)$

A. $y^{\text{'}\text{'}}\left(0\right)=0.$

B. $y^{\text{'}\text{'}}\left(0\right)=1.$

C. $y^{\text{'}\text{'}}\left(0\right)=2.$

D. $y^{\text{'}\text{'}}\left(0\right)=-2.$

Đáp án: A

Câu 10: Cho hàm số $y=f\left(x\right)$ có đạo hàm trên tập số thực. Tìm hệ thức đúng.

A. $f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}.$

B. $f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)}{x-1}.$

C. $f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)}{x}.$

D. $f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(1\right)}{x-1}.$

Đáp án: A

Câu 11: Cho hàm số y= f (x)  có đạo hàm đến cấp 2 trên tập số thực. Tìm hệ thức đúng.

A. $f^{\text{'}\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}.$

B. $f^{\text{'}\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f^{\text{'}}\left(x\right)-f^{\text{'}}\left(1\right)}{x-1}.$

C. $f^{\text{'}\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)}{x}.$

D. $f^{\text{'}\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(1\right)}{x-1}.$

Đáp án: B

Câu 12: Lập phương trình tiếp tuyến của đồ thị hàm số $y=x^2+3x+1$ tại điểm có hoành độ bằng 1.

A. $y=5x.$

B. $y=5x+5.$

C. $y=5x-5.$

D. $y=x.$

Đáp án: A

Câu 13: Cho chuyển động thẳng xác định bởi phương trình: $S\left(t\right)=t^3+3t^2-9t+27$, trong đó t tính bằng giây  và S được tính bằng mét. Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là

A. $0{\text{\hspace{0.17em}\hspace{0.17em}m/s}}^{\text{2}}\text{.}$

B. $6{\text{\hspace{0.17em}\hspace{0.17em}m/s}}^{\text{2}}\text{.}$

C. ${\text{24\hspace{0.17em}\hspace{0.17em}m/s}}^{\text{2}}\text{.}$

D. ${\text{12\hspace{0.17em}\hspace{0.17em}m/s}}^{\text{2}}\text{.}$

Đáp án: D

Câu 14: Cho hàm số $y=\frac{1}{2}{x}^4-mx-\frac{3}{x}$. Có bao nhiêu giá trị nguyên dương của tham số m để $y^{\text{'}}\ge 0$ với mọi x thuộc khoảng $\left(0;+\infty \right)$?

A. 5.

B. 3.

C. 0.

D. 4.

Đáp án: A

Câu 15: Cho hàm số $f\left(x\right)=a{x}^3+\frac{b}{x^3}+c{x}^2$. Biết $f\left(2\right)=\frac{95}{4}$, $f^{\text{'}}\left(1\right)=16$, $f^{\text{'}}\left(-1\right)=8$. Khi đó tính tổng  $a+b+c$

A. 1.

B. 2.

C. 0.

D. 3.

Đáp án: B

Câu 16: Hệ số góc k của tiếp tuyến với đồ thị hàm số $y=\frac{2x+1}{x+1}$ tại giao điểm của đồ thị hàm số với trục tung là?

A. $k=2.$ 

B. $k=-2.$

C. $k=1.$

D. $k=-1.$

Đáp án: C

Câu 17: Một chuyển động có phương trình $s\left(t\right)=t^2-2t+3$ (trong đó s tính bằng mét, t tính bằng giây). Vận tốc tức thời của chuyển động tại thời điểm $t=2s$ là

A. $6\left(\text{m/s}\right).$

B. $4\left(\text{m/s}\right).$

C. $8\left(\text{m/s}\right).$

D. $2\left(\text{m/s}\right).$

Đáp án: A

Câu 18: Cho hàm số $f\left(x\right)=\sqrt{x^2+3}$. Tính giá trị của biểu thức $S=f\left(1\right)+4f^{\text{'}}\left(1\right)$.

A. $S=2.$

B. $S=4.$

C.  $S=6.$

D. $S=8.$

Đáp án: B

Câu 19: Cho hàm số $f\left(x\right)=-x^3+3m{x}^2-12x+3$ với m là tham số thực. Số giá trị nguyên của m để $f^{\text{'}}\left(x\right)\le 0$ với $\forall x\in ℝ$  là

A. 1.

B. 5.

C. 4.

D. 3.

Đáp án: B

Câu 20: Vi phân của hàm số $y=\cos 2x+\cot x$ là

A. $dy=\left(-2\cos 2x+\frac{1}{{\sin }^{2}x}\right)dx.$

B. $dy=\left(2\sin 2x+\frac{1}{{\sin }^{2}x}\right)dx.$

C. $dy=\left(-2\cos 2x-\frac{1}{{\sin }^{2}x}\right)dx.$

D. $dy=\left(-2\sin 2x-\frac{1}{{\sin }^{2}x}\right)dx.$

Đáp án: D

Câu 21: Cho hàm số $f\left(x\right)={\left(2x+1\right)}^{12}$. Tính $f^{\text{'}\text{'}}\left(0\right)$.

A. $f^{\text{'}\text{'}}\left(0\right)=132.$

B. $f^{\text{'}\text{'}}\left(0\right)=528.$

C. $f^{\text{'}\text{'}}\left(0\right)=240.$

D. $f^{\text{'}\text{'}}\left(0\right)=264.$

Đáp án: B

Câu 22: Hệ số góc của tiếp tuyến của đồ thị hàm số $y=\frac{x-1}{x+1}$ tại điểm có hoành độ $x_0=0$ là

A. 1.

B. –2.

C. –1.

D. 2.

Đáp án: D

Câu 23: Tìm số gia $\Delta y$ của hàm số $y=x^2$ biết $x_0=3$ và $\Delta x=-1$.

A. $\Delta y=13.$

B. $\Delta y=7.$

C. $\Delta y=-5.$

D. $\Delta y=16.$

Đáp án: C

Câu 24: Cho hàm số $y=\frac{x^2+3}{x+1}$. Nếu $y^{\text{'}}>0$ thì x thuộc tập hợp nào sau đây:

A. $\left(-\infty ;-3\right)\cup \left(1;+\infty \right).$

B. $\left(-3;-1\right)\cup \left(1;+\infty \right).$

C. $\left(-\infty ;-3\right)\cup \left(-1;1\right).$

D. $\left(-3;-1\right)\cup \left(-1;1\right).$

Đáp án: A

Câu 25: Cho hàm số $y=\cos \sqrt{2x^2-x+7}$. Khi đó $y^{\text{'}}$ bằng

A. $y^{\text{'}}=-\sin \sqrt{2x^2-x+7}.$

B. $y^{\text{'}}=\left(1-4x\right)\sin \sqrt{2x^2-x+7}.$

C. $y^{\text{'}}=\frac{\left(1-4x\right)\sin \sqrt{2x^2-x+7}}{2\sqrt{2x^2-x+7}}.$

D. $y^{\text{'}}=\left(2x^2-x+7\right)\sin \sqrt{2x^2-x+7}$

Đáp án: C

Câu 26: Gọi $\left(C\right)$ là đồ thị của hàm số $y={\left(x-1\right)}^3$. Tiếp tuyến của $\left(C\right)$ song song với đường thẳng $\Delta :12x-y-2018=0$ có phương trình là

A. $y=-12x-4$ và $y=-12x+4$.

B. $y=12x+28$ và $y=12x-4$.

C. $y=-12x-28$ và $y=12x+28$.

D. $y=12x-28$ và $y=12x+4$.

Đáp án: D

Câu 27: Tiếp tuyến của đồ thị hàm số $y=x^3+2x-4$ tại điểm $M\left(0;-4\right)$ có phương trình là

A. $y=2x-2.$

B. $y=2x+4.$

C. $y=2x.$

D. $y=2x-4.$

Đáp án: D

Câu 28: Đạo hàm của hàm số $y=\frac{1}{2}\sin 2x+\cos x$ tại $x_0=\frac{\pi }{2}$ bằng

A. –1.

B. 2.

C. 0.

D. –2.

Đáp án: D

Câu 29: Số gia của hàm số y = x² - 1 tại điểm x₀ = 2 ứng với số gia Δ bằng bao nhiêu?

A. -0,01

B. 0,41

C. 0,99

D. 11,1

Đáp án: B

Câu 30: Cho hàm số 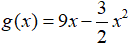. Đạo hàm của hàm số g(x) dương trong trường hợp nào?

A. x < 3

B. x < 6

C. x > 3

D. x < - 3

Câu 31: Cho hai hàm số .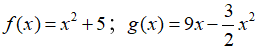

Giá trị của x là bao nhiêu để f'(x) = g'(x)?

A. - 4

B. 4

C. 9/5.

D. 5/9.

Câu 32: Gọi (C) là đồ thị của hàm số y = x³ - 5x² + 2. Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó song song với đường thẳng y = - 3x + 1 .

A. y = -3x – 7

B. y = -3x + 67/27

C. Cả A và B đúng

D. Đáp án khác

Câu 33:  Phương trình tiếp tuyến với đồ thị y = x³ - 2x² + x - 1 tại điểm có hoành độ x₀ = -1 là:

A. y = 8x + 3

B. y = 8x + 7.

C. y = 8x + 8.

D. y = 8x +11

Đáp án: A

Câu 34: Hệ số góc của tiếp tuyến với đồ thị hàm số y = x⁴ + x³ - 2x² + 1 tại điểm có hoành độ -1 là:

A. 11.

B. 4.

C. 3.

D. – 3.

Câu 35: Cho hàm số 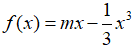. Với giá trị nào của m thì x = -1 là nghiệm của bất phương trình f'(2) < 2?

A. m>3

B. m < 3

C. m = 3

D. m < 1

Đáp án: B