Hệ tọa độ trong không gian + (Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

1. Hệ trục tọa độ trong không gian

    Trong không gian, xét ba trục tọa độ Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi i→, j→, k→ là các vectơ đơn vị, tương ứng trên các trục Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ trục tọa độ vuông góc trong không gian.

    Chú ý: 

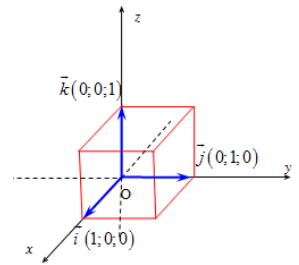
2. Tọa độ của vectơ

    a) Định nghĩa: u→ = (x; y; z) ⇔ k→ = xi→ + yj→ + zk→

    b) Tính chất: Cho a→ = (a₁; a₂; a₃), b→ = (b₁; b₂; b₃), k ∈ R

    • a→ ± b→ = (a₁ ± b₁; a₂ ± b₂; a₃ ± b₃; )

    • ka→ = (ka₁; ka₂; ka₃)

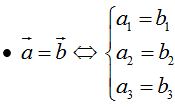
    • 0→ = (0; 0; 0), i→ = (1; 0; 0), j→ = (0; 1; 0), k→ = (0; 0; 1)

    • a→ cùng phương b→ (b→ ≠ 0→) ⇔ a→ = kb→ (k ∈ R)

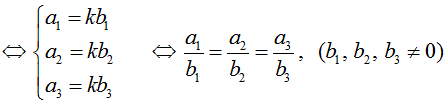
    • a→.b→ = a₁.b₁ + a₂.b₂ + a₃.b₃

    • a→ ⊥ b→ ⇔ a₁b₁ + a₂b₂ + a₃b₃ = 0

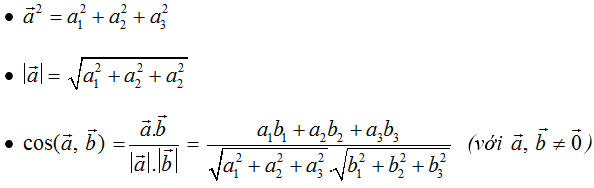
3. Tọa độ của điểm

    a) Định nghĩa: M(x; y; z) ⇔ OM→ = x.i→ + y.j→ + z.k→ (x : hoành độ, y : tung độ, z : cao độ)

    Chú ý: • M ∈ (Oxy) ⇔ z = 0; M ∈ (Oyz) ⇔ x = 0; M ∈ (Oxz) ⇔ y = 0

    • M ∈ Ox ⇔ y = z = 0; M ∈ Oy ⇔ x = z = 0; M ∈ Oz ⇔ x = y = 0 .

    b) Tính chất: Cho A(x_A; y_A; z_A), B(x_B; y_B; z_B)

    • AB→ = (x_B - x_A; y_B - y_A; z_B - z_A)

    • Toạ độ trung điểm của đoạn thẳng AB:

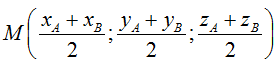
    • Toạ độ trọng tâm G của tam giác ABC:

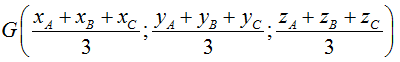
    • Toạ độ trọng tâm G của tứ diện ABCD:

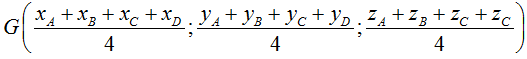
4. Tích có hướng của hai vectơ

    a) Định nghĩa: Trong không gian Oxyz cho hai vectơ a→ = (a₁; a₂; a₃), b→ = (b₁; b₂; b₃). Tích có hướng của hai vectơ a→ và b→ kí hiệu là [a→, b→], được xác định bởi

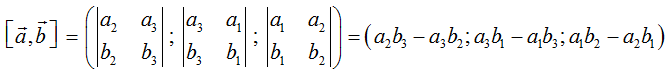
    Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

    b) Tính chất:

    • [a→, b→] ⊥ a→; [a→, b→] ⊥ b→

    • [a→, b→] = -[b→, a→]

    • [i→, j→] = k→; [j→, k→] = i→; [k→, i→] = j→

    • |[a→, b→]| = |a→|.|b→|.sin(a→, b→) (Chương trình nâng cao)

    • a→, b→ cùng phương ⇔ [a→, b→] = 0→ (chứng minh 3 điểm thẳng hàng)

    c) Ứng dụng của tích có hướng: (Chương trình nâng cao)

    • Điều kiện đồng phẳng của ba vectơ: a→, b→ và c→ đồng phẳng ⇔ [a→, b→].c→ = 0

    • Diện tích hình bình hành ABCD: S_ABCD = |[AB→], AD→|

    • Diện tích tam giác ABC: S_ABC = 1/2 |[AB→], AC→|

    • Thể tích khối hộp ABCDA'B'C'D' : V_{ABCD.A'B'C'D'} = |[AB→, AD→].AA'→|

    • Thể tích tứ diện ABCD: V_ABCD = 1/6 |[AB→, AC→].AD→|

    Chú ý:

    – Tích vô hướng của hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính góc giữa hai đường thẳng.

    – Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.

5. Phương trình mặt cầu

    a) Định nghĩa:

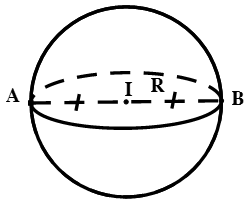
    Cho điểm I cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách I một khoảng R được gọi là mặt cầu tâm I, bán kính R.

    Kí hiệu: S(I; R) ⇔ S(I; R) = {M|IM = R}

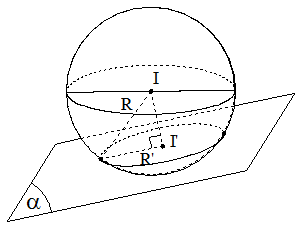
    b) Vị trí tương đối giữa mặt cầu và mặt phẳng :

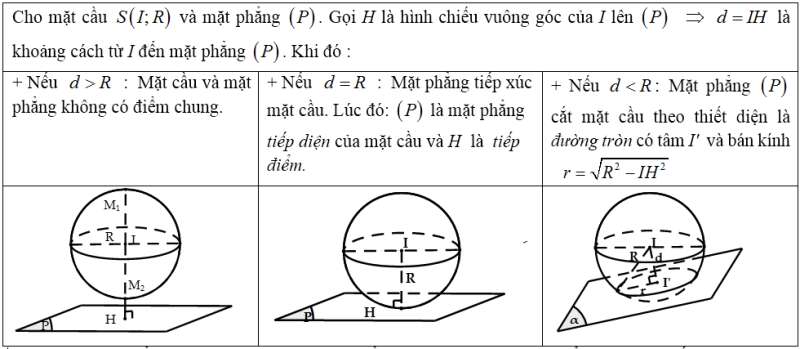
    Lưu ý: Khi mặt phẳng (P) đi qua tâm I thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.

    c) Vị trí tương đối giữa mặt cầu và đường thẳng :

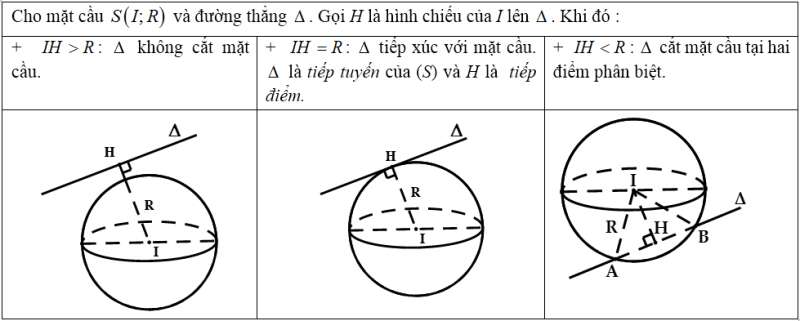
    * Lưu ý: Trong trường hợp Δ cắt (S) tại 2 điểm A, B thì bán kính R của (S) được tính như sau:

        + Xác định: d(I; Δ) = IH

        + Lúc đó: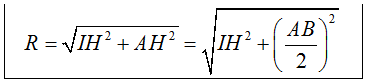

    ĐƯỜNG TRÒN TRONG KHÔNG GIAN OXYZ

    * Đường tròn (C) trong không gian Oxyz, được xem là giao tuyến của (S) và mặt phẳng .

    (S): x² + y² + z² - 2ax -2by - 2cz + d = 0

    (α): Ax + By + Cz + D = 0

    * Xác định tâm I’ và bán kính R’ của (C).

        + Tâm I' = d ∩ (α) .

    Trong đó d là đường thẳng đi qua I và vuông góc với mp(α)

        + Bán kính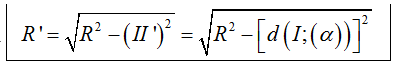 

    d) Điều kiện tiếp xúc : Cho mặt cầu (S) tâm I, bán kính R.

        + Đường thẳng Δ là tiếp tuyến của (S) ⇔ d(I; Δ) = R

        + Mặt phẳng (α) là tiếp diện của (S) ⇔ d(I;(α)) = R

    * Lưu ý: Tìm tiếp điểm M_o(x_o; y_o; z_o) .

    Sử dụng tính chất :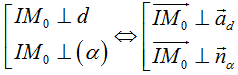

B. Bài tập trắc nghiệm

Bài 1: Cho hai điểm A(1;3;5), B(1;-1;1), khi đó trung điểm I của AB có tọa độ là:

A. I(0;-4;-4).

B. I(2;2;6).

C. I(0;-2;-4).

D. I(1;1;3).

Đáp án: D.

Ta có: 

Bài 2: Trong không gian với hệ tọa độ Oxyz, cho a→= (1;2;3), b→= (-2;3;-1). Khi đó a→+ b→có tọa độ là:

A. (-1;5;2).

B. (3;-1;4).

C. (1;5;2).

D. (1;-5;-2).

Đáp án: A.

Ta có: a→+ b→= (-1;5;2).

Bài 3: Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(5;2;0). Khi đó:

A. |AB⟶| = 5.

B. |AB⟶| = 2√3.

C. |AB⟶| = √61.

D. |AB⟶| = 3.

Đáp án: A.

Bài 4: Trong không gian với hệ tọa độ Oxyz, cho hai véctơ a→= (2;-3;1) và b→= (-1;0;4). Tìm tọa độ véctơ u→= -2a→+ 3b→.

A. u→= (-7;6;-10).

B. u→= (-7;6;10).

C. u→= (7;6;10).

D. u→= (-7;-6;10).

Đáp án: B.

Ta có -2a→+ 3b→= (-7;6;10), nên u→= (-7;6;10).

Bài 5: Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D'. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D'(6;8;10). Tọa độ điểm B' là:

A. B'(8;4;10).

B. B'(6;12;0).

C. B'(10;8;6).

D. B'(13;0;17).

Đáp án: D.

Ta có: AD⟶= BC⟶= (-5;4;-7) ⇒ D(-3;8;-7).

Lại có: BD⟶= B'D'⟶= (-7;8;-7) ⇒ B'(13;0;17).

Bài 6: Trong không gian với hệ tọa độ Oxyz, cho véc-tơ u→= (1;2;0). Mệnh đề nào sau đây là đúng?

A. u→= 2i→+ j→.

B. u→= i→+ 2j→.

C. u→= j→+ 2k→.

D. u→= i→+ 2k→.

Đáp án: B.

Ta có: u→= xi→+ yj→+ zk→ ⇔ u→= (x;y;z).

Suy ra u→= (1;2;0) ⇔ u→= i→+ 2j→.

Bài 7: Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(2;1;-1), B(3;3;1), C(4;5;3). Khẳng định nào đúng?

A. AB ⊥ AC.

B. A, B, C thẳng hàng.

C. AB = AC.

D. O, A, B, C là 4 đỉnh của một tứ diện.

Đáp án: B.

AB⟶= (1;2;2), AC⟶= (2;4;4) ⇒ AC⟶= 2AB⟶.

Vậy A,B,C thẳng hàng.

Bài 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-4;-5). Tìm tọa độ điểm A' đối xứng với A qua mặt phẳng (Oxz) là:

A. (1;-4;5).

B. (-1;4;5).

C. (1;4;5).

D. (1;4;-5).

Đáp án: D.

Dễ thấy phương trình mặt phẳng (Oxz): y = 0 nên suy ra điểm đối xứng với A(1;-4;-5) qua (Oxz) là điểm A'(1;4;-5).

Bài 9: Trong không gian Oxyz, cho véc-tơ u→sao cho u→= 2i→+ j→- 2k→. Tọa độ của véc-tơ u→là:

A. (-2;1;2).

B. (1;2;-2).

C. (2;1;-2).

D. (2;1;2).

Đáp án: C.

Tọa độ của véc-tơ u→= (2;1;-2).

Bài 10: Trong không gian với hệ tọa độ Oxyz, cho hai vec-tơ a→= (0;1;3); b→= (-2;3;1). Tìm tọa độ của vec-tơ x→biết x→= 3a→+ 2b→.

A. x→= (-2;4;4).

B. x→= (4;-3;7).

C. x→= (-4;9;11).

D. x→= (-1;9;11).

Đáp án: C.

3a→= (0;3;9); 2b→= (-4;6;2) ⇒ x→= 3a→+ 2b→= (-4;9;11).

Bài 11: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(-2;6;1) và M'(a;b;c) đối xứng nhau qua mặt phẳng (Oyz). Tính S = 7a - 2b + 2017c - 1.

A. S = 2017.

B. S = 2042.

C. S = 0.

D. S = 2018.

Đáp án: D.

Gọi H là hình chiếu của M lên (Oyz), suy ra H(0;6;1).

Do M' đối xứng với M qua (Oyz) nên MM' nhận H làm trung điểm, suy ra M'(2;6;1).

Vậy T = 7.2 - 2.6 + 2017.1 - 1 = 2018.

Bài 12: Trong hệ tọa độ Oxyz, cho OA⟶= 3k→- i→. Tìm tọa độ của điểm A.

A. (3;0;-1).

B. (-1;0;3).

C. (-1;3;0).

D. (3;-1;0).

Đáp án: B.

Ta có OA⟶= 3k→- i→= -1i→+ 0j→+ 3k→. Do đó tọa độ điểm A(-1;0;3).

Bài 13: Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với điểm A qua gốc tọa độ O là:

A. A'(3;-2;1).

B. A'(3;2;-1).

C. A'(3;-2;-1).

D. A'(3;2;1).

Đáp án: A.

Ta có x_A' = 2x_O - x_A =3; y_A' = 2y_O - y_A = -2; z_A' = 2z_O - z_A = 1. Vậy A'(3;-2;1).

Bài 14: Trong không gian với hệ tọa độ Oxyz, cho véc-tơ a→= (1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ a→?

A. c→= (2;0;-4).

B. b→= (1;0;2).

C. d→= (-1/2;0;1).

D. 0→= (0;0;0).

Đáp án: B.

Ta có 0→cùng phương với mọi véc-tơ; c→= 2a→và 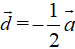 nên c→và d→cùng phương với a→.

Bài 15: Trong không gian với hệ toạ độ Oxyz, hình chiếu của điểm M(1;-3;-5) trên mặt phẳng (Oyz) có toạ độ là:

A. (0;-3;0).

B. (0;-3;-5).

C. (0;-3;5).

D. (1;-3;0).

Đáp án: B.

Phương trình mặt phẳng (Oyz) là x = 0 và hình chiếu của điểm I(a;b;c) lên mặt phẳng (Oyz) là (0;b;c).

Bài 16: Trong không gian Oxyz, cho điểm M(3;-1;2). Tìm tọa độ điểm N đối xứng với M qua mặt phẳng (Oyz).

A. N(0;-1;2).

B. N(3;1;-2).

C. N(-3;-1;2).

D. N(0;1;1).

Đáp án: C.

Lấy đối xứng qua mặt (Oyz) thì x đổi dấu còn y, z giữ nguyên nên N(-3;-1;2).

Bài 17: Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm K(0;2;2√2) và tiếp xúc với mặt phẳng (Oxy) là:

A. x² + (y - 2)² + (z - 2√2)² = 4.

B. x² + (y - 2)² + (z - 2√2)² = 8.

C. x² + (y - 2)² + (z - 2√2)² = 2√2.

D. x² + (y - 2)² + (z - 2√2)² = 2.

Đáp án: B.

Bán kính mặt cầu tâm K và tiếp xúc với (Oxy) là R = d(K,(Oxy)) = 2√2.

⇒ Phương trình mặt cầu là: x² + (y - 2)² + (z - 2√2)² = 8.

Bài 18: Trong không gian Oxyz, cho các điểm A(-1;2;-3), B(2;-1;0). Tìm tọa độ véc-tơ AB⟶.

A. AB⟶= (3;-3;-3).

B. AB⟶= (3;-3;3).

C. AB⟶= (-3;3;-3).

D. AB⟶= (1;-1;1).

Đáp án: B.

Ta có AB⟶= (2 - (-1);-1 - 2;0 - (-3)) = (3;-3;3).

Bài 19: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x + 1)² + (y - 2)² + (z - 1)² = 9. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).

A. I(-1;2;1) và R = 3.

B. I(-1;2;1) và R = 9.

C. I(1;-2;-1) và R = 3.

D. I(1;-2;-1) và R = 9.

Đáp án: A.

Mặt cầu (S) có tâm I(-1;2;1) và bán kính R = √9 = 3.

Bài 20: Trong không gian Oxyz, cho điểm A(4;2;1) và B(2;0;5). Tìm tọa độ véc-tơ AB⟶.

A. (2;2;-4).

B. (-2;-2;4).

C. (-1;-1;2).

D. (1;1;-2).

Đáp án: B.

Ta có AB⟶= (2 - 4;0 - 2;5 - 1) = (-2;-2;4).

Bài 21: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC.

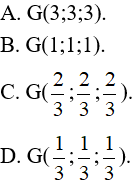
Đáp án: B.

Tọa độ trọng tâm tam giác ABC là G(1;1;1).

Bài 22: Cho a→= (2;0;1). Độ dài của véc-tơ a→bằng:

A. 5.

B. 3.

C. √5.

D. √3.

Đáp án: C.

Bài 23: Trong không gian với hệ tọa độ Oxyz, tìm tọa độ u→biết u→= 2i→- 3j→+ 5k→.

A. u→= (5;-3;2).

B. u→= (2;-3;5).

C. u→= (2;5;-3).

D. u→= (-3;5;2).

Đáp án: B.

u→= 2i→- 3j→+ 5k→ ⇒ u→= (2;-3;5).

Bài 24: Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ OA⟶= -2j→+ 3k→. Tìm tọa độ điểm A.

A. A(-2;3;0).

B. A(-2;0;3).

C. A(0;2;-3).

D. A(0;-2;3).

Đáp án: D.

Ta có OA⟶= -2j→+ 3k→= (0;-2;3) ⇒ A(0;-2;3).

Bài 25: Trong không gian Oxyz cho a→(1;-2;3); b→= 2i→- 3k→. Khi đó tọa độ a→+ b→là:

A. (3;-2;0).

B. (3;-5;-3).

C. (3;-5;0).

D. (1;2;-6).

Đáp án: A.

b→= 2i→- 3k→= (2;0;-3). Khi đó a→+ b→= (3;-2;0).

Bài 26: Trong không gian với hệ trục tọa độ Oxyz, cho hai véc-tơ a→= (1;-2;0) và b→= (-2;3;1). Khẳng định nào sau đây là sai?

A. a→.b→= -8.

B. 2a→= (2;-4;0).

C. a→+ b→= (-1;1;-1).

D. |b→| = √14.

Đáp án: C.

Ta có a→+ b→= (-1;1;1).

Bài 27: Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(-4;4;6). Tọa độ trọng tâm G của tam giác OAB là:

A. G(1;-2;-3).

B. G(-1;2;3).

C. G(-3;6;9).

D. G(-3/2;3;9/2).

Đáp án: B.

Giả sử G(x_G;y_G;z_G).

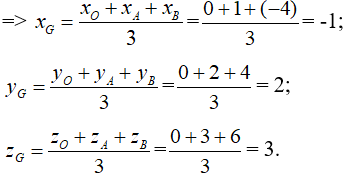
Vậy G(-1;2;3).

Bài 28: Trong không gian với hệ tọa độ Oxyz, cho a→= (1;-1;3), b→= (2;0;-1). Tìm tọa độ véc-tơ u→= 2a→- 3b→.

A. u→= (4;2;-9).

B. u→= (-4;-2;9).

C. u→= (1;3;-11).

D. u→= (-4;-5;9).

Đáp án: B.

u→= 2a→- 3b→= (-4;-2;9).

Bài 29: Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:

A. H(0;-1;0).

B. H(0;-1;4).

C. H(2;-1;0).

D. H(2;0;4).

Đáp án: C.

Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

Bài 30: Trong không gian Oxyz, cho điểm A thỏa mãn OA⟶= 2i→- 3j→+ 7k→. Khi đó tọa độ điểm A là:

A. (-2;3;7).

B. (2;-3;7).

C. (-3;2;7).

D. (2;7;-3).

Đáp án: B.

Ta có i→= (1;0;0), j→= (0;1;0), k→= (0;0;1). Vậy OA⟶= 2i→- 3j→+ 7k→= (2;-3;7).

Bài 31: Trong không gian Oxyz, cho hai điểm A(5;1;3), H(3;-3;-1). Tọa độ của điểm A' đối xứng với A qua H là:

A. (-1;7;5).

B. (1;7;5).

C. (1;-7;-5).

D. (1;-7;5).

Đáp án: C.

Do A' đối xứng với A qua H nên AA' nhận H làm trung điểm.

⇒ x_A' = 2x_H - x_A = 1; y_A' = 2y_H - y_A = -7; z_A' = 2z_H - z_A = -5.

Bài 32: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(5;7;2), B(3;0;4). Tọa độ của AB⟶là:

A. AB⟶= (2;7;-2).

B. AB⟶= (2;7;2).

C. AB⟶= (8;7;6).

D. AB⟶= (-2;-7;2).

Đáp án: D.

Ta có AB⟶= (-2;-7;2).

Bài 33: Trong không gian Oxyz, cho điểm M(-2;5;1). Khoảng cách từ M đến trục Ox bằng:

A. √29.

B. 2.

C. √5.

D. √26.

Đáp án: D.

Bài 34: Trong không gian toạ độ Oxyz, cho điểm A(2;4;3). Khoảng cách từ điểm A đến mặt phẳng (Oyz) là:

A. 2.

B. 4.

C. 3.

D. 5.

Đáp án: A.

Hình chiếu của điểm A xuống mặt phẳng (Oyz) là H(0;4;3) nên khoảng cách từ điểm A đến mặt phẳng (Oyz) là AH = 2.

Bài 35: Trong không gian Oxyz, cho hai véc-tơ a→= (2;0;-1) và b→= (3;-2;1). Tìm tọa độ véc-tơ u→= 2a→- b→.

A. u→= (1;2;-3).

B. u→= (-4;4;-3).

C. u→= (5;-2;-1).

D. u→= (7;-2;-1).

Đáp án: A.

u→= 2a→- b→= 2(2;0;-1) - (3;-2;1) = (1;2;-3).

Bài 36: Trong không gian Oxyz, cho hai véc-tơ u→= i→√3 + k→và v→= j→√3 + k→. Khi đó tích vô hướng của u→.v→bằng:

A. 2.

B. 1.

C. -3.

D. 3.

Đáp án: B.

Do giả thiết nên u→(√3;0;1) và v→(0;√3;1). Khi đó u→.v→= √3.0 + 0.√3 + 1.1 = 1.

Bài 37: Trong không gian Oxyz, cho điểm M(1;0;2). Mệnh đề nào sau đây đúng?

A. M ∈ (Oxz).

B. M ∈ (Oyz).

C. M ∈ Oy.

D. M ∈ (Oxy).

Đáp án: A.

Mọi điểm có thành phần tung độ bằng 0 đều thuộc mặt phẳng (Oxz). Do đó điểm M(1;0;2) thuộc mặt phẳng (Oxz).

Bài 38: Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a→= (3;2;1), b→= (-2;0;1). Độ dài của véc-tơ a→+ b→bằng:

A. 1.

B. 2.

C. 3.

D. √2.

Đáp án: C.

a→+ b→= (3+(-2);2+0;1+1) = (1;2;2), nên:

Bài 39: Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a→= (2;4;-2) và b→= (3;-1;6). Tính giá trị của P = a→.b→.

A. P = -10.

B. P = -40.

C. P = 16.

D. P = -34.

Đáp án: A.

Ta có a→.b→= 2.3 + 4.(-1) + (-2).6 = -10.

Bài 40: Cho ba điểm A(2;1;4), B(2;2;-6), C(6;0;-1). Tích vô hướng của AB⟶.AC⟶có giá trị bằng:

A. -51.

B. 51.

C. 55.

D. 49.

Đáp án: D.

AB⟶= (0;1;-10), AC⟶= (4;-1;-5), AB⟶.AC⟶= 49.

Bài 41: Trong không gian với hệ trục tọa độ Oxyz, cho hai véc-tơ u→= (1;2;3) và v→= (-5;1;1). Khẳng định nào đúng?

A. u→= v→.

B. u→⊥ v→.

C. |u→|= |v→|.

D. u→|| v→.

Đáp án: B.

u→.v→= 1.(-5) + 2.1 + 3.1 = 0 ⇒ u→⊥ v→.

Bài 42: Trong không gian với hệ tọa độ Oxyz, cho véc-tơ u→= (x;2;1) và véc-tơ v→= (1;-1;2x). Tính tích vô hướng của u→và v→.

A. x + 2.

B. 3x - 2.

C. 3x + 2.

D. - 2 - x.

Đáp án: B.

Ta có u→.v→= x - 2 + 2x = 3x - 2.

Bài 43: Cho ba điểm A(2;1;4), B(-2;2;-6), C(6;0;-1). Tích AB⟶. AC⟶bằng:

A. -67.

B. 65.

C. 33.

D. 67.

Đáp án: C.

Ta có AB⟶= (-4;1;-10) và AC⟶= (4;-1;-5). Khi đó tích vô hướng AB⟶. AC⟶= 33.

Bài 44: Trong không gian với hệ toạ độ Oxyz, cho ba véc-tơ a→= (-1;1;0), b→= (1;1;0) và c→= (1;1;1). Mệnh đề nào dưới đây sai?

A. c→⊥ b→.

B. | c→| = √3.

C. a→⊥ b→.

D. | a→| = √2.

Đáp án: A.

Ta có c→.b→= 1.1 + 1.1 + 1.0 = 2 ≠ 0 nên mệnh đề c→⊥ b→là sai.

Bài 45: Trong không gian Oxyz, cho hai véc-tơ u→= (1;-3;4) và v→= (1;3;0). Tính u→.v→.

A. (1;-3;4).

B. -8.

C. -5.

D. (1;-9;0).

Đáp án: B.

Ta có u→.v→= 1.1 + (-3).3 + 4.0 = -8.

Bài 46: Trong không gian với hệ tọa độ Oxyz cho u→= (1;0;1), v→= (0;1;-2). Tích vô hướng của u→và v→là:

A. u→. v→= -2.

B. u→. v→= 2.

C. u→. v→= (0;0;-2).

D. u→. v→= 0.

Đáp án: A.

Ta có u→. v→= 1.0 + 0.1 + 1.(-2) = -2.

Bài 47: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 5)² + (y - 1)² + (z + 2)² = 9. Tính bán kính R của mặt cầu (S).

A. R = 18.

B. R = 9.

C. R = 3.

D. R = 6.

Đáp án: C.

Mặt cầu (S) có tâm I(a; b; c) và bán kính R thì có phương trình (x - a)² + (y - b)² + (z - c)² = R².

Theo đề bài ta có R² = 9 ⇒ R = 3.

Bài 48: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x² + y² + z² + 2x - 4y + 6z - 2 = 0. Tìm tọa độ tâm I và tính bán kính R của (S).

A. Tâm I(-1;2;-3) và bán kính R = 4.

B. Tâm I(1;-2;3) và bán kính R = 4.

C. Tâm I(-1;2;3) và bán kính R = 4.

D. Tâm I(1;-2;3) và bán kính R = 16.

Đáp án: A.

Ta có (S): (x + 1)² + (y - 2)² + (z + 3)² = 16.

Do đó mặt cầu (S) có tâm I(-1;2;-3) và bán kính R = 4.

Bài 49: Trong không gian Oxyz, cho mặt cầu (S): (x - 1)² + (y + 2)² + z² = 25. Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

A. I(1;-2;0), R = 5.

B. I(-1;2;0), R = 25.

C. I(1;-2;0), R = 25.

D. I(-1;2;0), R = 5.

Đáp án: A.

Mặt cầu (S): (x - a)² + (y - b)² + (z - c)² = R² có tâm là I(a;b;c) và bán kính là R.

Do đó, mặt cầu (S): (x - 1)² + (y + 2)² + z² = 25 có tâm I(1;-2;0) và bán kính R = 5.

Bài 50: Trong không gian Oxyz, phương trình mặt cầu tâm I(2;1;-3) bán kính R = 4 là:

A. (x + 2)² + (y + 1)² + (z - 3)² = 16.

B. (x + 2)² + (y + 1)² + (z - 3)² = 4.

C. (x - 2)² + (y - 1)² + (z + 3)² = 4.

D. (x - 2)² + (y - 1)² + (z + 3)² = 16.

Đáp án: D.

Áp dụng công thức mặt cầu tâm I(a;b;c), bán kính R có phương trình là (x - a)² + (y - b)² + (z - c)² = R².