Phương trình mặt phẳng (Lý thuyết + 50 bài tập có lời giải)

A. Tóm tắt lý thuyết

I. Vectơ pháp tuyến của mặt phẳng

    • Vectơ n→ ≠ 0→ là vectơ pháp tuyến (VTPT) nếu giá của n→ vuông góc với mặt phẳng (α)

    • Chú ý:

    - Nếu n→ là một VTPT của mặt phẳng (α) thì kn→ cũng là một VTPT của mặt phẳng (α).

    - Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.

    - Nếu u→, v→ có giá song song hoặc nằm trên mặt phẳng (α) thì n→ = [u→, v→] là một VTPT của (α)

II. Phương trình tổng quát của mặt phẳng

    - Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:

    Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0

    - Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).

    - Phương trình mặt phẳng đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - x_o) + B(y - y_o) + C(z - z_o) = 0 .

    • Các trường hợp riêng

    Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0

    - Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.

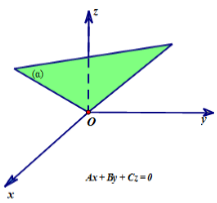
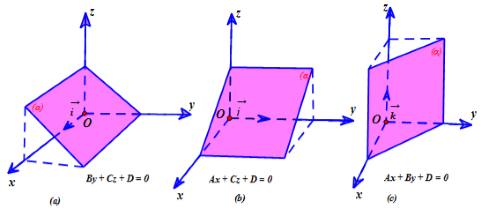
    - Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.

    - Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.

    - Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.

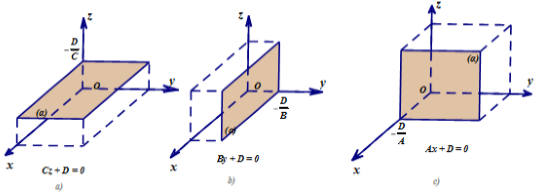
    - Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).

    - Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).

    - Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).

    Chú ý:

    - Nếu trong phương trình (α) không chứa ẩn nào thì (α) song song hoặc chứa trục tương ứng.

    - Phương trình mặt phẳng theo đoạn chắn (α): . Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0), (0; b; 0), (0; 0; c) với abc ≠ 0.

III. Khoảng cách từ một điểm đến một mặt phẳng.

    • Trong không gian Oxyz, cho điểm M_o(x_o; y_o; z_o) và mặt phẳng (α): Ax + By + Cz + D = 0

    Khi đó khoảng cách từ điểm M_o đến mặt phẳng (α) được tính:

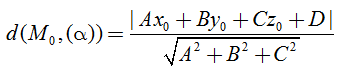
IV. Góc giữa hai mặt phẳng

    Trong không gian Oxyz, cho hai mặt phẳng (α): A₁x + B₁y + C₁z + D₁ = 0 và (β): A₂x + B₂y + C₂z + D₂ = 0

    Góc giữa (α) và (β) bằng hoặc bù với góc giữa hai VTPT n_α→, n_β→. Tức là:

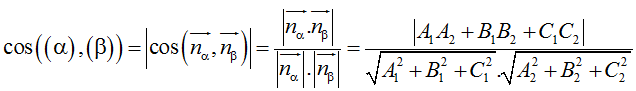
B. Bài tập trắc nghiệm